一、01背包问题
题目
有N件物品和一个容量为V的背包。第i件物品的费用是c[i],价值是w[i]。求解将哪些物
品装入背包可使价值总和最大。
基本思路
这是最基础的背包问题,特点是:每种物品仅有一件,可以选择放或不放。
用子问题定义状态:即f[i][v]表示前i件物品恰放入一个容量为v的背包可以获得的最大价值。
则其状态转移方程便是:
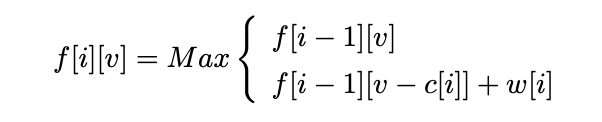
这个方程非常重要,基本上所有跟背包相关的问题的方程都是由它衍生出来的。所以有必要将它详细解释一下:“将前i件物品放入容量为v的背包中”这个子问题。
若只考虑第i件物品的策略(放或不放),那么就可以转化为一个只牵扯前i-1件物品的问题。
- 如果不放第i件物品,那么问题就转化为“前i-1件物品放入容量为v的背包中”,价值为f[i-1][v];
- 如果放第i件物品,那么问题就转化为“前i-1件物品放入剩下的容量为v-c[i]的背包中”,此时能获得的最大价值就是f[i-1][v-c[i]]再加上通过放入第i件物品获得的价值w[i]。
def bag(n, V, c, w):
"""
01背包问题的二维动态规划
args:
n: 物品的数量
V : 书包能承受的重量,
c: 每个物品的重量,例如 c= [2, 2, 3, 1, 5, 2]
w :每个物品的价值,例如w = [2, 3, 1, 5, 4, 3]
return:
f: 返回最大价值矩阵
"""
# 首先初始化价值矩阵
f = [[0 for i in range(V+1)] for j in range(n+1)]
for i in range(1,n+1):
for j in range(1,V+1):
if j >= c[i-1]:
f[i][j] = max(f[i-1][j],w[i-1]+f[i-1][j-c[i-1]])
else:
f[i][j] = f[i-1][j]
return f
n = 6
V = 10
c = [2, 2, 3, 1, 5, 2]
w = [2, 3, 1, 5, 4, 3]
value = bag(n, V, c, w)
value
[[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
[0, 0, 2, 2, 2, 2, 2, 2, 2, 2, 2],
[0, 0, 3, 3, 5, 5, 5, 5, 5, 5, 5],
[0, 0, 3, 3, 5, 5, 5, 6, 6, 6, 6],
[0, 5, 5, 8, 8, 10, 10, 10, 11, 11, 11],
[0, 5, 5, 8, 8, 10, 10, 10, 12, 12, 14],
[0, 5, 5, 8, 8, 11, 11, 13, 13, 13, 15]]
输出背包所放的物品
思路:只需从尾遍历物品,当f[i][v]大于f[i-1][v]时,表示第i个物品被放进了背包。
def show(n, V, c, value):
out = []
v = V
for i in range(n,0,-1):
if value[i][v] > value[i-1][v]:
out.append(i)
v -= c[i-1]
return out[::-1]
n = 6
V = 10
c = [2, 2, 3, 1, 5, 2]
w = [2, 3, 1, 5, 4, 3]
value = bag(n, V, c, w)
out = show(n, V, c, value)
print(out)
[2, 4, 5, 6]
优化空间复杂度
以上方法的时间和空间复杂度均为Θ(V*N),其中时间复杂度应该已经不能再优化了,但空间复杂度却可以优化到Θ(V)。
由于从状态转移方程来看,f[i][v]是由f[i-1][v]和f[i-1][v-c[i]]两个子问题递推而来。 也就是说,第i行的值只与第i-1行的值有关。
所以可以只用一个数组f[0..V],定义第i行的状态值。
更新第i行前,f[0..V]存的是i-1行的价值,更新第i行后f[0..V]存i行的价值。两者存在一个数组里,更新过程中第i行的f[v]会逐渐把第i-1行的f[v]覆盖。
因为求第i行的f[v]需要由第i-1行的f[v - w[i]]值递推,若顺序遍历,求第i行的f[v]时,第i-1行的f[v - w[i]]值就已被覆盖。
为了避免这种情况,我们使用逆序遍历,此时f[v]则变成从尾部开始覆盖,则满足计算需求。
def bag(n, V, c, w):
"""
01背包问题的一维动态规划
args:
n: 物品的数量
V : 书包能承受的重量,
c: 每个物品的重量,例如 c= [2, 2, 3, 1, 5, 2]
w :每个物品的价值,例如w = [2, 3, 1, 5, 4, 3]
return:
f: 返回最大价值矩阵
"""
# 首先初始化价值矩阵
f = [0 for i in range(V+1)]
for i in range(1,n+1):
for j in range(V,0,-1):
if j >= c[i-1]:
f[j] = max(f[j],w[i-1]+f[j-c[i-1]])
return f
n = 6
V = 10
c = [2, 2, 3, 1, 5, 2]
w = [2, 3, 1, 5, 4, 3]
value = bag(n, V, c, w)
value
[0, 5, 5, 8, 8, 11, 11, 13, 13, 13, 15]
二、完全背包问题
题目
有N种物品和一个容量为V的背包,每种物品都有无限件可用。第i种物品的费用是c[i],
价值是w[i]。求解将哪些物品装入背包可使这些物品的费用总和不超过背包容量,且价值总和最
大。
解法1
这个问题非常类似于01背包问题,所不同的是每种物品有无限件。也就是从每种物品的角度考虑,与它相关的策略已并非取或不取两种,而是有取0件、取1件、取2件……等很多种。
如果仍然按照解01背包时的思路,令f[i][v]表示前i种物品恰放入一个容量为v的背包的最大权值。仍然可以按照每种物品不同的策略写出状态转移方程,像这样:
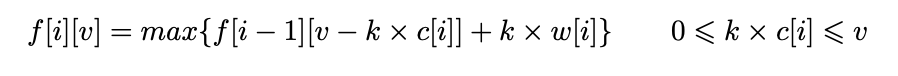
这跟01背包问题一样有O(VN)个状态需要求解,但求解每个状态的时间已经不是常数了,求解状态f[i][v]的时间是Θ(V/c[i]),总的复杂度可以认为是Θ(V ×∑ V/c[i]),是比较大的。因此可以去改进这个复杂度。
解法2
只需要基于 0-1背包问题的一维DP解法修改一行代码即可!!! 即把计算f[v]的逆序遍历改为顺序遍历即可。原因如下:
首先想想为什么P01中要按照v=V..0的逆序来循环。这是因为要保证第i次循环中的状态f[i][v]是由状态f[i-1][v-c[i]]递推而来。换句话说,这正是为了保证每件物品只选一次,保证在考虑“选入第i件物品”这件策略时,依据的是一个绝无已经选入第i件物品的子结果f[i-1][v-c[i]]。
而现在完全背包的特点恰是每种物品可选无限件,所以在考虑“加选一件第i种物品”这种策略时,却正需要一个可能已选入第i种物品的子结果f[i][v-c[i]],所以就可以并且必须采用v=0..V的顺序循环。这就是这个简单的程序为何成立的道理。
对应的状态转移方程为:
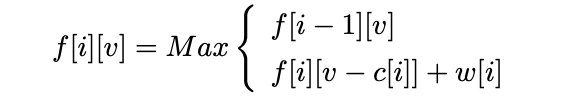
该算法时间复杂度:O(VN)
def bag(n, V, c, w):
"""
完全背包问题的一维动态规划
args:
n: 物品的数量
V : 书包能承受的重量,
c: 每个物品的重量,例如 c= [2, 2, 3, 1, 5, 2]
w :每个物品的价值,例如w = [2, 3, 1, 5, 4, 3]
return:
f: 返回最大价值矩阵
"""
# 首先初始化价值矩阵
f = [0 for i in range(V+1)]
for i in range(1,n+1):
for j in range(1,V+1):
if j >= c[i-1]:
f[j] = max(f[j],w[i-1]+f[j-c[i-1]])
return f
n = 6
V = 10
c = [2, 2, 3, 1, 5, 2]
w = [2, 3, 1, 5, 4, 3]
value = bag(n, V, c, w)
value
[0, 5, 10, 15, 20, 25, 30, 35, 40, 45, 50]
三、多重背包问题
题目
有N种物品和一个容量为V的背包。第i种物品最多有n[i]件可用,每件费用是c[i],价值
是w[i]。求解将哪些物品装入背包可使这些物品的费用总和不超过背包容量,且价值总和最大。
解法1
这题目和完全背包问题很类似。基本的方程只需将完全背包问题的方程略微一改
即可,因为对于第i种物品有n[i]+1种策略:取0件,取1件. . .取n[i]件。令f[i][v]表示前i种物品恰放
入一个容量为v的背包的最大权值,则有状态转移方程如下,复杂度是(V ×∑n[i])。
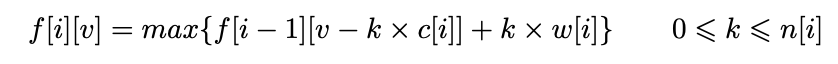
def bag(n, V, c, w, s):
"""
完全背包问题的一维动态规划
args:
n: 物品的数量
V : 书包能承受的重量,
c: 每个物品的重量,例如 c= [2, 2, 3, 1, 5, 2]
w :每个物品的价值,例如w = [2, 3, 1, 5, 4, 3]
return:
f: 返回最大价值矩阵
"""
# 首先初始化价值矩阵
f = [0 for i in range(V+1)]
for i in range(1,n+1):
for j in range(1,V+1):
for k in range(s[i-1]+1):
if j >= k*c[i-1]:
f[j] = max(f[j],k*w[i-1]+f[j-k*c[i-1]])
return f
n = 6
V = 10
c = [2, 2, 3, 1, 5, 2]
w = [2, 3, 1, 5, 4, 3]
s = [2, 3, 1, 4, 5, 3]
value = bag(n, V, c,w, s)
value
[0, 5, 10, 15, 20, 25, 30, 35, 40, 45, 50]
参考链接:
背包九讲:https://comzyh.com/upload/PDF/Pack-PDF-Comzyh.pdf
背包问题及其变型(python):https://blog.csdn.net/qq_22526061/article/details/83504116