处理何种问题:凸包可以看成在木板上钉许多钉子,用一根橡皮筋框住所有钉子所得到的多边形,最终能求得都由哪些钉子构成该凸包。如下图所示:
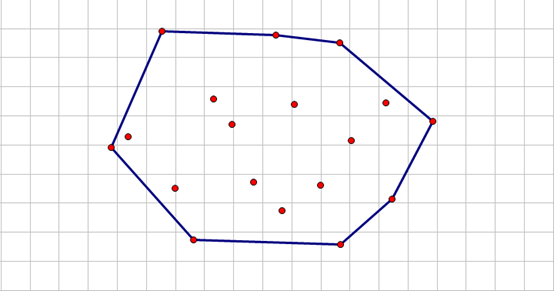
性能:由一个快排(O(nlogn))和一个遍历找点(O(n)),总体时间复杂度为O(nlogn)。
原理:
点:A(x1,y1),B(x2,y2)
向量AB=(x2-x1,y2-y1)=(x,y)
向量的叉积:a X b =
通过结果的正负判断两矢量之间的顺逆时针关系
l 若a X b > 0,表示a在b的顺时针方向上
l 若a X b < 0,表示a在b的逆时针方向上
l 若a X b == 0,表示a与b共线,但不确定方向是否相同
例如:
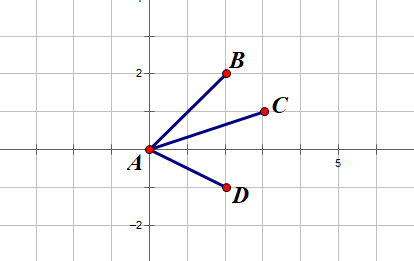
A(0,0)
B(2,2)
C(3,1)
D(2,-1)
AB(2,2),AC(3,1),AD(2,-1)
AC X AB = 3*2-1*2 = 4>0
AC在AB的顺时针方向上,即点C在向量AB的下面。
实现步骤:
- 排序:按照x由小到大排序,如果x相同,按照y由小到大排序。
- 排序之后第一个点必为凸包上的点(证明自己意淫一下,有x最大、x最小、y最小、y最大的点都必在凸包上)。
- 选最近两个刚入凸包的点,再在排序中依次选点,根据上面所提及到的原理,判断该点在凸包那两点的顺时针还是逆时针方向。
- 如果在逆时针方向,将该点加入凸包,否则判定出之前进入凸包的点不合格,删除该凸包点,重复第三步,直到该点加入凸包(也就是说每个点都曾进过凸包,只是后来有些被删了)。
- 以上就是下凸包的构成步骤,上凸包参考下凸包,基本没有什么差别,因为在判断时是判断是否为逆时针,别误以为是在判段该点在向量的下方,上凸包就不可用了,对于逆时针而言都是一样的。
- 这种方法求出来的点是凸包沿着逆时针方向找出来的,首位相接且第一个点重复两次,所以除了点只有一个的情况下,记得点的个数减一。
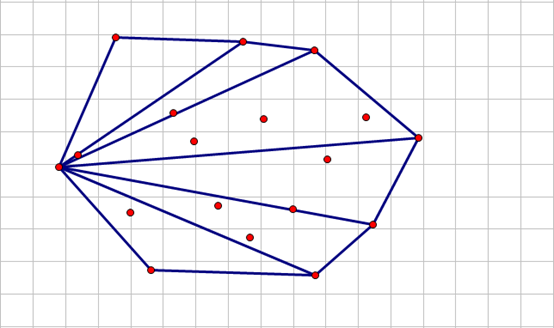
备注:对于题目要求求凸包构成的面积时,可以参考以下图示求法:
输入样例解释:
11---散点样例个数
5 8 ---散点坐标
12 56
5 2
125 1
15 66
45 77
55 6
45 2
232 5
45 12
54 66
输出样例解释:
tot=7 ---构成凸包点的个数
1: 5.00 , 2.00 ---沿着凸包逆时针方向,且保留两位小数
2: 125.00 , 1.00
3: 232.00 , 5.00
4: 45.00 , 77.00
5: 15.00 , 66.00
6: 12.00 , 56.00
7: 5.00 , 8.00
--------------------------------------------------------------------------------------------
实现代码
1 //求凸包,时间复杂度nlogn 2 #include<iostream> 3 #include<cstdio> 4 #include<algorithm> 5 #include<cmath> 6 #include<cstring> 7 using namespace std; 8 9 const int MaxN=10010; 10 11 int n,tot;//n为点的个数,tot为凸点的个数 12 struct point 13 { 14 double x,y; 15 }; 16 point p[MaxN],CHP[MaxN];//CHP为凸包最后所构成的点 17 18 bool cmp(point a,point b)//水平排序,按x从大到小排,如果x相同,按y从大到小排序 19 { 20 return (a.x<b.x||(a.x==b.x&&a.y<b.y)); 21 } 22 23 double xmul(point a,point b,point c)//叉积 24 { 25 return (b.x-a.x)*(c.y-a.y)-(b.y-a.y)*(c.x-a.x); 26 } 27 28 void Andrew() 29 { 30 sort(p,p+n,cmp); 31 tot=0; 32 33 for(int i=0;i<n;++i)//计算下半个凸包 34 { 35 while(tot>1&&xmul(CHP[tot-2],CHP[tot-1],p[i])<0) 36 --tot; 37 CHP[tot++]=p[i]; 38 } 39 40 int k=tot; 41 for(int i=n-2;i>=0;--i)//计算上半个凸包 42 { 43 while(tot>k&&xmul(CHP[tot-2],CHP[tot-1],p[i])<0) 44 --tot; 45 CHP[tot++]=p[i]; 46 } 47 48 if(n>1)//对于只有一个点的包再单独判断 49 --tot; 50 } 51 52 53 int main() 54 { 55 scanf("%d",&n); 56 for(int i=0;i<n;++i) 57 { 58 scanf("%lf%lf",&p[i].x,&p[i].y); 59 } 60 Andrew(); 61 printf("tot=%d ",tot); 62 for(int i=0;i<tot;++i) 63 { 64 printf("%d: %.2lf , %.2lf ",i+1,CHP[i].x,CHP[i].y); 65 } 66 return 0; 67 }
一些预备知识点:
首先在二维坐标下介绍一些定义:
点:A(x1,y1),B(x2,y2)
向量:向量AB=( x2 - x1 , y2 - y1 )= ( x , y );
向量的模 |AB| = sqrt ( x*x+y*y );
向量的点积: 结果为 x1*x2 + y1*y2。
点积的结果是一个数值。
点积的集合意义:我们以向量 a 向向量 b 做垂线,则 | a | * cos(a,b)为 a 在向量 b 上的投影,即点积是一个向量在另一个向量上的投影乘以另一个向量。且满足交换律
应用:可以根据集合意义求两向量的夹角,
cos(a,b) =( 向量a * 向量b ) / (| a | * | b |) = (x1*x2 + y1*y2) / (| a | * | b |)
向量的叉积: 结果为 x1*y2-x2*y1
叉积的结果也是一个向量,是垂直于向量a,b所形成的平面,如果看成三维坐标的话是在 z 轴上,上面结果是它的模。
方向判定:右手定则,(右手半握,大拇指垂直向上,四指右向量a握向b,大拇指的方向就是叉积的方向)
叉积的集合意义:1:其结果是a和b为相邻边形成平行四边形的面积。
2:结果有正有负,有sin(a,b)可知和其夹角有关,夹角大于180°为负值。
3:叉积不满足交换律
应用:
1:通过结果的正负判断两矢量之间的顺逆时针关系
若 a x b > 0表示a在b的顺时针方向上
若 a x b < 0表示a在b的逆时针方向上
若 a x b == 0表示a在b共线,但不确定方向是否相同