题目描述
给出正整数n和k,计算G(n, k)=k mod 1 + k mod 2 + k mod 3 + … + k mod n的值,其中k mod i表示k除以i的余数。例如G(10, 5)=5 mod 1 + 5 mod 2 + 5 mod 3 + 5 mod 4 + 5 mod 5 …… + 5 mod 10=0+1+2+1+0+5+5+5+5+5=29
输入输出格式
输入格式:
两个整数n k
输出格式:
答案
输入输出样例
说明
30%: n,k <= 1000
60%: n,k <= 10^6
100% n,k <= 10^9
------------------------------------------------------------------------------------------------------------------------
题外话:考试头一天在lydrainbowcat的书上刚看到这道题,结果弱弱的我就打了一个小小的问号就看下一页了然后考场上就没有然后了????
进入正题
首先不难看出:
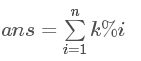
因为
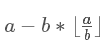
所以原式可以化简为:
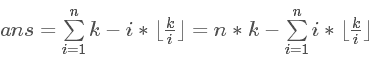
根据手推数据,我们可以发现规律:总有一段连续的i值可以使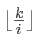 相等,所以计算这一段和的时候 可以用等差数列公式。
相等,所以计算这一段和的时候 可以用等差数列公式。
因此,我们用l和r记录每次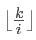 相等的左右端点,不考虑边界的情况,r=k/(k/l) 【“除得越少,剩得越多”——仔细领悟】
相等的左右端点,不考虑边界的情况,r=k/(k/l) 【“除得越少,剩得越多”——仔细领悟】
最后就是要注意一下边界,r=min(k/(k/l),n);
然后我们就可以开始写代码了。

1 #include<iostream> 2 #include<cstdio> 3 #include<algorithm> 4 #define ll long long 5 using namespace std; 6 int main() 7 { 8 ll n,k; 9 scanf("%lld%lld",&n,&k); 10 ll ans=n*k; 11 for(ll l=1,r;l<=n;l=r+1) 12 { 13 //cout<<l<<" "; 14 if(k/l!=0) 15 { 16 r=min(k/(k/l),n); 17 //cout<<k/(k/l)<<" "<<n<<endl; 18 } 19 else r=n; 20 ans-=(k/l)*(r-l+1)*(l+r)/2; 21 } 22 printf("%lld",ans); 23 return 0; 24 }
