题目描述
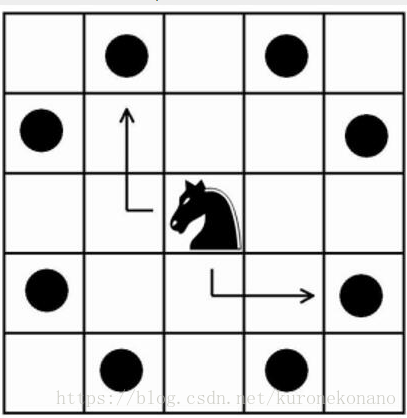
一个骑士在一个无限大的国际象棋棋盘里跳。一开始,这个国际象棋棋盘的每一个格子都是被标记为未被走过的,而骑士一开始可以以任意的一个格子作为起点,并且这个格子标记为走过。然后,他可以以如下图的规则跳N次,每一个他所到过的格子都会被标记为已经走过。
现在,我们需要知道在N次跳跃之后,有多少个格子可能被标记为走过。
输入
第一行一个整数T,表示数据组数
接下来T行,每行一个整数N
输出
共T行,每行一个整数,表示对应测试数据的答案
样例输入
3
0
1
7
样例输出
1
9
649
提示
对于30%的数据,1<=T<=10,N<=1,000
对于60%的数据,1<=T<=100,N<=1,000,000
对于100%的数据,1<=T<=100,000,N<=1,000,000,000
首先这题真的真的很恶心,1e9的数据,无计可施的我只能认为是打表找规律。
首先先广搜,输出前100项数据。
以下是模拟的广搜代码:
#include<stdio.h>
#include<string.h>
#include<queue>
using namespace std;
bool vis[2002][2002];
int walkx[]= {1,2,1,2,-1,-2,-1,-2};
int walky[]= {-2,-1,2,1,2,1,-2,-1};
struct point
{
int x,y,num;
};
int main()
{
queue<point>q;
int llst=0;
int last=0;
for(int i=0; i<=10; i++)
{
int n=i;
memset(vis,false,sizeof(vis));
while(!q.empty())q.pop();
point st;
st.x=1000;
st.y=1000;
st.num=0;
vis[st.x][st.y]=true;
int sum=0;
q.push(st);
while(!q.empty())
{
point top=q.front();
q.pop();
sum++;
for(int i=0; i<8; i++)
{
point tmp;
tmp.x=top.x+walkx[i];
tmp.y=top.y+walky[i];
tmp.num=top.num+1;
if(tmp.x>=0&&tmp.x<2000&&tmp.y<2000&&tmp.x>=0&&!vis[tmp.x][tmp.y]&&tmp.num<=n)
{
vis[tmp.x][tmp.y]=true;
q.push(tmp);
}
}
}
// for(int k=0; k<=100; k++)
// {
// for(int j=0; j<=100; j++)
// printf("%d",vis[k][j]);
// printf("
");
// }
printf("%d------->%d-------->%d-------->%d
",i,sum,sum-last,sum-last-llst);
llst=sum-last;
last=sum;
// printf("======%d
",llst);
}
}
第0步到第n步的所有步数在你成功敲完广搜输出之后。你会发现,这特么根本没有什么规律,接着你可能会凭着直觉输出两两数据间的差值,也就是增量。
你会发现特么仍然不是一个定值。。。
如果光看前5项,那么增量的增量仍然是变化的,况且看到增量没有规律谁特么还会去看增量的增量是否为定值,但是第五项之后,增量的增量确实为28的定值了!
0——->1——–>1——–>1
1——->9——–>8——–>7
2——->41——–>32——–>24
3——->109——–>68——–>36
4——->205——–>96——–>28
5——->325——–>120——–>24
6——->473——–>148——–>28
7——->649——–>176——–>28
8——->853——–>204——–>28
9——->1085——–>232——–>28
10——->1345——–>260——–>28
于是到此就结束了广搜的找规律过程,拿到规律开始推式子,我们将ans原数列设为a,将增量设为数列b,因为前5项是无规律的,直接打表特判。
从第五项开始有规律,那么此处作为我们推等差数列的首项。a1=325,而此处首项的增量是120,但a作为一个首项是没有增量的,因此数列b的首项是148,b1=148
在数列b中,是一个简单的等差数列,公差为28,由等差数列公式得到b【n】=120+28*n
再看数列a,我们可以得到:
a【1】=325
a【2】-a【1】=b【1】
a【3】-a【2】=b【2】
a【4】-a【3】=b【3】
a【5】-a【4】=b【4】
………
a【n】-a【n-1】=b【n-1】
将这些数列求和可以消去中间值,那么即
a【2】-a【1】+a【3】-a【2】+a【4】-a【3】+a【5】-a【4】+…….+a【n】-a【n-1】=b【1】+b【2】+b【3】+b【4】+…….+b【n-1】
化简后得: a【n】-a【1】=∑(b【1】~b【n-1】)
我们要求解a【n】=∑(b【1】~b【n-1】)+a【1】
其中b【n-1】=120+28*(n-1)
根据等差数列求和公式数列b的求和:
∑b(【1】~b【n-1】)=(n-1)*(b【1】+b【n-1】)/2
代入可得 a【n】= (n-1)*(120+28*n+120)/2+325
直接计算即可。
但是你以为这样就完了吗?
在你还在对你的推导产生怀疑的时候。这么交上去如果错了怕不是直接回到第一步开始查错。
然而只是结果爆了long long 得用unsigned long long
到此你以为就完事了?
如果你在计算公式时是直接一套公式敲上去的,还有可能在计算过程中爆掉unsigned long long
因此可以对计算改变先后顺序,先除2再乘n-1,这样才能得到最终结果
注意首项是从第五项开始,因此还需要对n处理,减去4才是通项公式中实际的n
说白了就是一道靠打表找规律再根据数列推导公式的数学题,还有各种坑点,然而,有人能证明为什么是这样一个结果吗?
#include<stdio.h>
#define ULL unsigned long long
int main()
{
ULL n,t;
ULL a[]={1,9,41,109,205};
scanf("%llu",&t);
while(t--)
{
scanf("%llu",&n);
if(n<5)
{
printf("%llu
",a[n]);
continue;
}
else
{
n-=4;
ULL ans=(240+28*n)/2*(n-1)+325;
printf("%llu
",ans);
}
}
}