本篇学习笔记内容为图的各项性质、图的表示方法、图ADT的python实现
图(Graph)
是数据结构和算法学中最强大的框架之一(或许没有之一)。图几乎可以用来表现所有类型的结构或系统,从交通网络到通信网络,从下棋游戏到最优流程,从任务分配到人际交互网络,图都有广阔的用武之地。
我们会把图视为一种由“顶点”组成的抽象网络,网络中的各顶点可以通过“边”实现彼此的连接,表示两顶点有关联。我们要知道最基础最基本的2个概念,顶点(vertex)和边(edge)。
图可以分为有向图和无向图,一般用
G=(V,E)来表示图。经常用邻接矩阵或者邻接表来描述一副图。首先是链表、树与图的对比图:
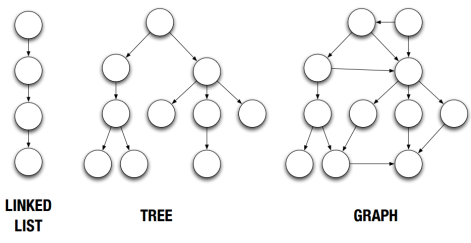
圆为顶点、线为边
图的术语

图 G 是顶点V 和边 E的集合
两个顶点之间:边
如果顶点 x 和 y 共享边,则它们相邻,或者它们是相邻的
无向图 :无向图中的一个边可以在任一方向上遍历
路径::通过边连接的顶点序列
周期:第一个和最后一个顶点相同的路径
入度::顶点的度数V是以V为端点的边数
出度: 顶点的出度v是以v为起点的边的数量
度:顶点的度数是其入度和出度的总和
图的ADT
数据成员 :
顶点 (vertex)
边缘 (edge)
操作 :
有多少顶点?
有多少个边缘?
添加一个新的顶点
添加一个新的边缘
获取所有邻居? (进出)
U,V连接吗?
反转所有边缘?
获取2跳邻居
图表示法:邻接矩阵

class Vertex: def __init__(self, node): self.id = node # Mark all nodes unvisited self.visited = False def addNeighbor(self, neighbor, G): G.addEdge(self.id, neighbor) def getConnections(self, G): return G.adjMatrix[self.id] def getVertexID(self): return self.id def setVertexID(self, id): self.id = id def setVisited(self): self.visited = True def __str__(self): return str(self.id) class Graph: def __init__(self, numVertices=10, directed=False): self.adjMatrix = [[None] * numVertices for _ in range(numVertices)] self.numVertices = numVertices self.vertices = [] self.directed = directed for i in range(0, numVertices): newVertex = Vertex(i) self.vertices.append(newVertex) def addVertex(self, vtx, id): #增加点,这个function没有扩展功能 if 0 <= vtx < self.numVertices: self.vertices[vtx].setVertexID(id) def getVertex(self, n): for vertxin in range(0, self.numVertices): if n == self.vertices[vertxin].getVertexID(): return vertxin return None def addEdge(self, frm, to, cost=0): #返回全部连线/航线 #print("from",frm, self.getVertex(frm)) #print("to",to, self.getVertex(to)) if self.getVertex(frm) is not None and self.getVertex(to) is not None: self.adjMatrix[self.getVertex(frm)][self.getVertex(to)] = cost if not self.directed: # For directed graph do not add this self.adjMatrix[self.getVertex(to)][self.getVertex(frm)] = cost def getVertices(self): vertices = [] for vertxin in range(0, self.numVertices): vertices.append(self.vertices[vertxin].getVertexID()) return vertices def printMatrix(self): for u in range(0, self.numVertices): row = [] for v in range(0, self.numVertices): row.append(str(self.adjMatrix[u][v]) if self.adjMatrix[u][v] is not None else '/') print(row) def getEdges(self): edges = [] for v in range(0, self.numVertices): for u in range(0, self.numVertices): if self.adjMatrix[u][v] is not None: vid = self.vertices[v].getVertexID() wid = self.vertices[u].getVertexID() edges.append((vid, wid, self.adjMatrix[u][v])) return edges def getNeighbors(self, n): neighbors = [] for vertxin in range(0, self.numVertices): if n == self.vertices[vertxin].getVertexID(): for neighbor in range(0, self.numVertices): if (self.adjMatrix[vertxin][neighbor] is not None): neighbors.append(self.vertices[neighbor].getVertexID()) return neighbors def isConnected(self, u, v): uidx = self.getVertex(u) vidx = self.getVertex(v) return self.adjMatrix[uidx][vidx] is not None def get2Hops(self, u): #转一次机可以到达哪里 neighbors = self.getNeighbors(u) print(neighbors) hopset = set() for v in neighbors: hops = self.getNeighbors(v) hopset |= set(hops) return list(hopset)
图表示法:邻接表
用邻接矩阵来表示,每一行表示一个节点与其他所有节点是否相连,但对于邻接表来说,一行只代表和他相连的节点:
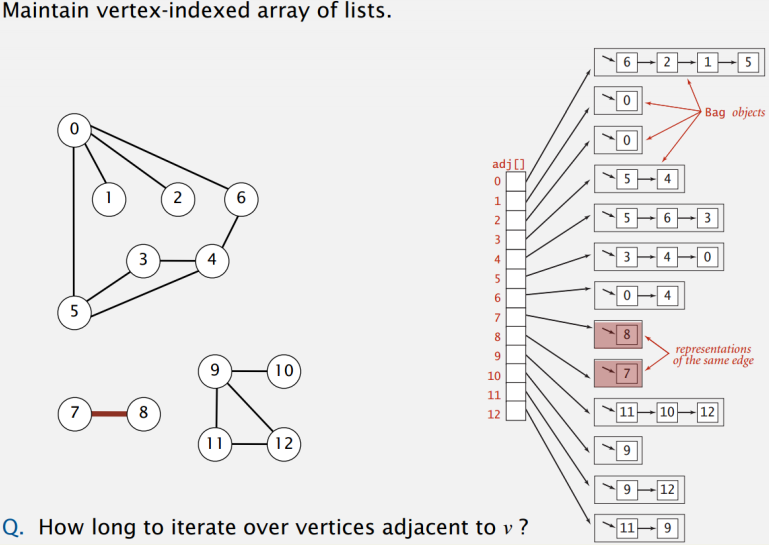
可见邻接表在空间上是更省资源的。
邻接表适合表示稀疏图,邻接矩阵适合表示稠密图。
import sys class Vertex: def __init__(self, node): self.id = node self.adjacent = {} #为所有节点设置距离无穷大 self.distance = sys.maxsize # 标记未访问的所有节点 self.visited = False # Predecessor self.previous = None def addNeighbor(self, neighbor, weight=0): self.adjacent[neighbor] = weight # returns a list def getConnections(self): # neighbor keys return self.adjacent.keys() def getVertexID(self): return self.id def getWeight(self, neighbor): return self.adjacent[neighbor] def setDistance(self, dist): self.distance = dist def getDistance(self): return self.distance def setPrevious(self, prev): self.previous = prev def setVisited(self): self.visited = True def __str__(self): return str(self.id) + ' adjacent: ' + str([x.id for x in self.adjacent]) def __lt__(self, other): return self.distance < other.distance and self.id < other.id class Graph: def __init__(self, directed=False): # key is string, vertex id # value is Vertex self.vertDictionary = {} self.numVertices = 0 self.directed = directed def __iter__(self): return iter(self.vertDictionary.values()) def isDirected(self): return self.directed def vectexCount(self): return self.numVertices def addVertex(self, node): self.numVertices = self.numVertices + 1 newVertex = Vertex(node) self.vertDictionary[node] = newVertex return newVertex def getVertex(self, n): if n in self.vertDictionary: return self.vertDictionary[n] else: return None def addEdge(self, frm, to, cost=0): if frm not in self.vertDictionary: self.addVertex(frm) if to not in self.vertDictionary: self.addVertex(to) self.vertDictionary[frm].addNeighbor(self.vertDictionary[to], cost) if not self.directed: # For directed graph do not add this self.vertDictionary[to].addNeighbor(self.vertDictionary[frm], cost) def getVertices(self): return self.vertDictionary.keys() def setPrevious(self, current): self.previous = current def getPrevious(self, current): return self.previous def getEdges(self): edges = [] for key, currentVert in self.vertDictionary.items(): for nbr in currentVert.getConnections(): currentVertID = currentVert.getVertexID() nbrID = nbr.getVertexID() edges.append((currentVertID, nbrID, currentVert.getWeight(nbr))) # tuple return edges def getNeighbors(self, v): vertex = self.vertDictionary[v] return vertex.getConnections()
学习资料参考:图论算法初步、python算法图论