本篇我以队列的数据类型和操作方法两个方面总结学习笔记
队列(Queue)
- 一种先进先出(FIFO)的线性数据结构,插入操作在队尾(tail)进行,删除操作在队首(head)进行。
- 列可以通过(循环)数组或链表轻松实现
一、数据类型
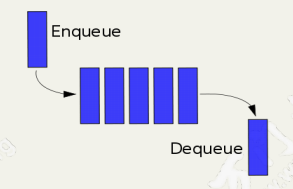
Queue()创建队列enqueue(item)向队尾插入项dequeue()返回队首的项,并从队列中删除该项empty()判断队列是否为空size()返回队列中项的个数
操作示意图
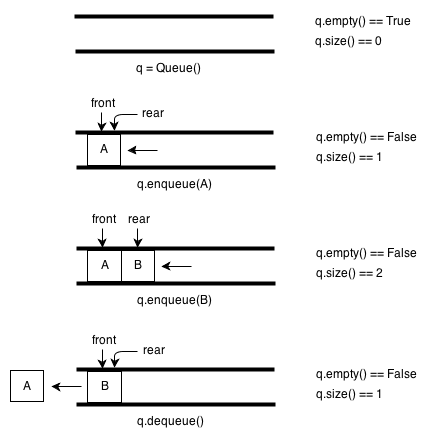
注:front即head,rear即tail
二、代码实现
''' 使用Python的内建类型list列表实现很方便 ''' class Queue(): def __init__(self): self.items = [] #增于尾后tail def enqueue(self, item): self.items.append(item) #删于头首head def dequeue(self): return self.items.pop(0) def empty(self): return self.size() == 0 def size(self): return len(self.items)
''' 动态数组实现队列并不用内置方法 ''' class ArrayQueue: DEFAULT_CAPACITY = 10 def __init__(self): self._data = [None] * ArrayQueue.DEFAULT_CAPACITY self._size = 0 self._front = 0 def __len__(self): return self._size def is_empty(self): return self._size == 0 #O(1) def first(self): if self.is_empty( ): raise ValueError( 'Queue is empty' ) return self._data[self._front] #O(1) def dequeue(self): if self.is_empty( ): raise ValueError( 'Queue is empty' ) answer = self._data[self._front] self._data[self._front] = None self._front = (self._front + 1) % len(self._data) self._size -= 1 return answer #O(1) def enqueue(self, e): if self._size == len(self._data): self._resize(2 * len(self._data)) #如果满了开拓两倍空间 pos = (self._front + self._size) % len(self._data) self._data[pos] = e self._size += 1 def resize(self, cap): old = self._data self._data = [None] * cap walk = self._front for k in range(self._size): self._data[k] = old[walk] walk = (1 + walk) % len(old) self._front = 0 def printqueue(self): for i in range(self._size): pos = (self._front + self._size - 1 - i) % len(self._data) #print(str(i), ": ", str(pos)) print(self._data[pos], end = " ") print()
''' 链表 模块方法来自链表笔记代码 ''' from LinkedList import LinkedList from LinkedList import Node class LinkedQueue(object): def __init__(self): self.head = None self.tail = None self.count = 0 #O(1) def enqueue(self, value): new_node = Node(value) if self.tail is not None: self.tail.next = new_node else: self.head = new_node self.tail = new_node self.count += 1 #O(1) def dequeue(self): if not self.is_empty(): # print head to next node tmp = self.head self.head = self.head.next print("dequeue sucess") self.count -= 1 return tmp else: raise ValueError("Empty QUEUE") def is_empty(self): if self.head is None and self.tail is None: return True else: return False def peek(self): return self.head.data def __len__(self): return self.count def is_empty(self): return self.count == 0 def print(self): node = self.head while node: print(node.value, end = " ") node = node.next print('')