Problem
(frac{3y^2+1}{y^3+y}cdot frac{ ext{d}y}{ ext{d}x}=2x,~y(0)=1),求 (y=4) 时 (x) 的值。
Solution
1
[int frac{3y^2+1}{y^3+y}~ ext{d}y=x^2+C
]
2
[egin{align}
int frac{3y^2+1}{y^3+y}~ ext{d}y & = int frac{3y^2+3-2}{y(y^2+1)}~ ext{d}y
onumber\
& = int frac{3}{y}~ ext{d}y-int frac{2}{y(y^2+1)}~ ext{d}y
onumber\
& = 3ln |y|-int frac{2}{y(y^2+1)}~ ext{d}y
onumber
end{align}
]
3
简化 (int frac{2}{y(y^2+1)}~ ext{d}y)。
[
onumber
egin{align}
frac{A}{y}+frac{By+C}{y^2+1}=frac{2}{y(y^2+1)}
onumber\
Ay^2+A+By^2+Cy=2
onumber
end{align}
]
得 (A+B=0,~C=0,~A=2),即 (A=2,~B=-2,~C=0)。
即
[egin{align}
int frac{2}{y(y^2+1)}~ ext{d}y&=intfrac{2}{y}~ ext{d}y-intfrac{2y}{y^2+1}~ ext{d}y
onumber\
&=2ln |y|-intfrac{2y}{y^2+1}~ ext{d}y
onumber
end{align}
]
3.1
简化 (intfrac{2y}{y^2+1}~ ext{d}y)。
令 (u=y^2+1),则 ( ext{d}u=2y),即 (intfrac{2y}{y^2+1}~ ext{d}y=int frac{1}{u}~ ext{d}u=ln u=ln (y^2+1))
4
综合以上各式,得 (3ln |y|-2ln |y|+ln(y^2+1)=x^2+C)。
代入 (x=0,~y=1) 得 (C=ln 2)。
代入 (y=4) 得 (x=sqrt{ln 4+ln 17-ln 2}=sqrt{ln frac{4cdot 17}{2}}=sqrt{ln{34}})
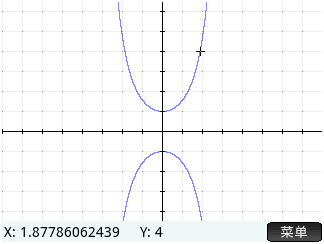
Graph