99. 恢复二叉搜索树

给你二叉搜索树的根节点 root ，该树中的两个节点被错误地交换。请在不改变其结构的情况下，恢复这棵树。

进阶：使用 O(n) 空间复杂度的解法很容易实现。你能想出一个只使用常数空间的解决方案吗？

示例 1：

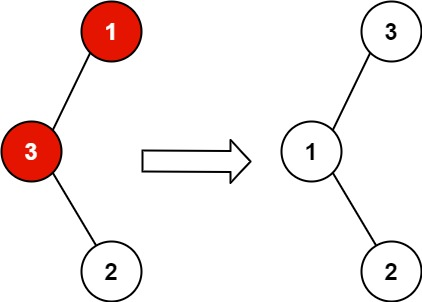
输入：root = [1,3,null,null,2]
输出：[3,1,null,null,2]
解释：3 不能是 1 左孩子，因为 3 > 1 。交换 1 和 3 使二叉搜索树有效。

示例 2：

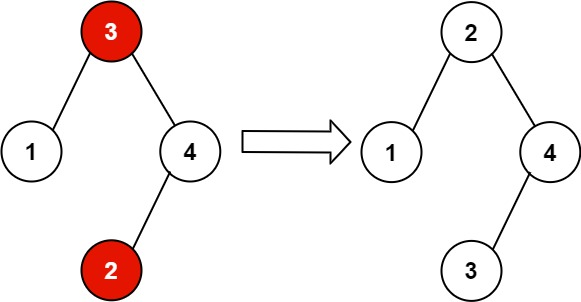
输入：root = [3,1,4,null,null,2]
输出：[2,1,4,null,null,3]
解释：2 不能在 3 的右子树中，因为 2 < 3 。交换 2 和 3 使二叉搜索树有效。

 

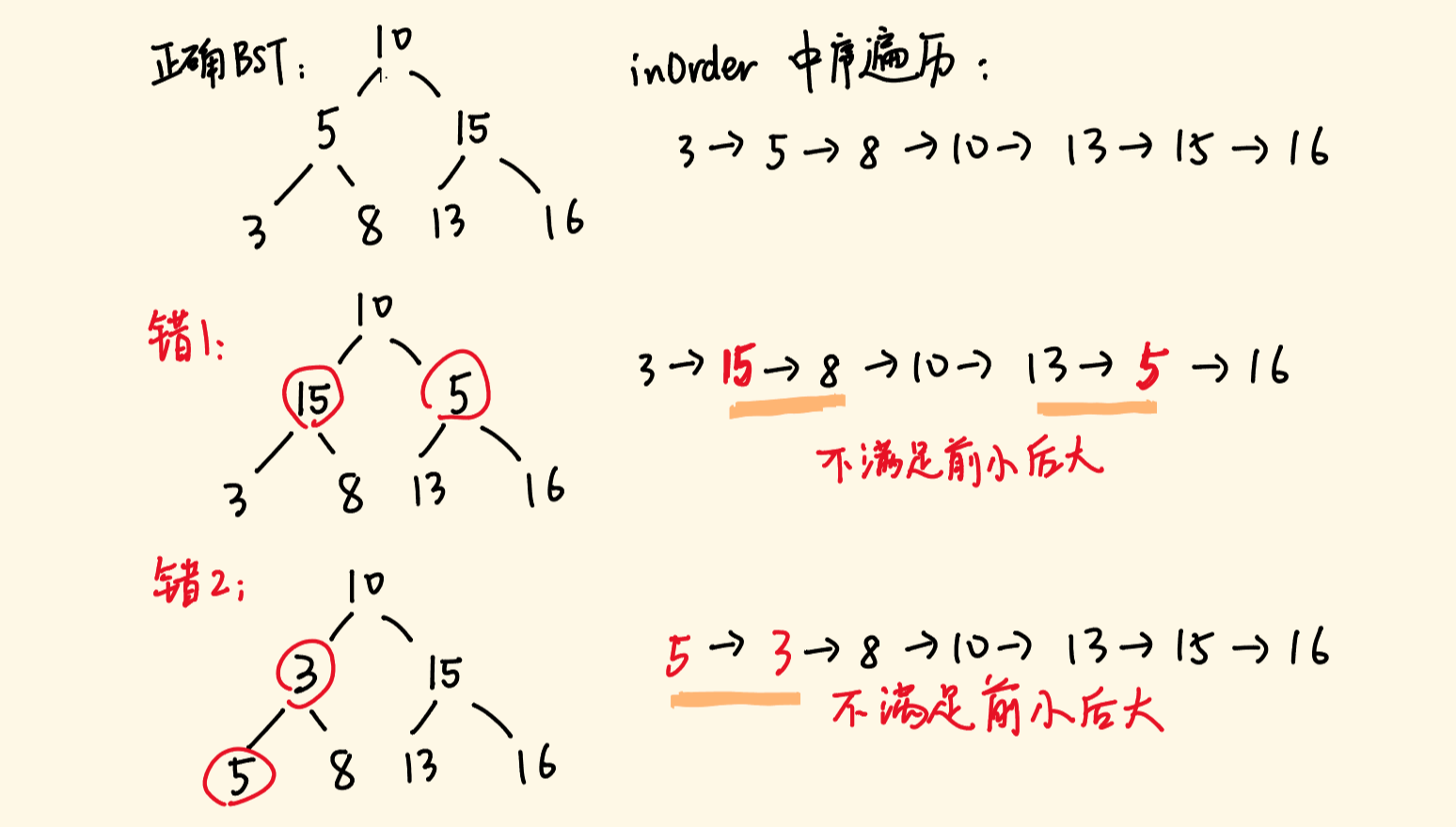
class Solution {
    //第一个前置节点，排序二叉树，这里第一个点直接默认最小值
    TreeNode prev=new TreeNode(Integer.MIN_VALUE);
    TreeNode err1=null,err2=null;
    public void recoverTree(TreeNode root) {
      //根据题意知，是两个节点的位置错误了，所以有两种情况
        //1.相邻的两个节点顺序错了，2.不相邻的，不相邻的第一处肯定是前大后小，第二处是前小后大
        helper(root);
        int temp=err1.val;
        err1.val=err2.val;
        err2.val=temp;
    }
    //辅助函数
   //中序遍历对于排序二叉树就是有顺序的
    void helper(TreeNode root){
        if(root==null){
            return;
        }
        helper(root.left);
        //中序遍历代码
        //不满足前小后大,就说明这是一个错误点
        //根据楼主的图可以看出分为两种情况
        //其中第二幅图看出，不相邻的情况下第一处肯定是前大后小，第二处是前小后大，
        // 所以在第一个错误点是pre，第二个错误点是root,
        // 这同时也满足了如果这两个错误点相邻的（第一幅图）情况
        //这也就是为什么要用两个if的原因，而不是把他们写到一个if里
        if(prev.val>root.val&&err1==null) {
            err1=prev;
        }
        if(prev.val>root.val&&err1!=null) {
            err2=root;
        }
        //当前点用完，就更新前置点
        prev=root;
        helper(root.right);
    }
}

package code;

import java.util.Stack;
/*
 * 99. Recover Binary Search Tree
 * 题意：二叉搜索树中两个节点错位了，恢复二叉搜索树，用O(1)空间
 * 难度：Hard
 * 分类：Tree, Depth-first Search
 * 思路：只要记录错乱的节点就可以了，最后交换两个节点的值
 *      先序遍历  在print那个地方加上逻辑代码
 * Tips：
 */
public class lc99 {
    public class TreeNode {
        int val;
        TreeNode left;
        TreeNode right;
        TreeNode(int x) {
            val = x;
        }
    }

    TreeNode tn1 = null;
    TreeNode tn2 = null;
    public void recoverTree(TreeNode root) {
        inorder(root);
        int temp = tn1.val;
        tn1.val = tn2.val;
        tn2.val = temp;
    }

    public void inorder(TreeNode root){
        TreeNode pre = null;
        Stack<TreeNode> st = new Stack();
        while(root!=null || !st.isEmpty()){
            while(root!=null){
                st.add(root);
                root = root.left;
            }
            root = st.pop();
            if(pre!=null && pre.val>root.val && tn1==null)
                tn1 = pre;
            if(pre!=null && pre.val>root.val && tn1!=null)   //可能被执行多次  eg  3 2 1  tn2 先被赋值2 后被赋值1
                tn2 = root;
            pre = root;
            root = root.right;
        }
    }
}