DS博客作业03--树

这个作业属于哪个班级	数据结构--网络2011/2012
这个作业的地址	DS博客作业03--树
这个作业的目标	学习树结构设计及运算操作
姓名	吴俊豪

0. PTA得分截图

1. 本周学习总结

1.1 二叉树结构

1.1.1 二叉树的2种存储结构

顺序存储:

优点: 存储地址相邻,存储空间利用率高;
缺点: 对树中元素数据修改操作繁琐.

链式存储

优点: 修改元素数据时很方便，操作简单;
缺点: 存储空间利用率低.

1.1.2 二叉树的构造

顺序构造二叉树:

BinTree CreatBinTree(string str, int i)//顺序创建树
{
    int len;
    len = str.size();
    BinTree bt;
    bt = new TNode;
    if (i > len-1 || i <= 0)
    {
        return NULL;
    }
    if (str[i] == '#')
    {
        return NULL;
    }
    bt->Data = str[i];
    bt->lchild = CreatBinTree(str, 2 * i);
    bt->rchild = CreatBinTree(str, 2 * i + 1);
    return bt;
}

先序构造二叉树:

BTree PreCreatTree(string str, int &i)//先序创建树
{
    int len;
    len = str.size();
    BTree bt;
    if (i > len - 1)
    {
        return NULL;
    }
    if (str[i] == '#')
    {
        return NULL;
    }
    bt = new BTNode;
    bt->data = str[i];
    bt->lchild = PreCreatTree(str, ++i);
    bt->rchild = PreCreatTree(str, ++i);
    return bt;
}

中序构造二叉树

BTree InCreatTree(string str, int &i)//中序创建树
{
    int len;
    len = str.size();
    BTree bt;
    if (i > len - 1)
    {
        return NULL;
    }
    if (str[i] == '#')
    {
        return NULL;
    }
    bt = new BTNode;
    bt->lchild = CreatTree(str, ++i);
    bt->data = str[i];
    bt->rchild = CreatTree(str, ++i);
    return bt;
}

后序构造二叉树

BTree CreatTree(string str, int &i)//后序创建树
{
    int len;
    len = str.size();
    BTree bt;
    if (i > len - 1)
    {
        return NULL;
    }
    if (str[i] == '#')
    {
        return NULL;
    }
    bt = new BTNode;
    bt->lchild = CreatTree(str, ++i);
    bt->rchild = CreatTree(str, ++i);
    bt->data = str[i];
    return bt;
}

1.1.3 二叉树的遍历

先序/中序/后序 遍历

先序遍历:根->左->右,rt

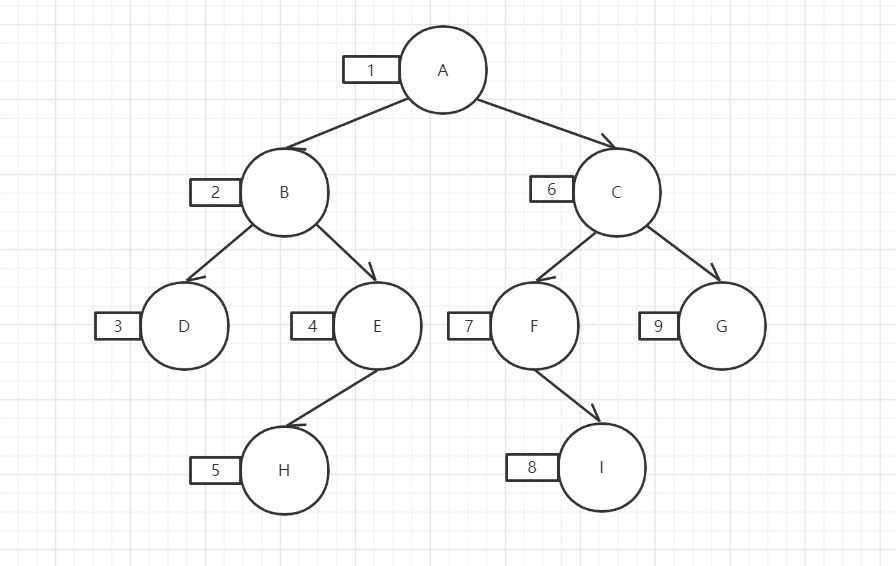
中序遍历:左->根->右,rt

后序遍历:左->右->根,rt

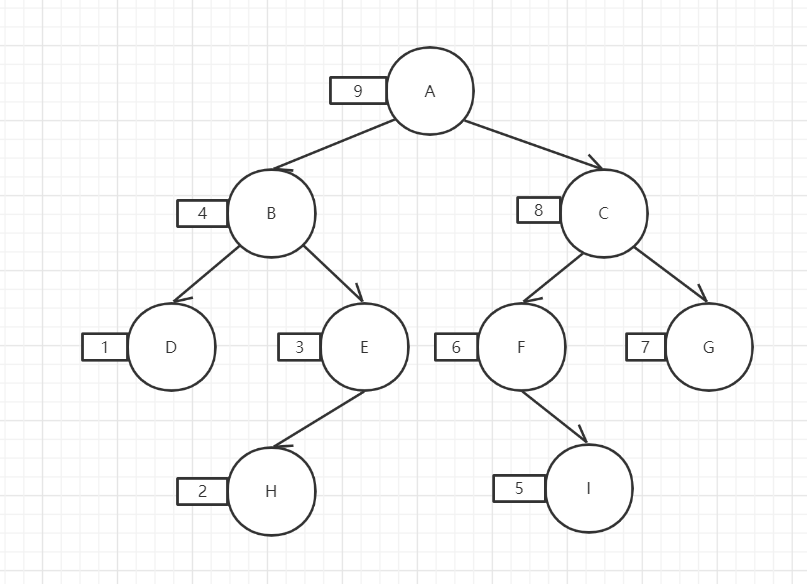
代码实现:

void OrderTree(BTree T)
{
    if (T == NULL)
    {
        return;
    }
    /*先序*/
    printf("%c ", T->data);
    OrderTree(T->lchild);
    OrderTree(T->rchild);

    /*中序*/
    OrderTree(T->lchild);
    printf("%c ", T->data);
    OrderTree(T->rchild);

    /*后序*/
    OrderTree(T->lchild);
    OrderTree(T->rchild);
    printf("%c ", T->data);
}

1.1.4 线索二叉树

使用线索二叉树是为了解决无法直接找到该结点在某种遍历序列中的前驱和后继结点的问题

设计线索二叉树

/* 二叉树的二叉线索存储结构定义*/
typedef enum{Link, Thread}PointerTag;    //Link = 0表示指向左右孩子指针；Thread = 1表示指向前驱或后继的线索
 
typedef struct BitNode
{
       char data;                                      //结点数据
       struct BitNode *lchild, *rchild;                //左右孩子指针
       PointerTag  ltag;                               //左右标志
       PointerTag  rtal;
}BitNode, *BiTree;

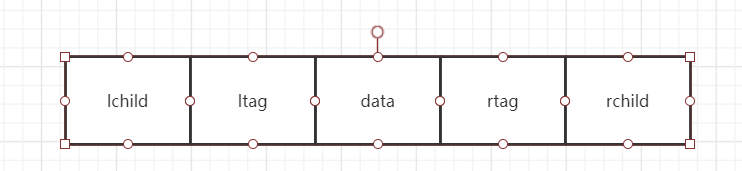
如果ptr->lchild为空，则存放指向中序遍历序列中该结点的前驱结点。这个结点称为ptr的中序前驱；
如果ptr->rchild为空，则存放指向中序遍历序列中该结点的后继结点。这个结点称为ptr的中序后继.

找前驱:

binThiTree* preTreeNode(binThiTree* q) {
	binThiTree* cur;
	cur = q;
	if (cur->LTag == true) {
		cur = cur->lchild;
		return cur;
	}
	else{
		cur = cur->lchild;//进入左子树
		while (cur->RTag == false) {
			cur = cur->rchild;
		}//找到左子树的最右边结点
		return cur;
	}
}

找后继

binThiTree* rearTreeNode(binThiTree* q) {
	binThiTree* cur = q;
	if (cur->RTag == true) {
		cur = cur->rchild;
		return cur;
	}
	else {
		//进入到*cur的右子树
		cur = cur->rchild;
		while (cur->LTag == false) {
			cur = cur->lchild;
		}
		return cur;
	}
}

1.1.5 二叉树的应用--表达式树

构造表达式树

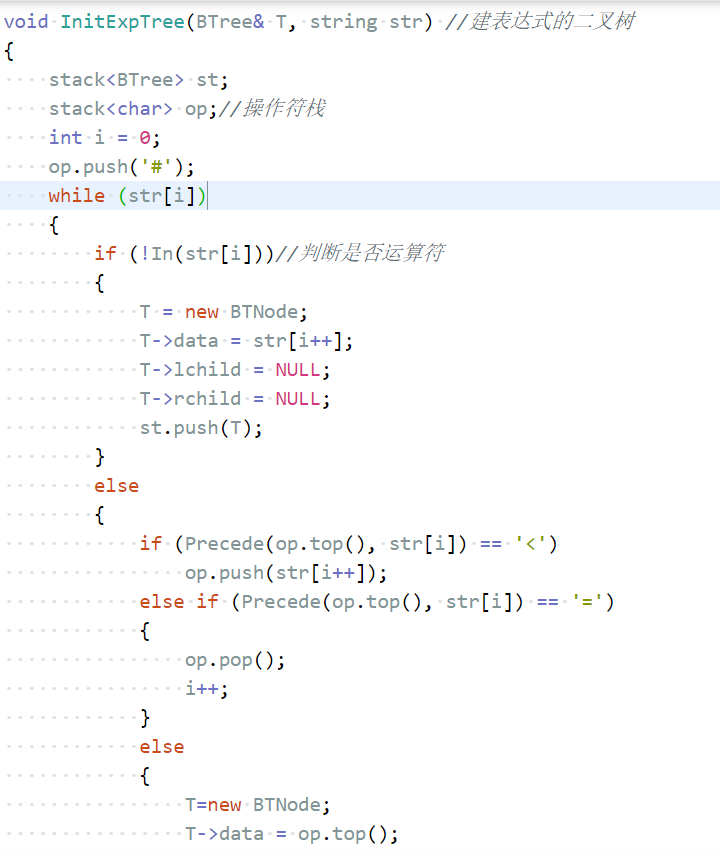
计算表达式树

1.2 多叉树结构

1.2.1 多叉树结构

由于多叉树其结点拥有多个子节点,进行定义和调用时的操作都会比较复杂,因此利用兄弟链的结构存储多叉树的子节点

1.2.2 多叉树遍历

先序遍历

1.3 哈夫曼树

1.3.1 哈夫曼树定义

哈夫曼树即WPL(带权路径长度)最小的二叉树,最小WPL唯一但哈夫曼树形状不一定唯一.

1.3.2 哈夫曼树的结构体

struct node{
	int val;	//记录权值 
	node *self = NULL;	//存自己的节点 
	node *left = NULL;	//左子节点 
	node *right = NULL;	//右子节点 
	bool operator < (const node &b)const{
		return val > b.val;
	}
};

1.3.2 哈夫曼树构建及哈夫曼编码

哈夫曼编码即是对一串数据长度的优化,将频率高的数据置于低深度的位置,频率低的数据作为高频数据的子节点,由此实现数据优化

1.4 并查集

当给出两个元素的一个无序对（a，b）时，需要快速“合并”a和b分别所在的集合，这期间需要反复“查找”某元素所在的集合，“并”，“查”，“集”由此而来。
在这种数据类型当中，n个不同的元素被分为若干组，每组是一个集合，这种集合叫做分离集合，称之为并查集。
由于我们的重点是在关注两个人是否连通，因此他们具体是如何连通的，内部结构是怎样的，甚至根节点是哪个，都不重要。
并查集一些简单操作

void Init(int father[], int n){
    for (int i = 0; i <= n; ++i)
    {
        father[i] = i;
    }
}

int findFather(int x){
    while(x != father[x]){
        x = father[x];
    }
    return x;
}

int findFather2(int x){
    if(x == father[x]) return x;
    else return findFather2(father[x]);
}

//合并
void Union(int a, int b){
    int faA = findFather(a);
    int faB = findFather(b);
    if(faA != faB){
        father[faA] = faB;
    }
}

2.PTA实验作业

输出二叉树每层节点
目录树

2.1 二叉树

2.1.1 解题思路及伪代码

输出二叉树每层节点:

void GetLevel(BTree T)
level, node用以判断层数和结点所在位置状态;
当前结点node=根结点T=队尾结点lastNode;
创建队列;
if (根结点为空)返回NULL;
将根结点入队;
while (队列不为空)
取队头为当前结点;
若有左孩子，将左孩子入队;
若有右孩子，将有孩子入队;
根据flag判断是从第几层开始，输出层数
if (到队尾)取队尾，输出结点数据,将标志改为1表示队头;
if(没到队尾)输出结点数据，改变或保持标志变量为0,
将该结点出队;
}

2.1.2 总结解题所用的知识点

队列操作+先序建树

2.2 目录树

2.2.1 解题思路及伪代码

struct node //结构体
{
    char* Name;
    Bool isMulu;//判断是否目录
    Node File;
    Node Mulu;
    Node Brother;
} Head;

解题思路:

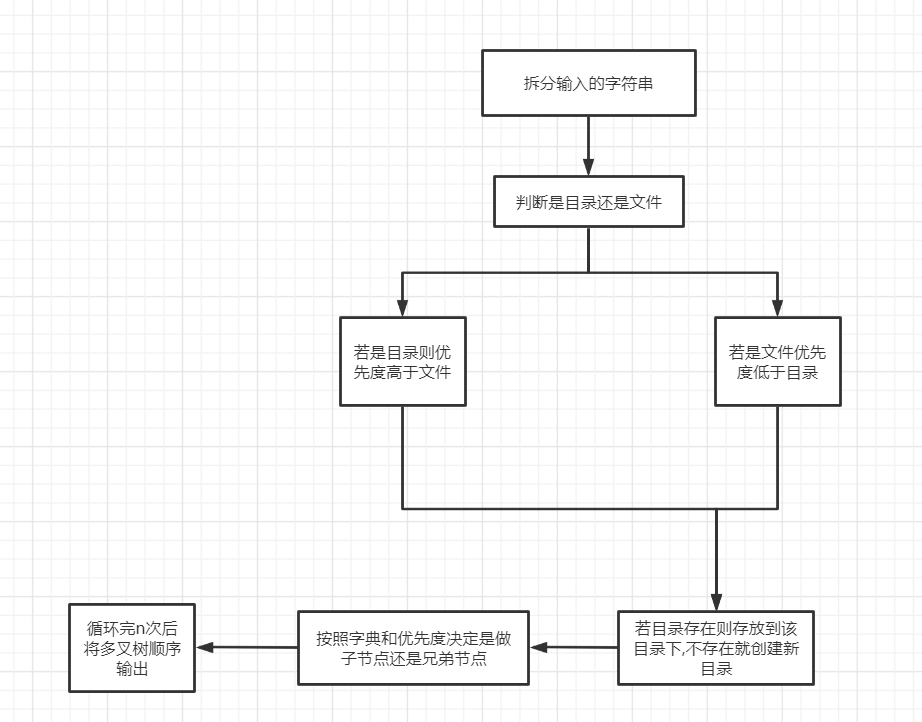
2.2.2 总结解题所用的知识点

创建多叉树+建立兄弟结点并插入+查找结点+先序遍历输出+后序遍历排序

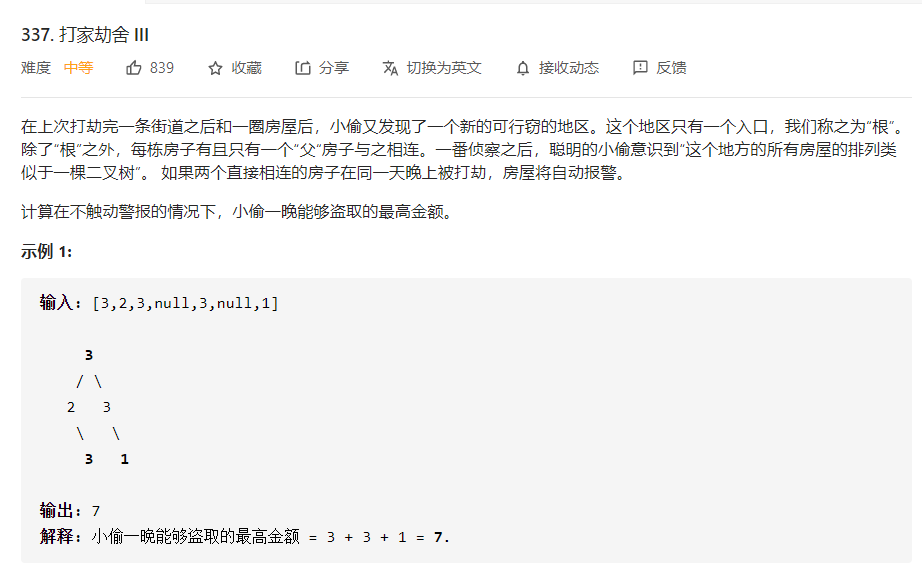
3.阅读代码

3.1 题目及解题代码

337.打家劫舍

class Solution {
public:
    unordered_map <TreeNode*, int> f, g;

    void dfs(TreeNode* node) {
        if (!node) {
            return;
        }
        dfs(node->left);
        dfs(node->right);
        f[node] = node->val + g[node->left] + g[node->right];
        g[node] = max(f[node->left], g[node->left]) + max(f[node->right], g[node->right]);
    }

    int rob(TreeNode* root) {
        dfs(root);
        return max(f[root], g[root]);
    }
};

3.2 该题的设计思路

简化一下这个问题：一棵二叉树，树上的每个点都有对应的权值，每个点有两种状态（选中和不选中），问在不能同时选中有父子关系的点的情况下，能选中的点的最大权值和是多少。
我们可以用 f(o)表示选择 o节点的情况下，o节点的子树上被选择的节点的最大权值和；g(o) 表示不选择 o 节点的情况下，o节点的子树上被选择的节点的最大权值和；l和 r代表o的左右孩子。

假设二叉树的节点个数为n,我们可以看出，以上的算法对二叉树做了一次后序遍历，时间复杂度是 O(n)；由于递归会使用到栈空间，空间代价是O(n)，哈希表的空间代价也是O(n)，故空间复杂度也是 O(n)。

当o被选中时o的左右孩子都不能被选中，故o被选中情况下子树上被选中点的最大权值和为l和r不被选中的最大权值和相加，即 f(o)=g(l)+g(r)。
当o不被选中时,o的左右孩子可以被选中，也可以不被选中。对于o的某个具体的孩子x,它对o的贡献是x被选中和不被选中情况下权值和的较大值。
至此，我们可以用哈希表来存f和g的函数值，用深度优先搜索的办法后序遍历这棵二叉树，我们就可以得到每一个节点的f和g。根节点的f和g的最大值就是我们要找的答案。

3.3 分析该题目解题优势及难点

优势:利用后序遍历完成对深度的搜索
难点:想不到用哈希数组来存放结点数据