本文概述:
一、计算机视觉(以下简称CV)概述
二、图像预处理
o 图像显示与存储原理(略)
o 图像增强的目标
o 图像处理方法
o 点运算:基于直方图的对比度增强
o 形态学处理(略)
o 空间域处理:卷积
o 卷积的应用(平滑、边缘检测、锐化等)
o 频率域处理:傅里叶变换、小波变换(略)
o 应用案例:
平滑、边缘检测、CLAHE等
一、CV研究内容概述:
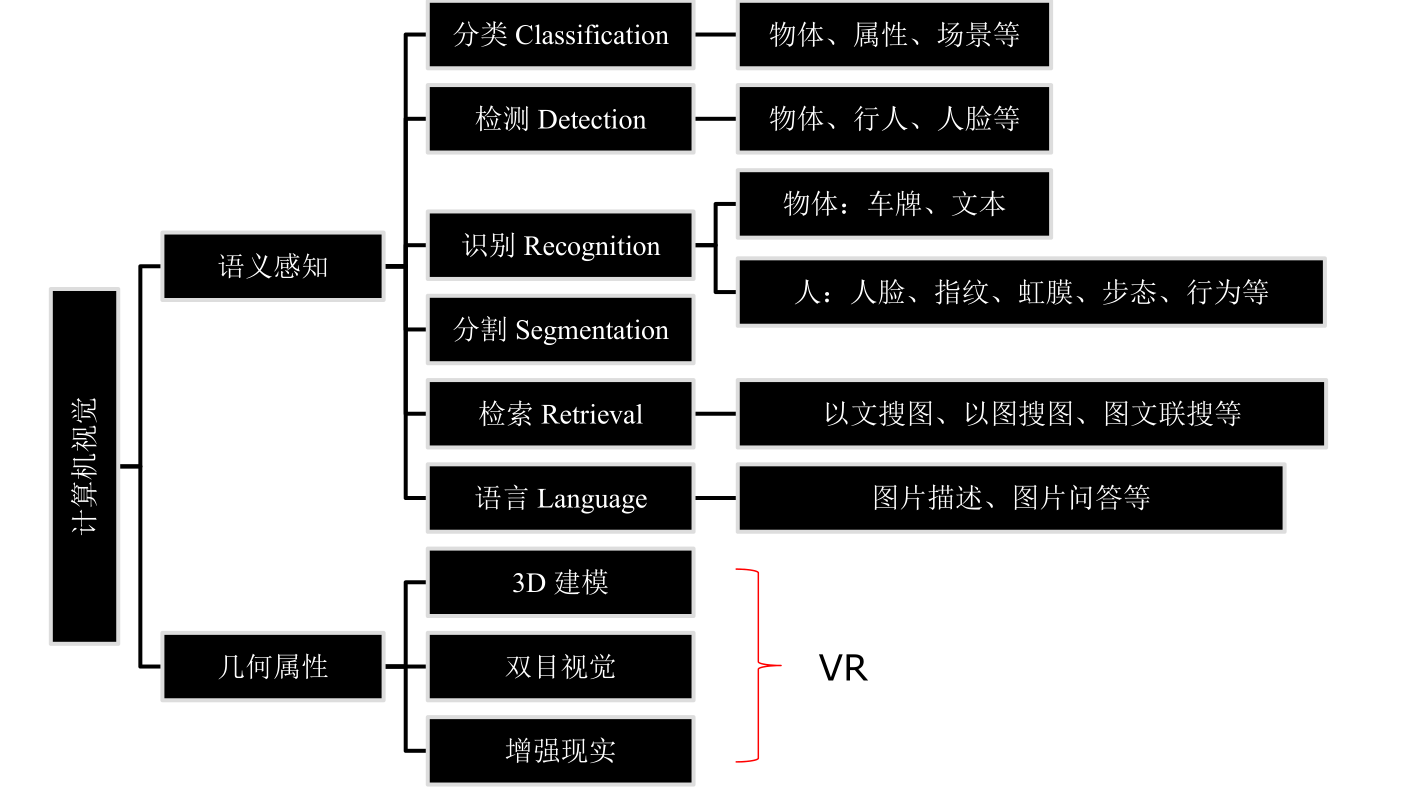

二、图像预处理
o 图像增强的目标

o 图像处理方法
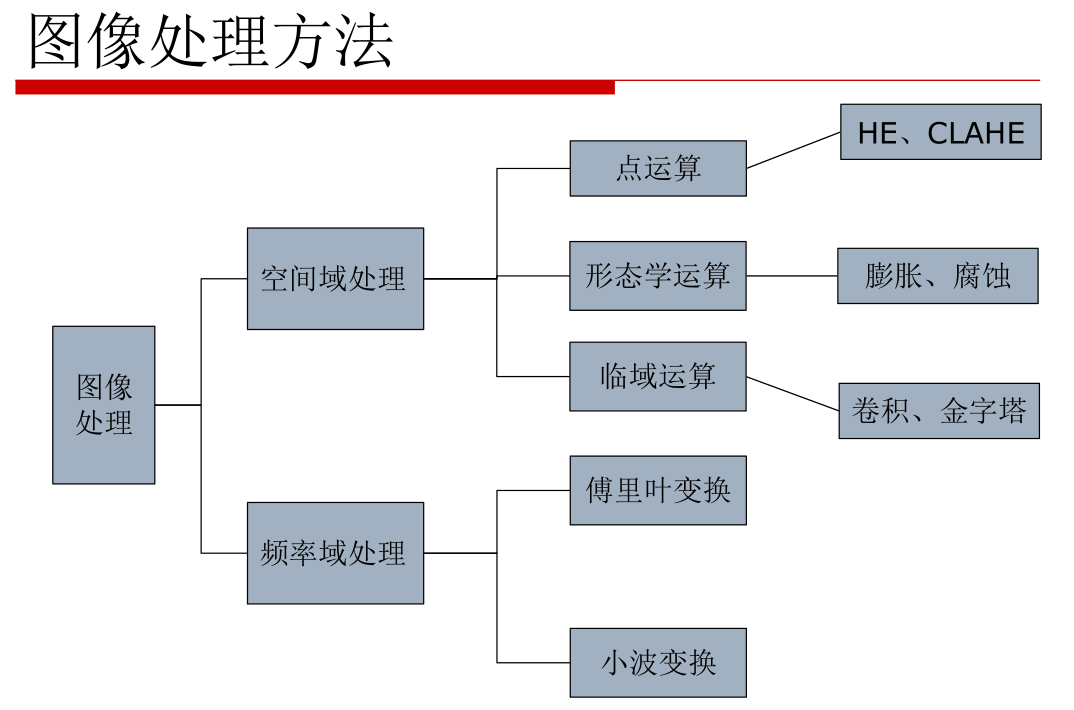
因为在CNN或者其他深度学习网络中,都需要对图片数据进行特征提取,才能进行学习。因此提取图片的特征非常重要,下面对特征提取进行简单介绍:
o 点运算:基于直方图的对比度增强
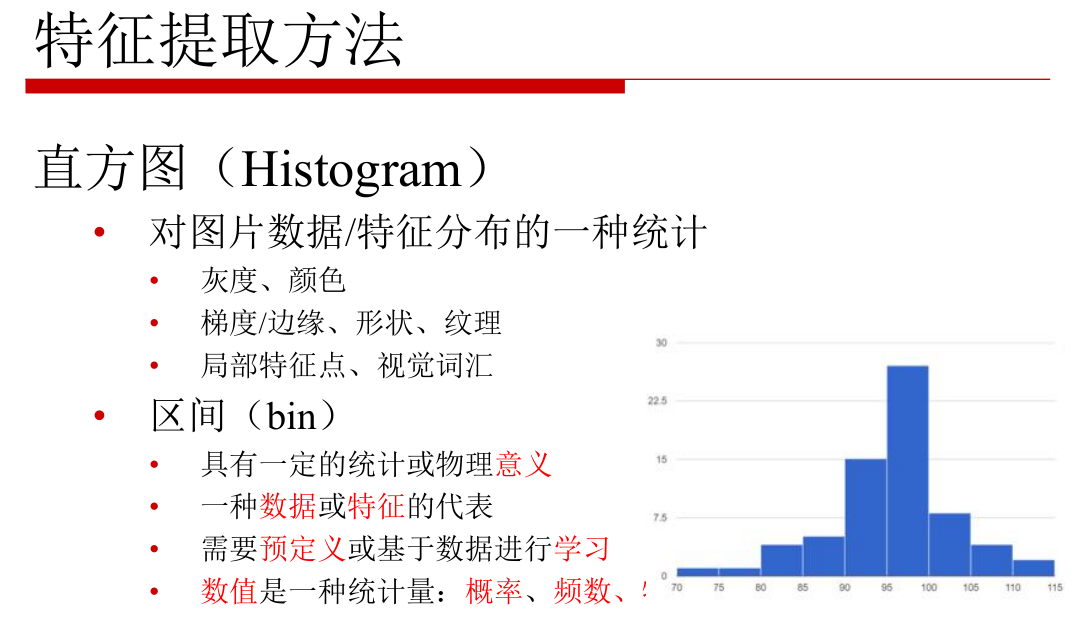
解释:
对图片数据/特征分布的一种统计,个人理解有点聚类的思想,就好比一件只有红色和蓝色的T恤,通过直方图的统计,最终可以得到T恤(这里只用颜色举例)的颜色分布的直方图。这就是提取其特征的一种方式。
这里的“灰度”:黑白图像中点的颜色深度,0~255,黑色是0,白色是255。灰度数字图像是每个像素只有一个采样颜色的图像。
每一个像素:有256个灰度等级(像素值在0~255之间),每个等级代表不同的亮度。
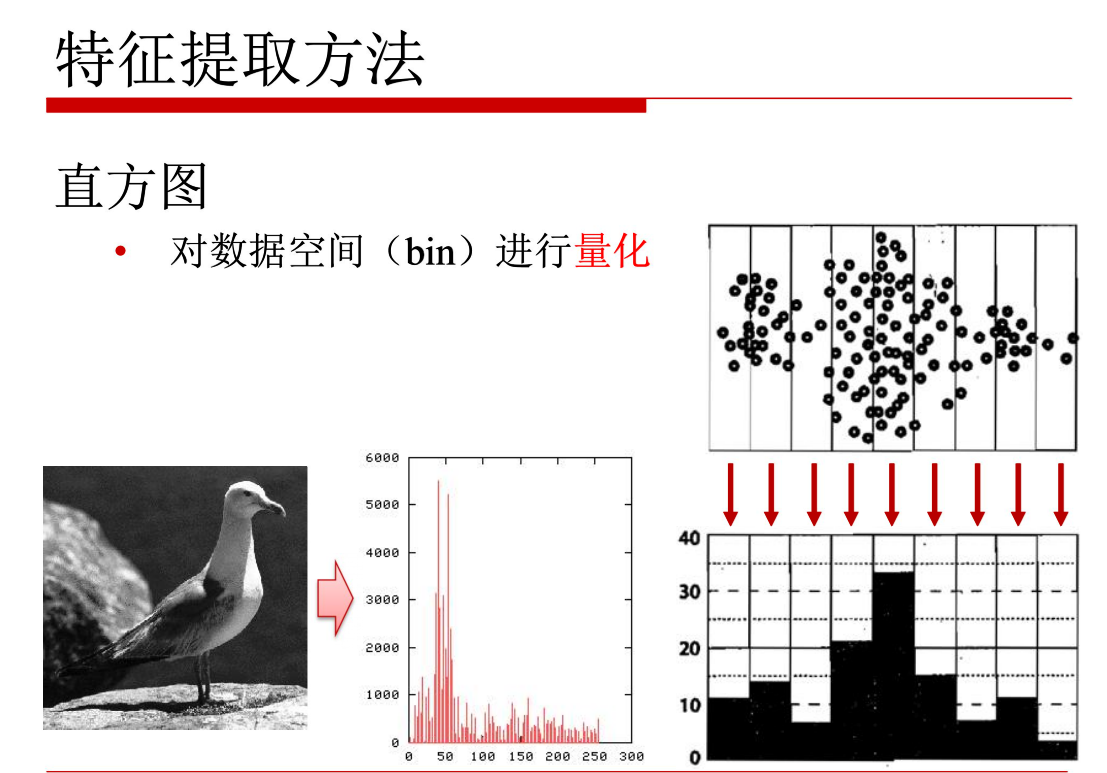
解释:
bin取的越大(最大255),则提前的特征分布越分散,每个像素统计出来,只对应一个区间(假设取255),
bin取的越小,比如取10,则这10个区间里可能包含多个不同数值的像素点。
为什么要进行直方图均衡化:
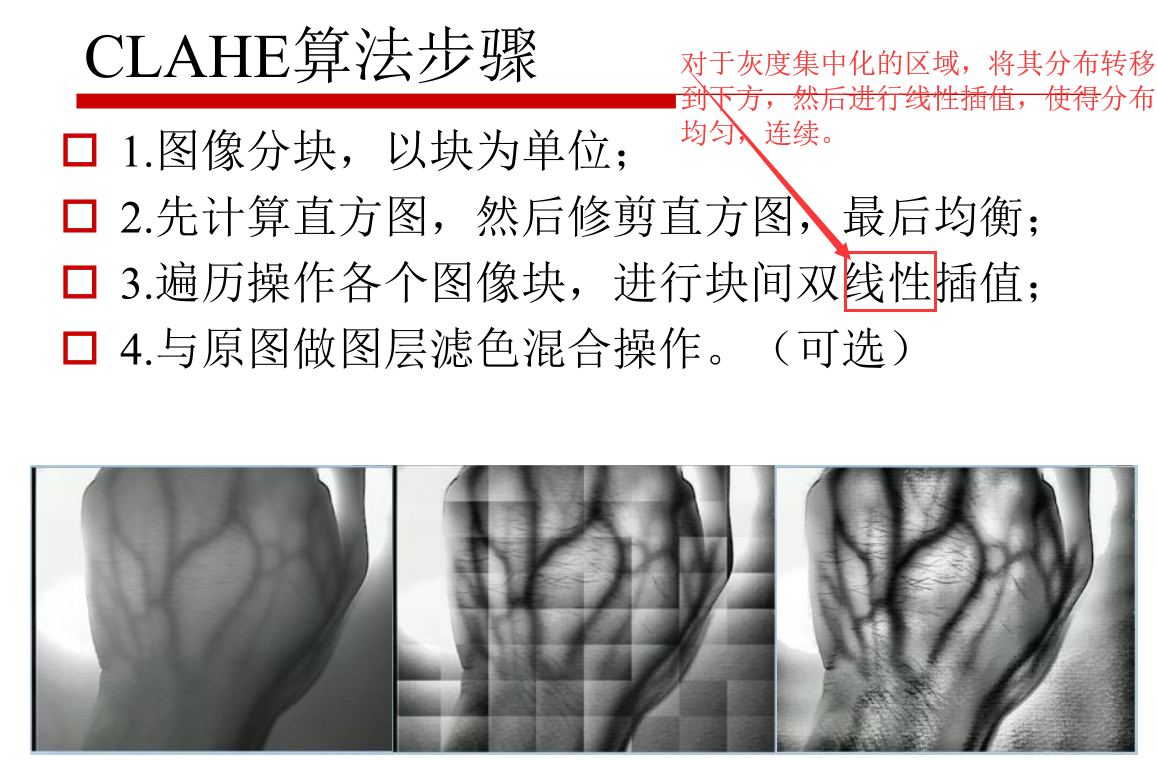
这是为了对图片进行调整,所拍的图,往往因为太亮或者太暗等因素造成了,局部的灰度集中化,因此需要一种手段,进行(非线性的)重新分配各个灰度单位中的像素点数量(具体方法,一般是最终使得一定灰度范围内像素点数量的值大致相同)

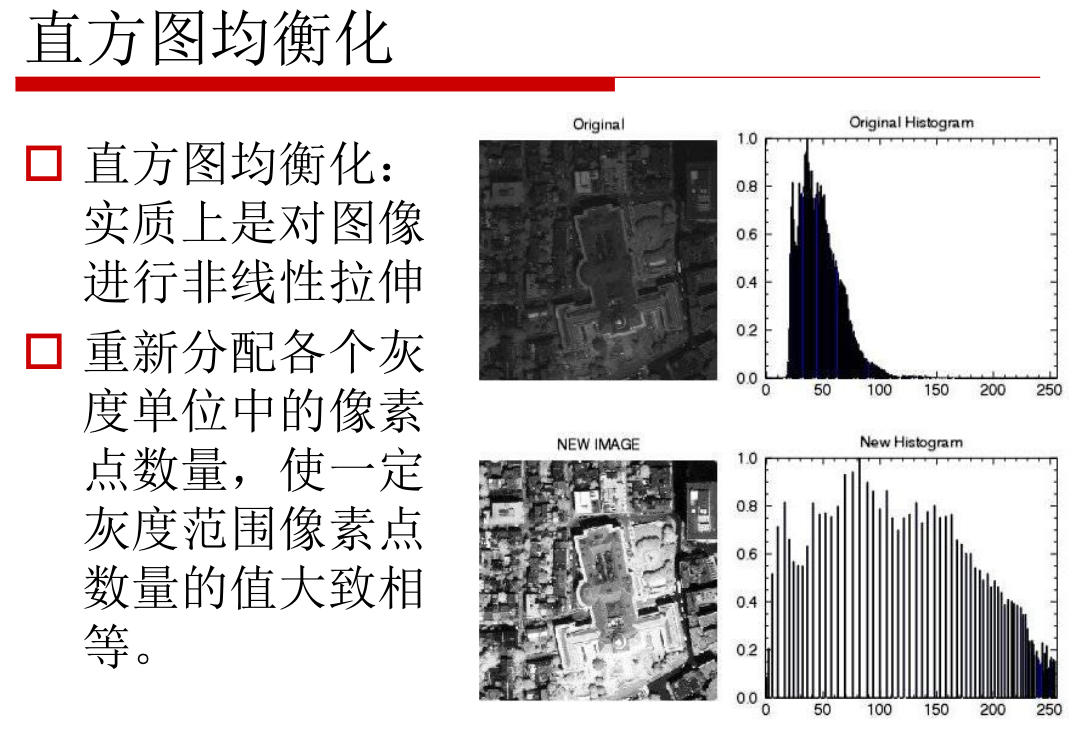

AHE的问题是:经过均衡化的图像往往不连续
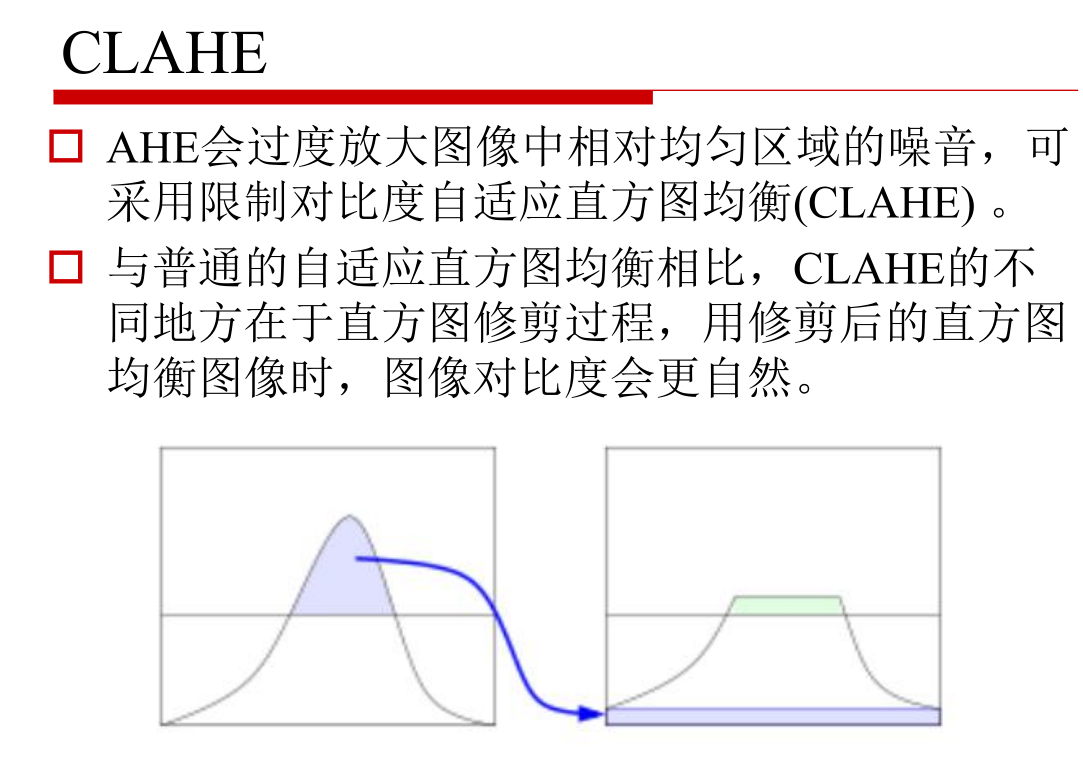
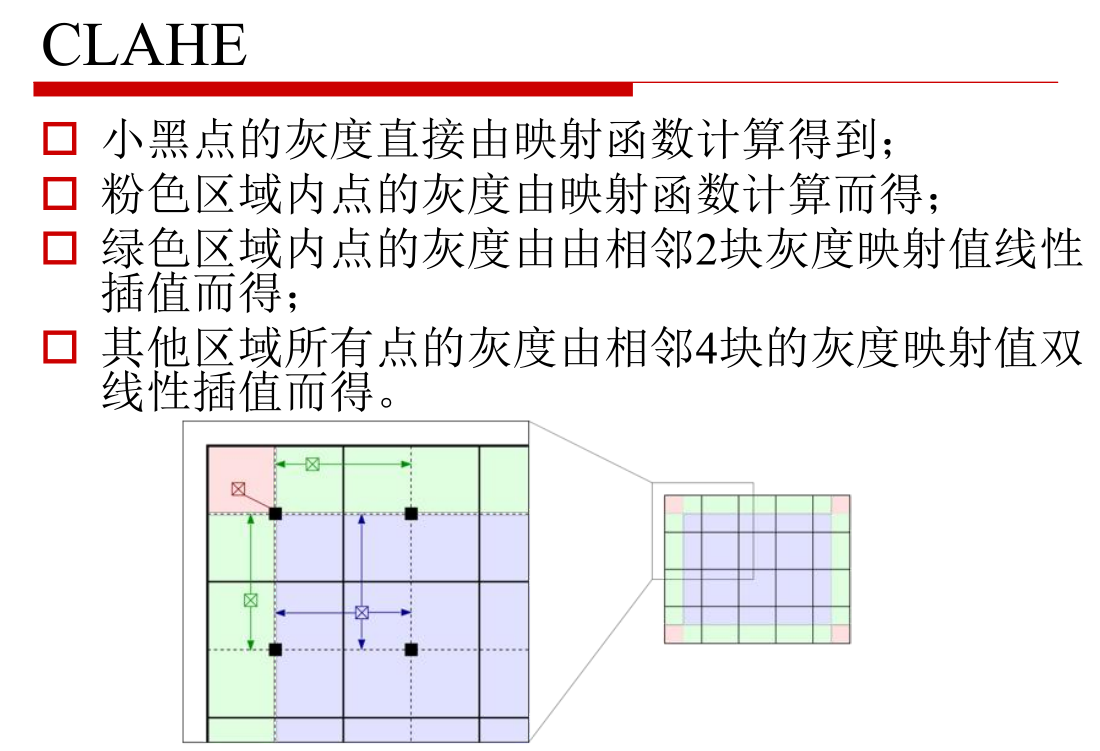
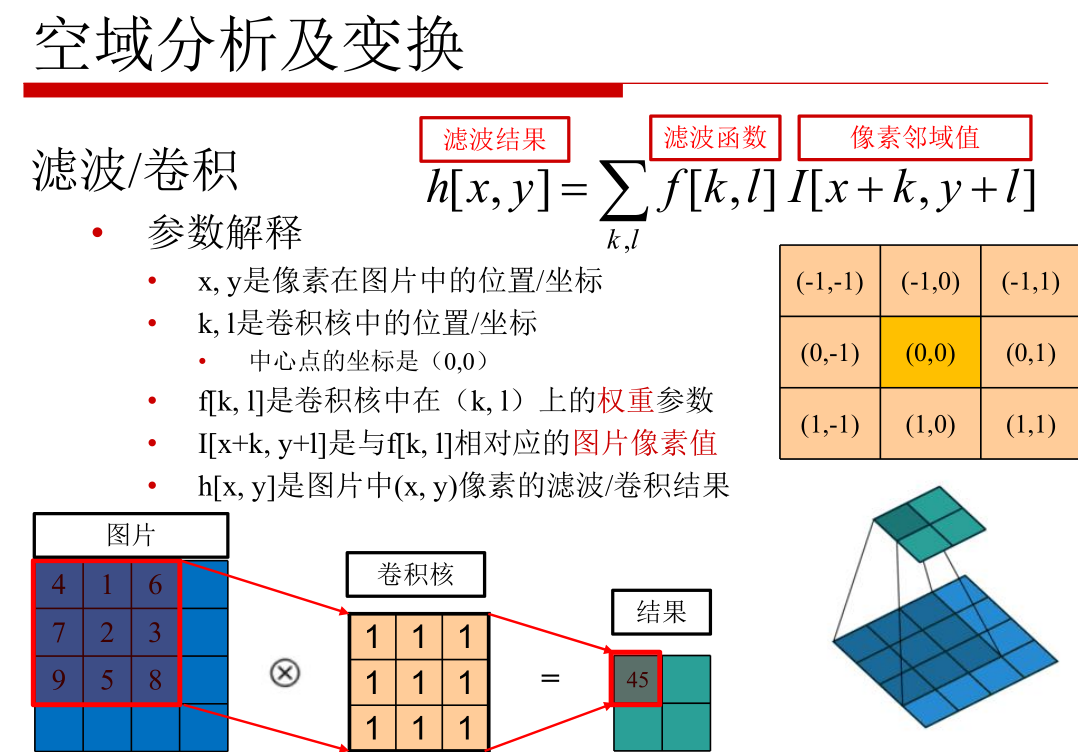
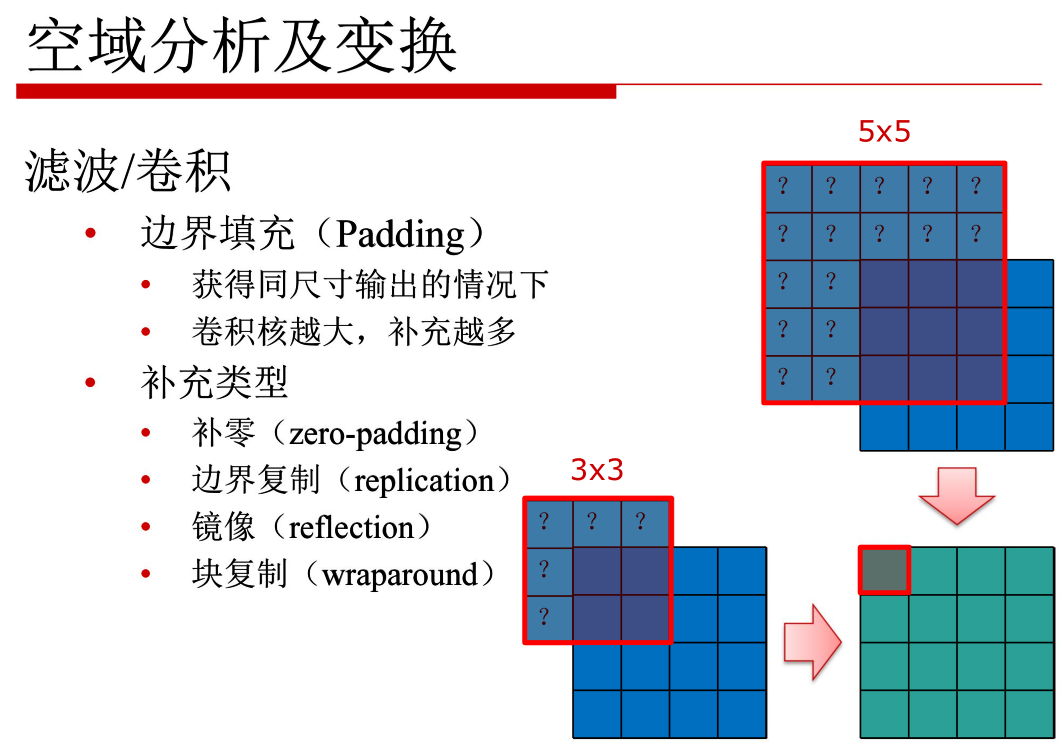
o 空间域处理:卷积


o 卷积的应用(平滑、边缘检测、锐化等)
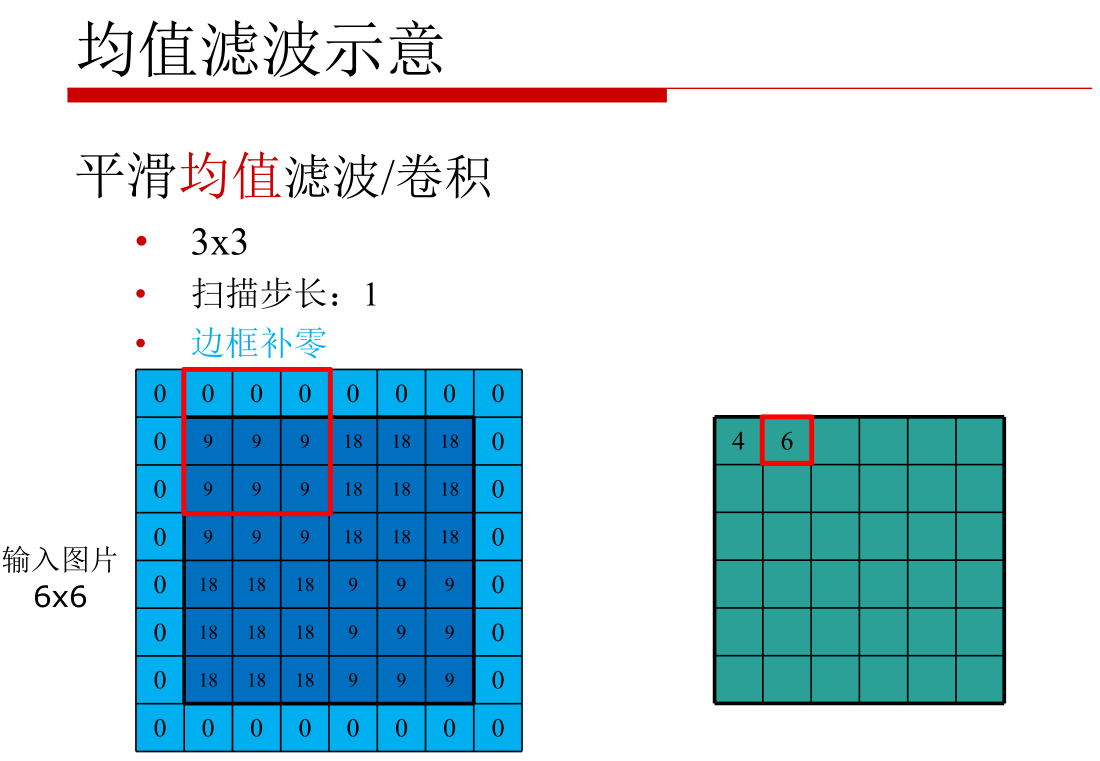
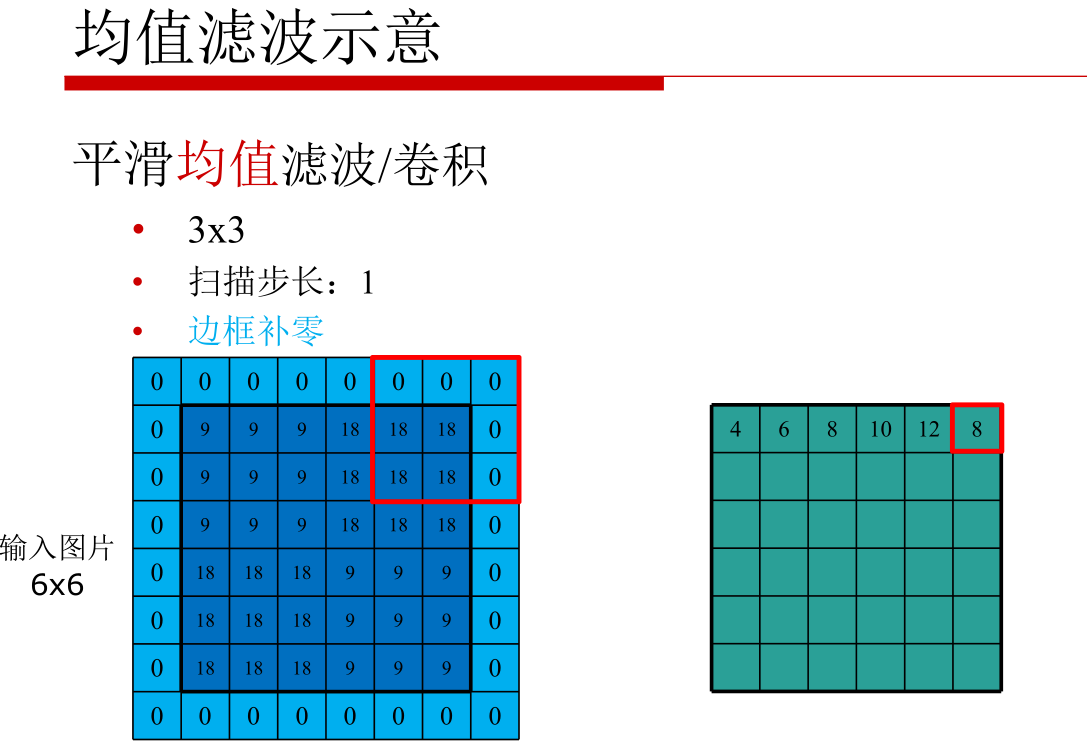
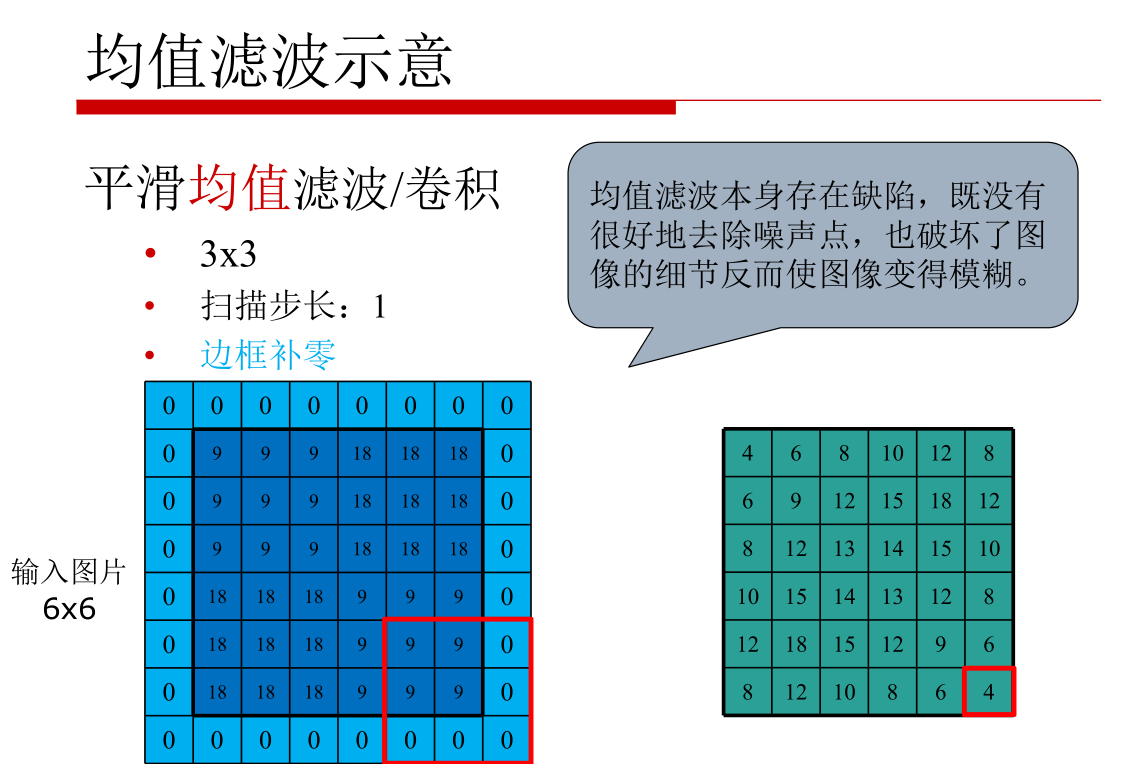

因为均值滤波有很大的缺陷,因此用的很少,下面介绍几种常见的滤波器
中值滤波:有效去除椒盐噪声
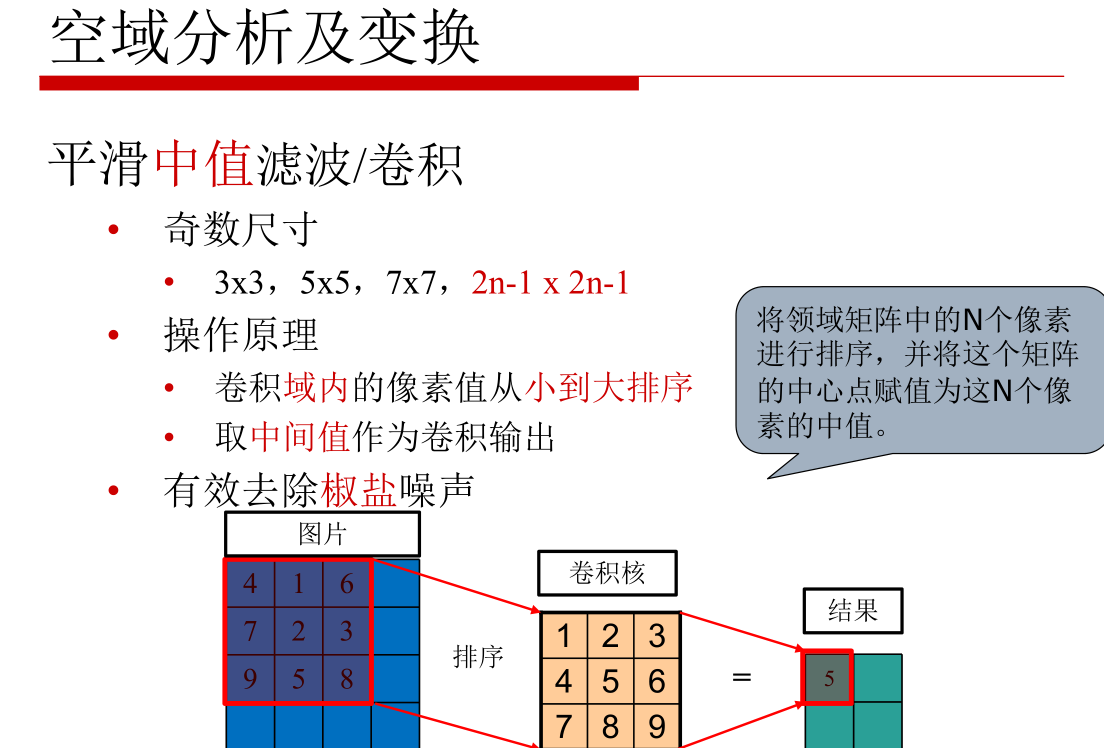

高斯滤波(重点):高斯滤波名字的由来,我的理解是,它的滤波器(卷积核)数值分布是高斯分布,它的应用必须结合后面要讲的高斯金字塔(捕捉不同尺寸的物体,尺寸缩小 + 高斯模糊)一起讲。
这里简单说明,高斯滤波其实是高斯模糊(blur),对于设定不同的标准差,高斯滤波将图片变换成不同清晰度。
标准差越大,大部分数值与均值差异较大,数据分布越离散,所用的高斯滤波器(卷积核)分布越尖锐(想象高斯分布尖尖的突出的曲线),所得的图片就会越模糊(但是所得的图像依旧是平缓的,是大致可以看出是什么物体的)。标准差越小则相反,高斯滤波器分布越平缓,所得图片不会那么模糊。
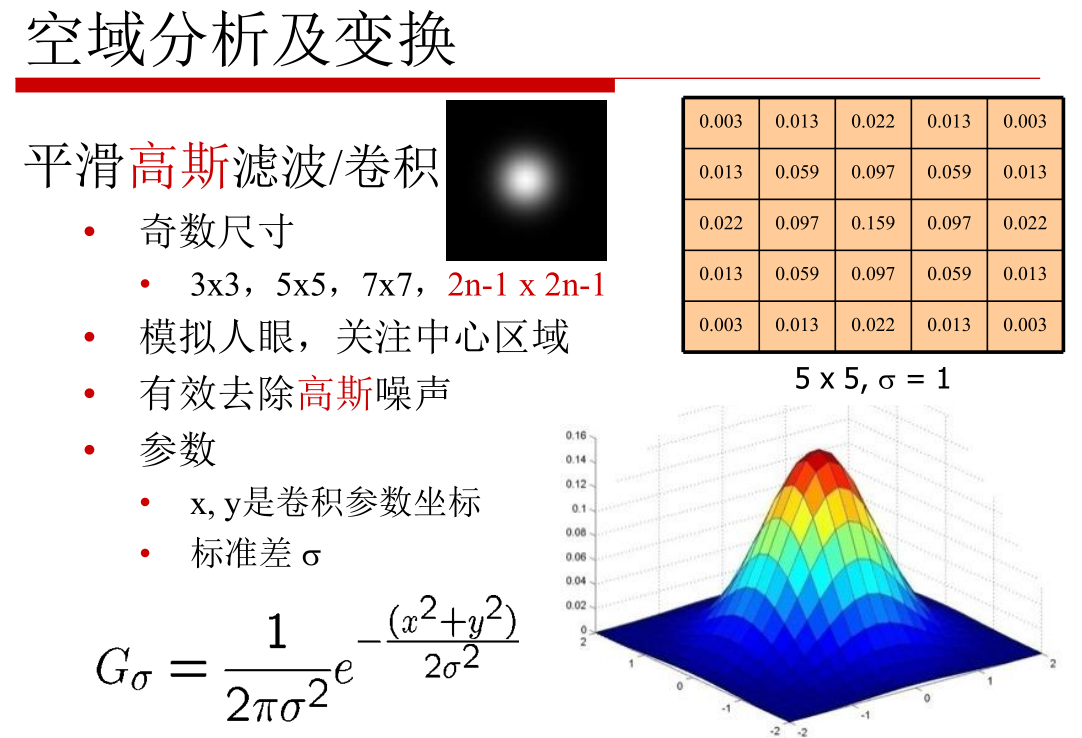


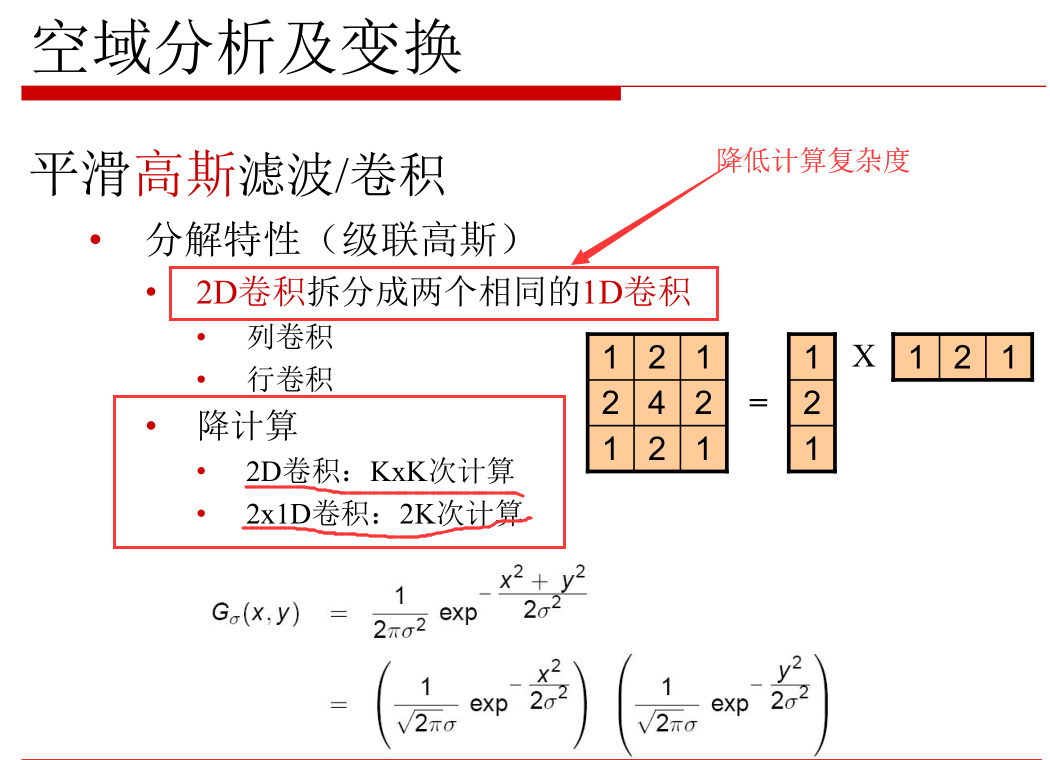
还有一些做边缘检测,团块检测,Laplacian 滤波锐化等滤波器,这里不做一一介绍,详情参考PPT
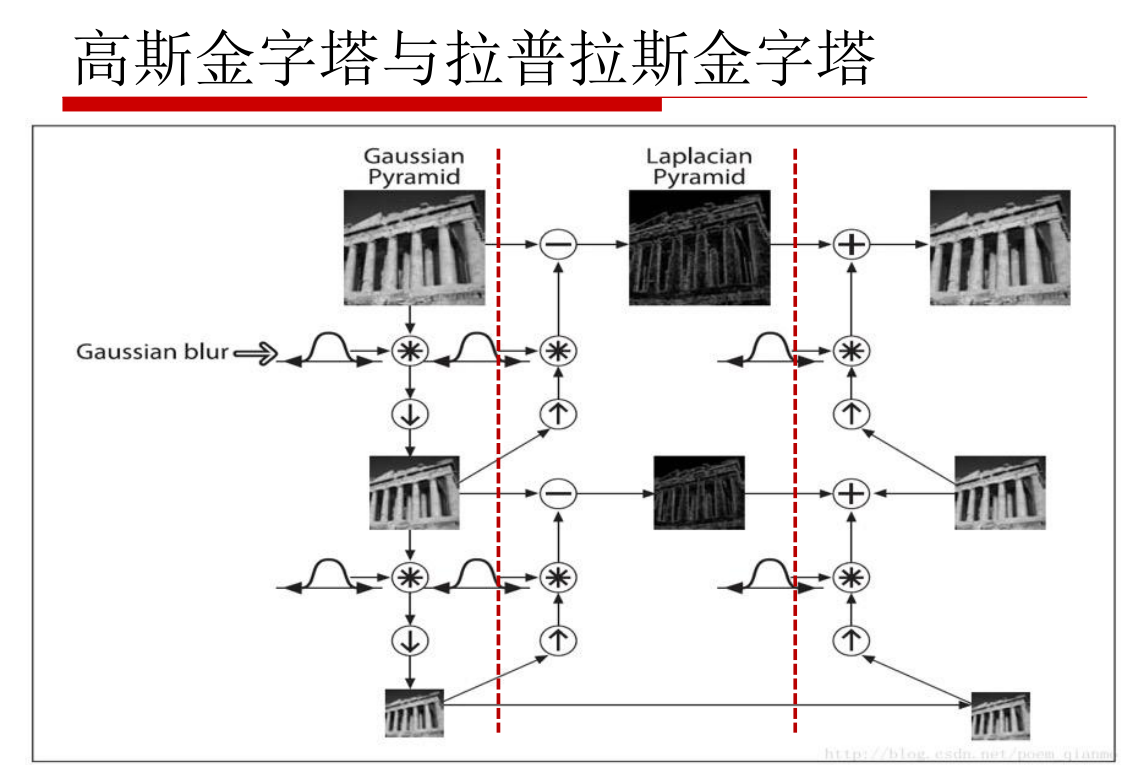
直接进入重点:高斯金字塔
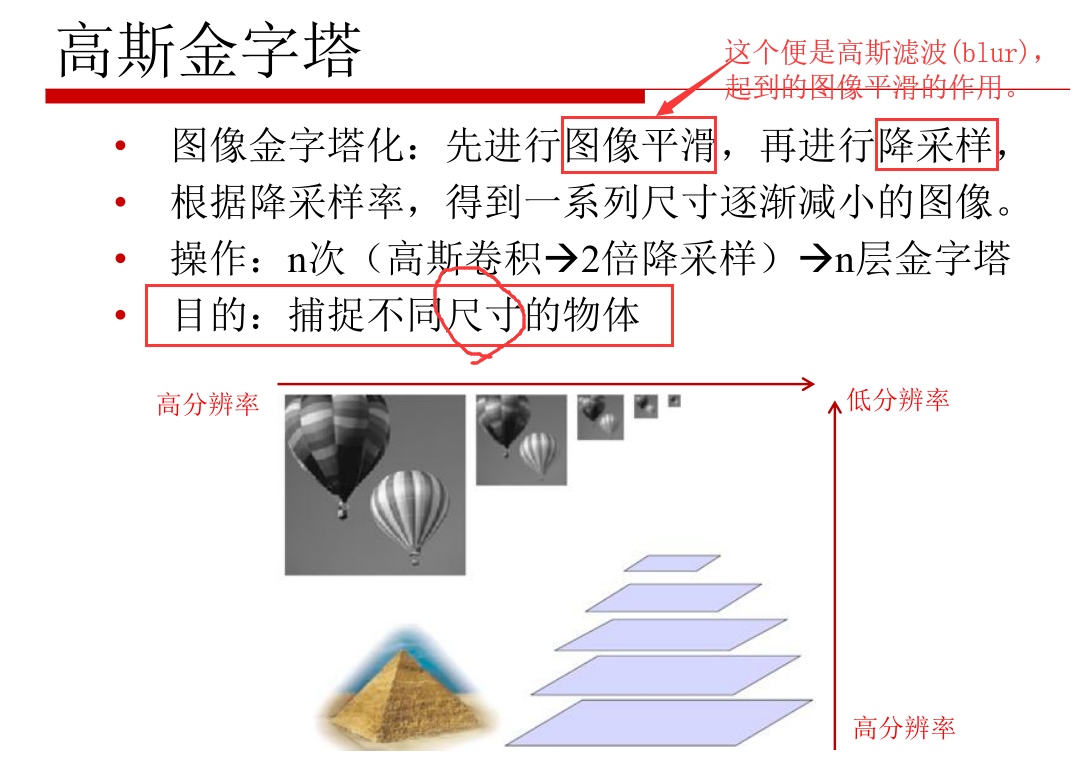

高斯金字塔:通过高斯平缓(模糊) + 降采样(尺寸缩小), 达到捕捉不同尺寸物体的目的。但是如果还想回复原图像怎么办,这就需要拉普拉斯金字塔啦。
拉普拉斯金字塔:将小尺寸的图像数据,进行上采样,得到大尺寸的图像。具体看下图中的说明: