B
Content
· 题目回溯
· 题目分析
· 可行代码
· 总结
(一) 题目回溯
DESCRIPTION

INPUT

OUTPUT

EXAMPLE
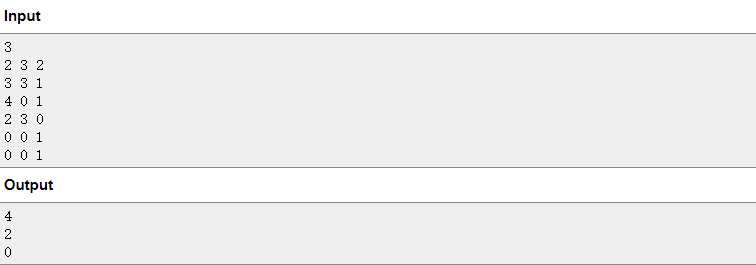
NOTE

(二) 题目分析
目的:将a组中a[0]个 0 与a[1]个 1 与a[2]个 2 和 b组中b[0]个 0 与b[1]个 1 与b[2]个 2通过关系式Ci各项组合的结果相加得到一个总和
令最终总和为sum
Ci的特征:每一项组合的结果只有三种,分别为2,0,-2,所以只需要保证2最多、-2最少即可,即(2,1)多、(1,2)少
解题思路:
1. 将所有(2,1)组合拿出,并且将使用过的a[2]与b[1]减去 .
2. 尽可能减少a[1]、b[2],所以用b[0]与b[2]减去a[1]、用a[0]与a[2]减去b[2] .
3. 由于除a[1]和b[2]外每一个数都已经被使用,又因为两组数字的数量相等,所以最终a[1]和b[2]一定相等 .
4. 将 1 中的正数减去 3 的负数,就是最终的结果sum
(三) 可行代码
1 #include <iostream> 2 #include <math.h> 3 using namespace std; 4 void input(int *arr) 5 { 6 for (int i = 0; i < 3; i++) 7 cin >> arr[i]; 8 return; 9 } 10 int main() 11 { 12 int T; 13 cin >> T; 14 while (T--) 15 { 16 int a[3], b[3]; 17 input(a), input(b); 18 int sum = 0; 19 a[2] >= b[1] ? (sum = 2 * b[1], a[2] -= b[1], b[1] = 0) : (sum = 2 * a[2], b[1] -= a[2], a[2] = 0); // 对应步骤 1 20 (a[1] -= b[0] + b[1]) > 0 ? ((b[2] -= a[0] + a[2]) > 0 ? sum -= 2 * b[2] : 0) : 0; // 对应步骤 3 21 cout << sum << endl; 22 } 23 return 0; 24 }
(四) 总结
对于这类求最大值的题目应该先考虑,找出最大值,然后找影响最大值的因素,具体体现为通过各种限制条件使负数尽可能的少。