大津法(OTSU)是一种确定图像二值化分割阈值的算法,由日本学者大津于1979年提出。从大津法的原理上来讲,该方法又称作最大类间方差法,因为按照大津法求得的阈值进行图像二值化分割后,前景与背景图像的类间方差最大(何为类间方差?原理中有介绍)。
原理:
对于图像I(x,y),前景(即目标)和背景的分割阈值记作T,属于前景的像素点数占整幅图像的比例记为ω0,其平均灰度μ0;背景像素点数占整幅图像的比例为ω1,其平均灰度为μ1。图像的总平均灰度记为μ,类间方差记为g。
假设图像的背景较暗,并且图像的大小为M×N,图像中像素的灰度值小于阈值T的像素个数记作N0,像素灰度大于阈值T的像素个数记作N1,则有:
ω0=N0/ M×N (1)
ω1=N1/ M×N (2)
N0+N1=M×N (3)
ω0+ω1=1 (4)
μ=ω0*μ0+ω1*μ1 (5)
g=ω0(μ0-μ)^2+ω1(μ1-μ)^2 (6)
将式(5)代入式(6),得到等价公式:
g=ω0ω1(μ0-μ1)^2 (7) 这就是类间方差
采用遍历的方法得到使类间方差g最大的阈值T,即为所求。
matlab函数:
matlab中函数graythresh既是使用大津法求得分割阈值T。用法如下:
T = graythresh(img);
BW = im2bw(img,T);
大津法的形象理解:
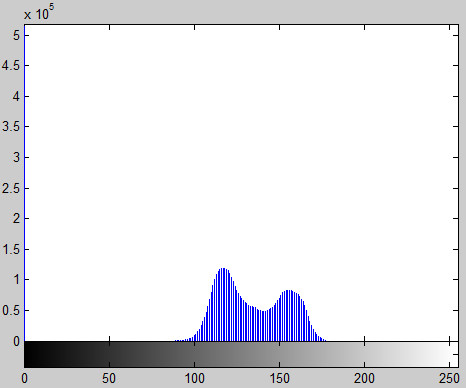
对于直方图有两个峰值的图像,大津法求得的T近似等于两个峰值之间的低谷。
imhist(img);
T = graythresh(img);