转载

本文翻译自A guide to receptive field arithmetic for Convolutional Neural Networks（可能需要翻墙才能访问），方便自己学习和参考。若有侵权，还请告知。

感受野（receptive field）可能是卷积神经网络（Convolutional Neural Network，CNNs）中最重要的概念之一，值得我们关注和学习。当前流行的物体识别方法的架构大都围绕感受野的设计。但是，当前并没有关于CNN感受野计算和可视化的完整指南。本教程拟填补空白，介绍CNN中特征图的可视化方法，从而揭示感受野的原理以及任意CNN架构中感受野的计算。我们还提供了代码实现证明计算的正确性，这样大家可以从感受野的计算开始研究CNN，从而更加深刻的理解CNN的架构。

本文假设读者已经熟悉CNN的思想，特别是卷积（convolutional）和池化（pooling）操作，当然你可以参考[1603.07285] A guide to convolution arithmetic for deep learning，回顾CNN的相关知识。如果你对CNNs已经有所了解，相信不超过半个小时就可以完成本文的阅读。实际上，本文受上述论文的启发，文中也采用了相似的表示符号。

The fixed-sized CNN feature map visualization

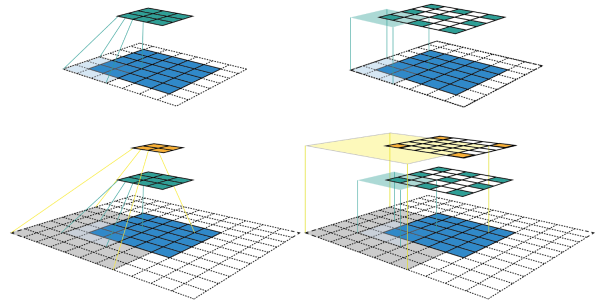
图1 CNN特征图可视化的两种方式。

如图1所示，我们采用卷积核C的核大小（kernel size）k=3*3，填充大小（padding size）p=1*1，步长（stride）s=2*2。（图中上面一行）对5*5的输入特征图进行卷积生成3*3的绿色特征图。（图中下面一行）对上面绿色的特征图采用相同的卷积操作生成2*2的橙色特征图。（图中左边一列）按列可视化CNN特征图，如果只看特征图，我们无法得知特征的位置（即感受野的中心位置）和区域大小（即感受野的大小），而且无法深入了解CNN中的感受野信息。（图中右边一列）CNN特征图的大小固定，其特征位置即感受野的中心位置。

感受野表示输入空间中一个特定CNN特征的范围区域（The receptive field is defined as the region in the input space that a particular CNN’s feature is looking at）。一个特征的感受野可以采用区域的中心位置和特征大小进行描述。图1展示了一些感受野的例子，采用核大小（kernel size）k=3*3，填充大小（padding size）p=1*1，步长（stride）s=2*2的卷积核C对5*5大小的输入图进行卷积操作，将输出3*3大小的特征图（绿色图）。对3*3大小的特征图进行相同的卷积操作，将输出2*2的特征图（橙色）。输出特征图在每个维度上的大小可以采用下面的公式进行计算（[1603.07285] A guide to convolution arithmetic for deep learning）：

为了简单，本文假设CNN的架构是对称的，而且输入图像长宽比为1，因此所有维度上的变量值都相同。若CNN架构或者输入图像不是对称的，你也可以分别计算每个维度上的特征图大小。如图1所示，左边一列展示了一种CNN特征图的常见可视化方式。这种可视化方式能够获取特征图的个数，但无法计算特征的位置（感受野的中心位置）和区域大小（感受野尺寸）。图1右边一列展示了一种固定大小的CNN特征图可视化方式，通过保持所有特征图大小和输入图大小相同来解决上述问题，接下来每个特征位于其感受野的中心。由于特征图中所有特征的感受野尺寸相同，我们就可以非常方便画出特征对应的包围盒（bounding box）来表示感受野的大小。因为特征图大小和输入图像相同，所以我们无需将包围盒映射到输入层。

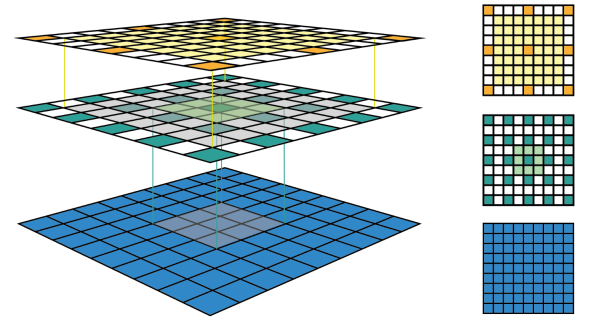
图2 另外一种固定大小的CNN特征图表示。采用相同的卷积核C对7*7大小的输入图进行卷积操作，这里在特征中心周围画出了感受野的包围盒。为了表达更清楚，这里忽略了周围的填充像素。固定尺寸的CNN特征图可以采用3D（左图）或2D（右图）进行表示。

图2展示了另外一个例子，采用相同的卷积核C对7*7大小的输入图进行卷积操作。这里给出了3D（左图）和2D（右图）表示下的固定尺寸CNN特征图。注意：图2中感受野尺寸逐渐扩大，第二个特征层的中心特征感受野很快就会覆盖整个输入图。这一点对于CNN设计架构的性能提升非常重要。

感受野的计算（Receptive Field Arithmetic）

除了每个维度上特征图的个数，还需要计算每一层的感受野大小，因此我们需要了解每一层的额外信息，包括：当前感受野的尺寸r，相邻特征之间的距离（或者jump）j，左上角（起始）特征的中心坐标start，其中特征的中心坐标定义为其感受野的中心坐标（如上述固定大小CNN特征图所述）。假设卷积核大小k，填充大小p，步长大小s，则其输出层的相关属性计算如下：

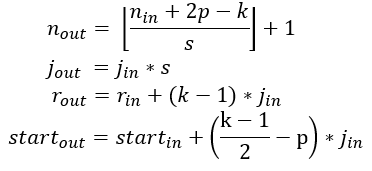
• 公式一基于输入特征个数和卷积相关属性计算输出特征的个数
• 公式二计算输出特征图的jump，等于输入图的jump与输入特征个数（执行卷积操作时jump的个数，stride的大小）的乘积
• 公式三计算输出特征图的receptive field size，等于k个输入特征覆盖区域加上边界上输入特征的感受野覆盖的附加区域。
• 公式四计算第一个输出特征的感受野的中心位置，等于第一个输入特征的中心位置，加上第一个输入特征位置到第一个卷积核中心位置的距离，再减去填充区域大小。注意：这里都需要乘上输入特征图的jump，从而获取实际距离或间隔。

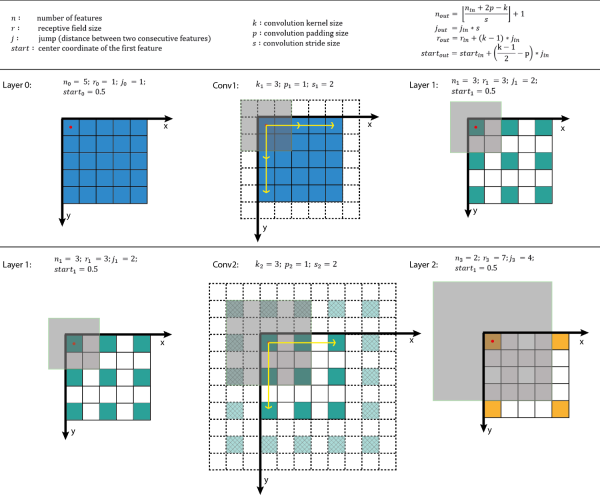
图3 对图1中的例子执行感受野计算。第一行给出一些符号和等式；第二行和最后一行说明给定输入层信息下输出层感受野的计算过程。

CNN的第一层是输入层，n = image size，r = 1，j = 1，start = 0.5。图3采用的坐标系中输入层的第一个特征中心位置在0.5。递归执行上述四个公式，就可以计算CNN中所有特征图中的感受野信息。图3给出这些公式计算的样例。

这里给出一个python小程序，用于计算给定CNN架构下所有层的感受野信息。程序允许输入任何特征图的名称和图中特征的索引号，输出相关感受野的尺寸和位置。图4给出AlexNet下的例子。

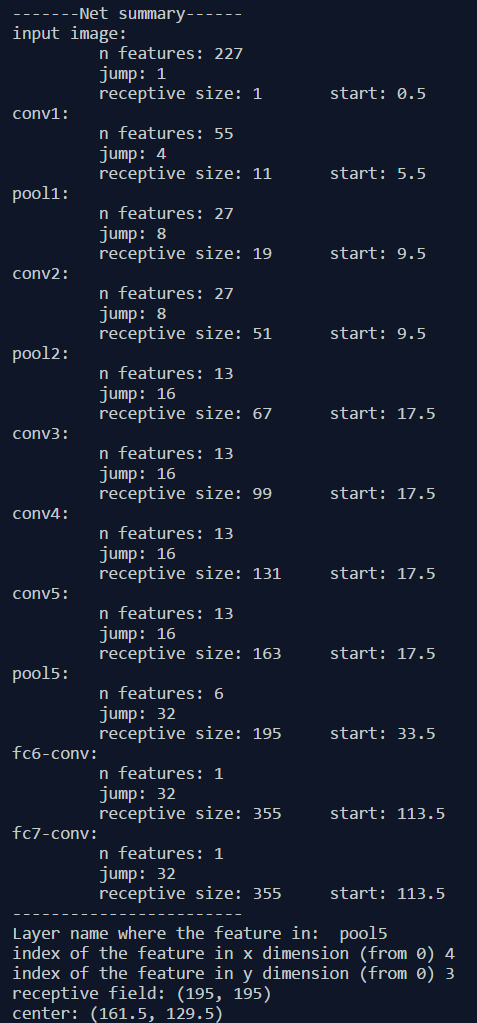
图4 AlexNet下感受野计算样例：

# [filter size, stride, padding]
#Assume the two dimensions are the same
#Each kernel requires the following parameters:
# - k_i: kernel size
# - s_i: stride
# - p_i: padding (if padding is uneven, right padding will higher than left padding; "SAME" option in tensorflow)
# 
#Each layer i requires the following parameters to be fully represented: 
# - n_i: number of feature (data layer has n_1 = imagesize )
# - j_i: distance (projected to image pixel distance) between center of two adjacent features
# - r_i: receptive field of a feature in layer i
# - start_i: position of the first feature's receptive field in layer i (idx start from 0, negative means the center fall into padding)

import math
convnet =   [[11,4,0],[3,2,0],[5,1,2],[3,2,0],[3,1,1],[3,1,1],[3,1,1],[3,2,0],[6,1,0], [1, 1, 0]]
layer_names = ['conv1','pool1','conv2','pool2','conv3','conv4','conv5','pool5','fc6-conv', 'fc7-conv']
imsize = 227

def outFromIn(conv, layerIn):
  n_in = layerIn[0]
  j_in = layerIn[1]
  r_in = layerIn[2]
  start_in = layerIn[3]
  k = conv[0]
  s = conv[1]
  p = conv[2]
  
  n_out = math.floor((n_in - k + 2*p)/s) + 1
  actualP = (n_out-1)*s - n_in + k 
  pR = math.ceil(actualP/2)
  pL = math.floor(actualP/2)
  
  j_out = j_in * s
  r_out = r_in + (k - 1)*j_in
  start_out = start_in + ((k-1)/2 - pL)*j_in
  return n_out, j_out, r_out, start_out
  
def printLayer(layer, layer_name):
  print(layer_name + ":")
  print("	 n features: %s 
 	 jump: %s 
 	 receptive size: %s 	 start: %s " % (layer[0], layer[1], layer[2], layer[3]))
 
layerInfos = []
if __name__ == '__main__':
#first layer is the data layer (image) with n_0 = image size; j_0 = 1; r_0 = 1; and start_0 = 0.5
  print ("-------Net summary------")
  currentLayer = [imsize, 1, 1, 0.5]
  printLayer(currentLayer, "input image")
  for i in range(len(convnet)):
    currentLayer = outFromIn(convnet[i], currentLayer)
    layerInfos.append(currentLayer)
    printLayer(currentLayer, layer_names[i])
  print ("------------------------")
  layer_name = raw_input ("Layer name where the feature in: ")
  layer_idx = layer_names.index(layer_name)
  idx_x = int(raw_input ("index of the feature in x dimension (from 0)"))
  idx_y = int(raw_input ("index of the feature in y dimension (from 0)"))
  
  n = layerInfos[layer_idx][0]
  j = layerInfos[layer_idx][1]
  r = layerInfos[layer_idx][2]
  start = layerInfos[layer_idx][3]
  assert(idx_x < n)
  assert(idx_y < n)
  
  print ("receptive field: (%s, %s)" % (r, r))
  print ("center: (%s, %s)" % (start+idx_x*j, start+idx_y*j))

三个3*3卷积核叠加作用（感受野）等于一个7*7卷积核，但是前者参数更少。

3个3*3：

1个7*7：

参考：

卷积神经网络中的感受野计算（译）

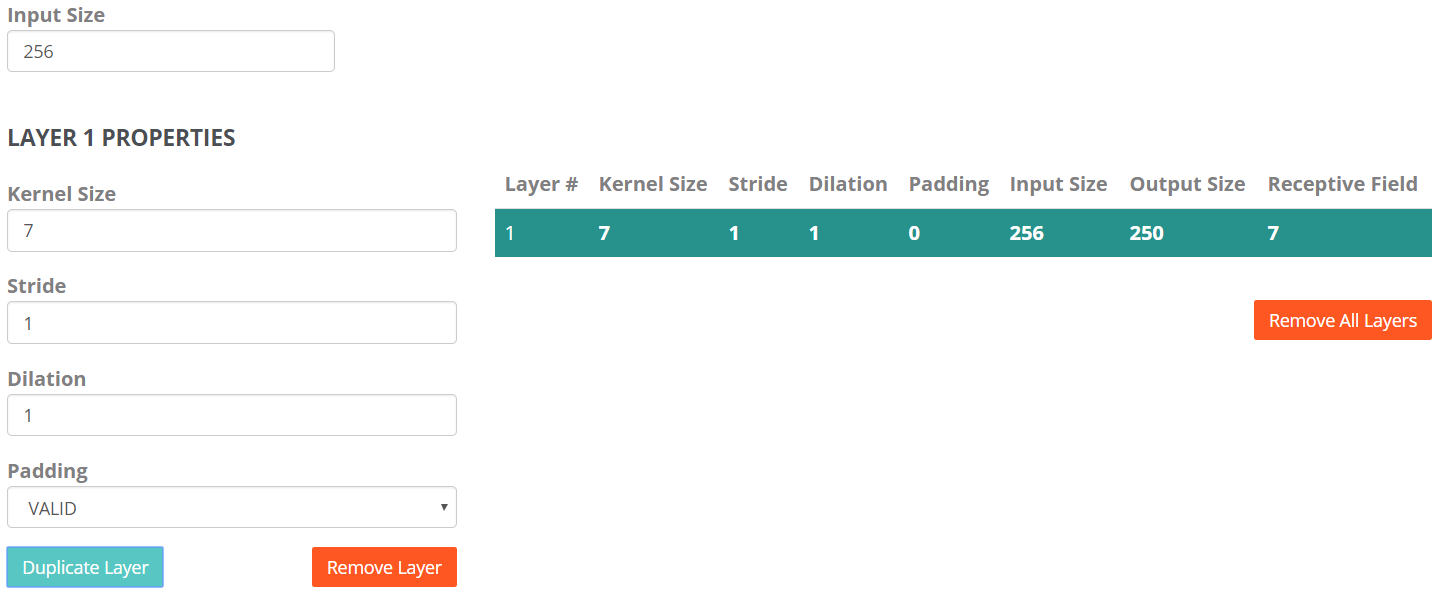
RECEPTIVE FIELD CALCULATOR  一个可以计算任意层感受野的网站

5*5卷积核替换为两个级联3*3卷积核在参数和计算量上的影响

卷积神经网络的卷积核大小、卷积层数、每层map个数都是如何确定下来的呢？ 

动图：github