逻辑回归
1. 逻辑回归(Logistic Regression)
逻辑回归虽然叫逻辑回归,但是它是一个用来分类的模型
2. 二分类问题(Binary Classification)
在回归问题中,输出的是连续值,在二分类问题中,输出值(y)只有(0,1)两种取值,即(yin {0,1}),其中(0)代表负类,(1)表示正类
一种简单的办法就是用线性回归的模型来做分类,但是效果不是很好,因为分类问题不符合线性关系
3. 假设函数
在线性回归任务中,用的假设函数是:
[h_{ heta}(x) = heta^T x
]
需要一个满足(0 le h_{ heta}(x) le 1) 的假设函数,即
[0 le h_{ heta}(x) = g( heta^Tx) le 1
]
当然最简单的函数就是阶跃函数:
[g(z) = �egin{cases} 1 & z > 0 \ frac12 & z=0 \ 0 & z < 0 end{cases}
]
[其中z = heta^T x
]
但是阶跃函数不可微,所以一般常用的是(sigmoid)函数,也可以叫(logistic)函数
[g(z) = frac1{1+e^{-z}}
]
[�egin{cases} lim_{z
ightarrow -infty}g(z) = 0 \ g(0) = 0.5 \ lim_{z
ightarrow +infty}g(z) = 1 end{cases}
]
函数图像是这样的
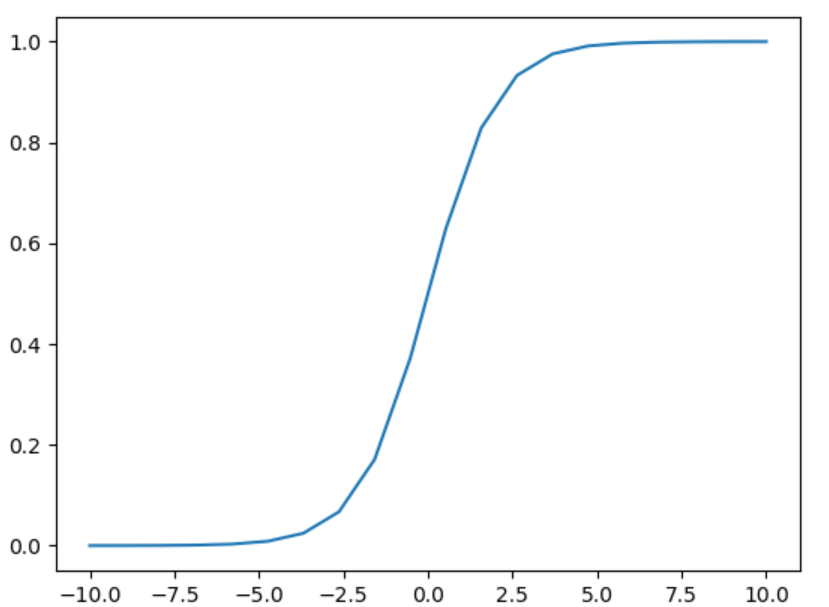
(logistic)函数可以把任意一个实数映射到((0,1))区间内,而且还是一个可微函数,同时可以定义(h_{ heta}(x))为输入特征分类到正类的概率,即:
[h_{ heta}(x) = P(y = 1mid x; heta)
]
表示输入为(x)且参数为( heta)的情况下分为正类的概率,且
[P(y = 1mid x; heta) + P(y = 0mid x ; heta) = 1
]
4. 决策边界(Decision Boundary)
根据(logistic)函数,可以根据概率得出分类,即
[y = �egin{cases} 1 & h_{ heta}(x) ge 0.5 \ 0 & h_{ heta}(x) < 0.5 end{cases}
]
又因为:
[h_{ heta}(x) = g( heta^{T} x) = frac{1}{1 + e^{ heta^Tx}}
]
可以得出
[y = �egin{cases} 1 & heta^Tx ge 0 \ 0 & heta^Tx < 0 end{cases}
]
而决策边界就是一条线,把整个区域分为了两部分,对于两个特征的分类模型,这里的决策边界可以是( heta_0 + heta_1 x_1 + heta_2 x_2 = 0),如果( heta_0 + heta_1 x_1 + heta_2 x_2ge0)就分为正类, 否则分为负类
决策边界和( heta^Tx)有关,当( heta^Tx)不是线性的时候,决策边界就不是一条直线了
5. 代价函数(Cost Function)
在线性回归中,使用的代价函数是平方损失函数,而在逻辑回归中不能用平方损失函数来作为代价函数,因为在分类任务中平方损失函数是非凸的,也就是有多个局部最小值。所以在逻辑回归中采取的代价函数是这样的:
[J( heta) = frac1m sum_{i=1}^m Cost(h_{ heta}(x^{(i)}),y^{(i)} ) )
]
[Cost(h_{ heta}(x^{(i)}),y^{(i)} ) = �egin{cases}-log(h_{ heta}(x^{(i)})) & y^{(i)} = 1 \ -log(1-h_{ heta}(x^{(i)})) & y^{(i)} = 0 end{cases}
]
且这个代价函数满足:
[Cost(h_{ heta}(x^{(i)}),y^{(i)} ) = �egin{cases} 0 & h_{ heta}(x^{(i)}) = y^{(i)} \ infty & h_{ heta}(x^{(i)})=1 And y^{(i)} = 0 \ infty & h_{ heta}(x^{(i)})=0 And y^{(i)} = 1 end{cases}
]
图像如下:
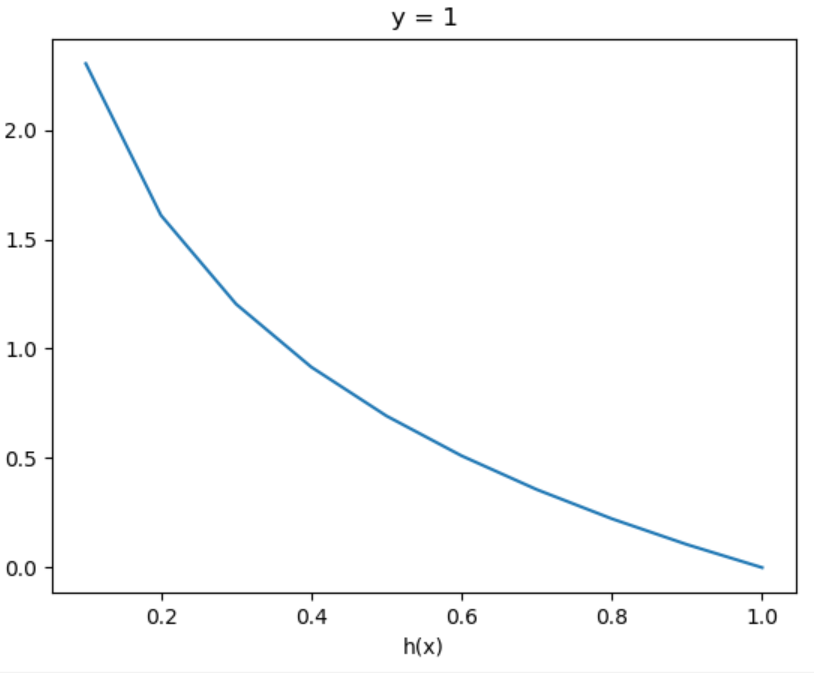
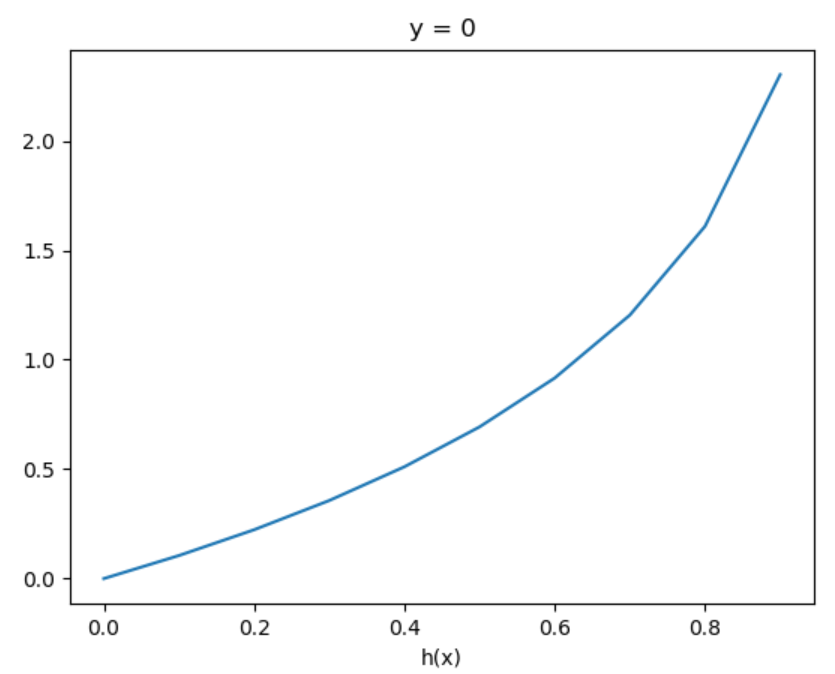
在这样定义的代价函数下损失函数 (J( heta)) 是凸的,也就是只有一个局部最小值
为了方便表示,上面的代价函数等价于:
[Cost(h_{ heta}(x^{(i)}),y^{(i)} ) = -y^{(i)}log(h_{ heta}(x^{(i)})) -(1-y^{(i)})log(1-h_{ heta}(x^{(i)}))
]
所以最终逻辑回归的损失函数定义如下:
[J( heta) = frac1msum_{i=1}^m (-y^{(i)}log(h_{ heta}(x^{(i)})) -(1-y^{(i)})log(1-h_{ heta}(x^{(i)})))
]
实际上这个就是对概率论中的最大似然估计函数取了负均值
6. 梯度下降(Gradient Decent)
梯度下降这方面的公式和线性回归是一样的
[frac{partial}{partial heta_j}J( heta) = frac{1}{m} sum_{i=1}^m (h_{ heta}(x^{(i)})) - y^{(i)})x^{(i)}_j
]
梯度下降迭代更新公式为:
[ heta_j := heta_j - frac{alpha}{m} sum_{i=1}^m (h_{ heta}(x^{(i)})) - y^{(i)})x^{(i)}_j
]
向量化之后就是:
[ heta := heta - frac{alpha}{m}X^T(g(X heta) - y)
]
7. 多分类任务(Multiclass Classification)
对于有多个标签类别的分类任务,采用One vs all的方法来做
假设类别(yin{0,1,cdots,n}),对于每一类别(c),把该类别的输入当作正类,把所有其他类别的输入当作负类,然后进行一次二分类模型的构建,最终得到(n+1)个模型,然后对于一个输入,其预测值就是各个分类器中分为正类概率最大的那一个
[yin {0,1,cdots,n}
]
[h_{ heta}^{(0)} = P(y = 0mid x; heta)
]
[h_{ heta}^{(1)} = P(y = 0mid x; heta)
]
[cdots
]
[h_{ heta}^{(n)} = P(y = 0mid x; heta)
]
[prediction = mathop{argmax}limits_{i}(h_{ heta}^{(i)})
]


