题意:
给出一个图,边是有向的,现在给出一些边的变化的信息(权值大于原本的),问经过这些变换后,MST总权值的期望,假设每次变换的概率是相等的。
思路:
每次变换的概率相等,那么就是求算术平均。
首先求出最小生成树,若变换的边不在最小生成树上,那么就不用管;如果在,那么就需要求变换之后的MST的总权值,有两种情况,第一是继续使用变换后的边,还是MST,第二是放弃这条边,使用其它边构成MST。取两者中的最小值。
第二种情况需要较为深入的讨论,如何使得在较优的时间内找到一条边,使得这条边加入后还是MST。
放弃了一条边之后,MST就变成了两棵最小生成子树,那么要找的边实际就是两棵树之间的最短距离,就转化成了求两棵树之间的最短距离。
如何求两棵树的最短距离,树形dp,这个我也是看题解学习的Orz。具体的做法是每次用一个点作为根,在dfs的过程中,将每一条非树边对最短距离进行更新,这个最短距离对应的是去掉dfs中每一对点所连的边的形成的两棵子树。
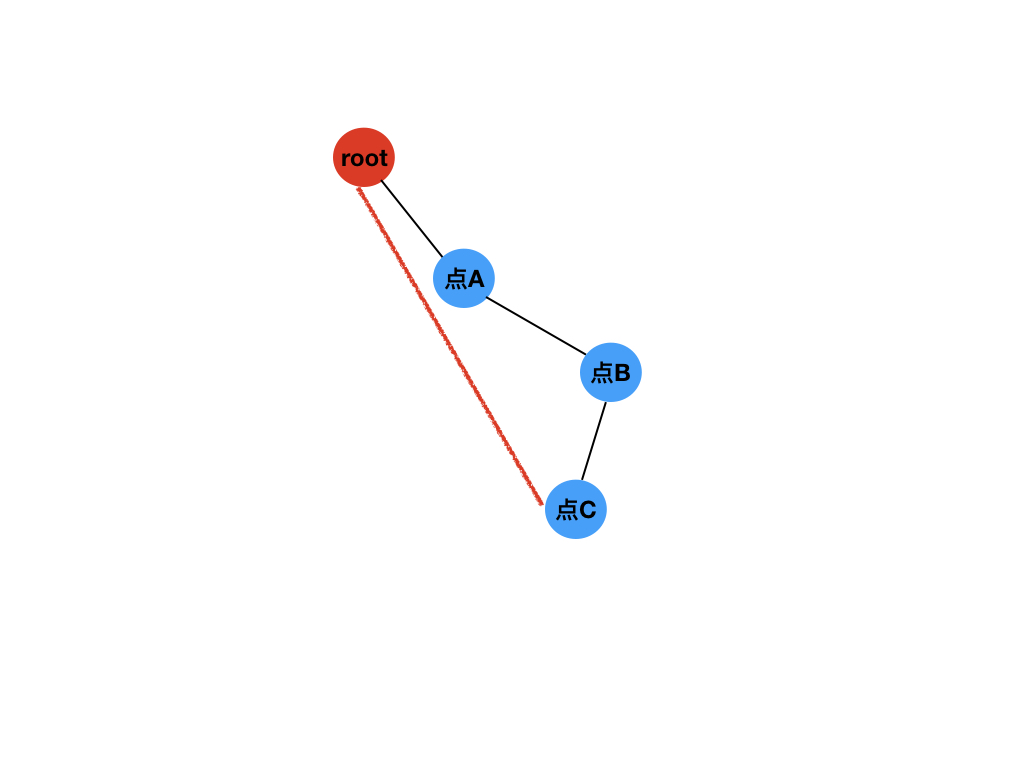
看图
红色的是非树边,那么这条非树边就可以更新去掉点A与点B连的树边之后形成的两棵树的最小距离,也可以更新去掉点B与点C连的树边后形成的两棵树的最小距离。每次dfs访问n个点,n次dfs,所以复杂度为O(n^2)。
总复杂度为O(n^2)。
代码:
1 #include <stdio.h> 2 #include <string.h> 3 #include <algorithm> 4 #include <vector> 5 using namespace std; 6 7 const int N = 3005; 8 const int inf = 0x3f3f3f3f; 9 10 int mp[N][N],pre[N]; 11 bool used[N][N]; 12 int dp[N][N]; 13 int vis[N]; 14 int d[N]; 15 vector<int> g[N]; 16 17 struct edge 18 { 19 int to,cost; 20 21 edge(int a,int b) 22 { 23 to = a; 24 cost = b; 25 } 26 }; 27 28 long long prim(int n) 29 { 30 memset(vis,0,sizeof(vis)); 31 memset(used,0,sizeof(used)); 32 //memset(path,0,sizeof(path)); 33 34 for (int i = 0;i < n;i++) g[i].clear(); 35 36 vis[0] = 1; 37 d[0] = 0; 38 39 for (int i = 1;i < n;i++) 40 { 41 d[i] = mp[0][i]; 42 pre[i] = 0; 43 } 44 45 int ans = 0; 46 47 for (int i = 0;i < n - 1;i++) 48 { 49 int x; 50 int dis = inf; 51 52 for (int j = 0;j < n;j++) 53 { 54 if (!vis[j] && d[j] < dis) 55 { 56 x = j; 57 dis = d[j]; 58 } 59 } 60 61 vis[x] = 1; 62 63 used[x][pre[x]] = used[pre[x]][x] = 1; 64 65 g[x].push_back(pre[x]); 66 g[pre[x]].push_back(x); 67 68 ans = ans + dis; 69 70 for (int j = 0;j < n;j++) 71 { 72 //if (vis[j] && j != x) path[x][j] = path[j][x] = max(dis,path[j][pre[x]]); 73 74 if (!vis[j] && mp[x][j] < d[j]) 75 { 76 d[j] = mp[x][j]; 77 pre[j] = x; 78 } 79 } 80 } 81 82 return ans; 83 } 84 85 int dfs(int root,int u,int fa) 86 { 87 int s = inf; 88 89 for (int i = 0;i < g[u].size();i++) 90 { 91 int v = g[u][i]; 92 93 if (v == fa) continue; 94 95 int tmp = dfs(root,v,u); 96 97 s = min(tmp,s); 98 99 dp[u][v] = dp[v][u] = min(dp[u][v],tmp); 100 } 101 102 if (root != fa) 103 s = min(s,mp[root][u]); 104 105 return s; 106 } 107 108 void solve(int n) 109 { 110 memset(dp,inf,sizeof(dp)); 111 112 for (int i = 0;i < n;i++) 113 { 114 dfs(i,i,-1); 115 } 116 } 117 118 119 int main() 120 { 121 int n,m; 122 123 while (scanf("%d%d",&n,&m) != EOF) 124 { 125 if (m == 0 && n == 0) break; 126 127 memset(mp,inf,sizeof(mp)); 128 129 for (int i = 0;i < n;i++) 130 { 131 g[i].clear(); 132 } 133 134 for (int i = 0;i < m;i++) 135 { 136 int a,b,c; 137 138 scanf("%d%d%d",&a,&b,&c); 139 140 mp[a][b] = mp[b][a] = c; 141 142 //G[a].push_back(edge(b,c)); 143 //G[b].push_back(edge(a,c)); 144 } 145 146 int ans = prim(n); 147 148 solve(n); 149 150 //printf("ans = %d ",ans); 151 152 int q; 153 154 scanf("%d",&q); 155 156 long long res = 0; 157 158 for (int i = 0;i < q;i++) 159 { 160 int x,y,c; 161 162 scanf("%d%d%d",&x,&y,&c); 163 164 if (!used[x][y]) res += ans; 165 else 166 { 167 long long tmp = (long long)ans + c - mp[x][y]; 168 169 //printf("%d ** ",dp[x][y]); 170 171 tmp = min(tmp,(long long)ans + dp[x][y] - mp[x][y]); 172 173 res += tmp; 174 175 //printf("%d %lld** ",dp[x][y],tmp); 176 } 177 } 178 179 printf("%.4f ",(double) res / q); 180 } 181 182 return 0; 183 }