移动平均法可以作为一种数据平滑的方式,以每天的气温数据为例,今天的温度可能与过去的十天的温度有线性关系;或者做的饭一部分是上顿的,一部分是现在的,再假设隔两顿的都被倒掉了,并且每天都是这样的,这就是一个一阶的移动平均。
1. 移动平均法
移动平均法根据时间序列逐渐推移,依次计算包含一定项数的时序平均数,以反映长期趋势的方法。当时间序列的数值由于受周期变动和不规则变动的影响,起伏较大,不易显示出发展趋势时,可用移动平均法,消除这些因素的影响,分析、预测序列的长期趋势。移动平均法有简单移动平均法、加权移动平均法、趋势移动平均法。
2. 简单移动平均法

近N期序列值的平均值作为未来各期的预测结果。一般N的取值范围:5≤N≤200。当历史序列的基本趋势变化不大且序列中随机变动成分较多时,N的取值应该大一些。否则N的取值应小一些。在有确定的季节变动周期的资料中,移动平均的项数应取周期长度。选择最佳N的方法是,比较若干模型的预测误差。预测标准误差小者为好。
简单移动平均法只适合做近期预测,而且预测目标的发展趋势变化不大。如果目标的发展趋势存在其它变化,采用简单移动平均法就会产生较大的预测偏差和滞后。
例1:某企业1-11月份的销售收入时间序列如表1所示。试用一次简单移动平均法预测第12月份的销售收入。
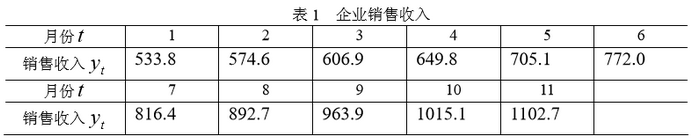

 958.2,预测的标准误差为:
958.2,预测的标准误差为:
 182.4
182.4
计算表明,N = 4时,预测的标准误差较小,所以选取N = 4。预测第12月份的销售金额为993.6。
3. 加权移动平均法
在简单移动平均公式中,每期数据在求平均时的作用是等同的。但是,每期数据所包含的信息量不一样,近期数据包含着更多关于未来情况的信息。因此,把各期数据等同看待是不合理的,应考虑各期数据的重要性,对近期数据给予较大的权重,这就是加权移动平均法的基本思想。

例2:我国1979-1988年原煤产量如表2所示,试用加权移动平均法预测1989年的产量。

在加权移动平均法中,wt 选择的原则是:近期数据的权数大,远期数据的权数小。
4. 趋势移动平均法
简单移动均值法和加权移动平均法,在时间序列没有明显的趋势变动,反映实际情况。但当时间序列出现直线增加或减少的变动趋势时,这两种方法出现滞后偏差。因此,需要修正,修正的方法是作二次移动平均,利用移动平均滞后偏差的规律来建立直线趋势的预测模型。这就是趋势移动平均法。一次移动的平均数为


例3:我国1965-1985年的发电量如表3所示,试预测1986年和87年的发电总量。
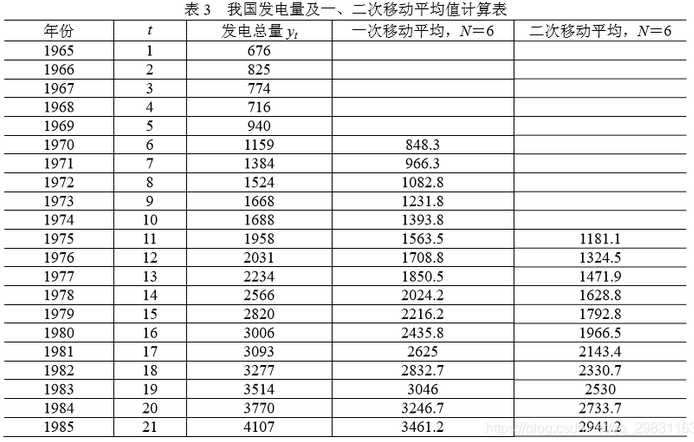
解:由散点图1看出,发电量基本呈现直线上升趋势,可用趋势移动平均法来预测。
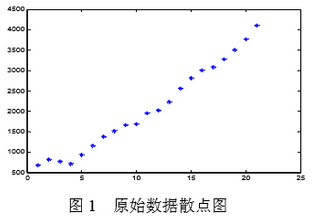

错误:1986年的预测值:3981.1+208 = 4189.1
趋势移动平均法对同时存在直线趋势与周期波动的序列,是一种既能反映趋势变化,又可以有效地分离出周期变动的方法。