支持向量机原理(一) 线性支持向量机、支持向量机原理(二)线性支持向量机的软间隔最大化模型,讲的是SVM的硬间隔最大化和软间隔最大化算,但他们对完全线性不可分没办法。该博客讲述核函数在SVM中处理线性不可分数据的作用。
1. 多项式回归
在线性回归原理中,提到将多项式回归转化为线性回归。
比如:
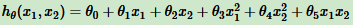
令:

得到:

此时将二元多项式回归转化为五元线性回归。通过二元样本特征得到五元样本特征(x1,x2,x3,x4,x5),即( )
)
这给我们启发,将低维线性不可分映射到高维,变为线性可分。
2. 核函数
线性可分SVM的优化目标函数:

式子中低维特征仅以内积 xi • xj 形式出现,现在定义一个低维特征空间到高维特征空间的映射Ø(比如上一节的2维到5维),得到SVM的优化目标函数:
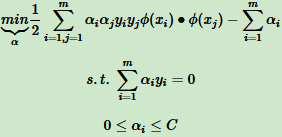
可以看出,和线性可分SVM的优化目标函数的区别:将内积 xi • xj 替换为 Ø(xi)•Ø(xj)。
这种方法看起来解决了线性不可分SVM的问题了。可以将2维映射到5维,3维映射到19维。但低纬如果是100,1000,此时计算量太大,这种方法不合适。
核函数登场
假设Ø是一个从低维的输入空间χ(欧式空间的子集或离散集合)到高维的希尔伯特空间的 Η 映射。如果存在函数 K(x, z) ,对任意 x, z ∈ χ,都有:
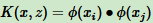
此时称 K(x, z) 为核函数。
核函数将特征从低维映射高维,但核函数计算是在低维上,将实质上的分类效果(利用了内积)表现在高维上。
3. 核函数的介绍
scikit-learn默认的几个核函数:
3.1 线性核函数
线性核函数(Linear Kernel)就是线性可分SVM,表达式:
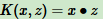
也就是说,线性可分SVM可以和线性不可分SVM归为一类,区别在于线性可分SVM用的是线性核函数。
3.2 多项式核函数
多项式核函数(Polynomial Kernel)表达式:
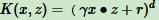
其中,γ,r,d在调参时自己定义。
3.3 高斯核函数
高斯核函数(Gaussian Kernel),也称径向基核函数(Radial Basis Function, RBF),是非线性分类SVM最主流的核函数。libsvm默认的核函数。表达式:
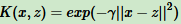
其中,γ>0,调参时自己定义。
3.4 Sigmoid核函数
Sigmoid核函数(Sigmoid Kernel)表达式:
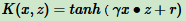
其中,γ,r调参时自己定义。
4. 分类SVM算法小结
此时不再区分是否线性可分。
输入:m个样本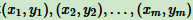 ,其中 x 为 n 维特征向量。γ为二元输出,值为1或-1。
,其中 x 为 n 维特征向量。γ为二元输出,值为1或-1。
输出:分离超平面的参数 ω*,b*和分类决策树函数。
算法过程:
(1)、选择适当的核函数 K(x, z) 和惩罚系数 C>0,构造约束优化问题
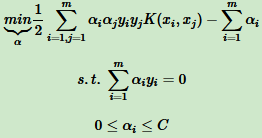
(2)、用SMO算法求出上式最小时对应的α向量的α*向量。
来自:刘建平