SVM压制了神经网络好多年，如果不考虑集成学习算法，不考虑特定的训练集，在分类算法中SVM表现排第一。
SVM是一个二元分类算法。
SVM学习策略：间隔最大化，可形式化为一个求解凸二次规划问题。
间隔最大化使它有别于感知机。
SVM包括核技巧，使它成为非线性分类器。
支持向量机模型包括：线性可分支持向量机、线性支持向量机、非线性支持向量机。当训练集线性可分，通过硬间隔最大化学习的线性分类器为线性可分支持向量机，又称硬间隔支持向量机；通过软间隔最大化学习的线性分类器为线性支持向量机，又称软间隔支持向量机；当训练集线性不可分，通过核技巧及软间隔最大化学习的称为非线性支持向量机。
1. 回顾感知机模型
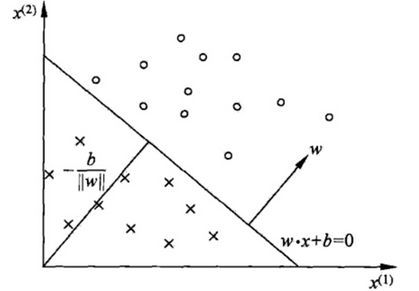
在感知机原理中，在二维就是找到一条直线，在三维或者更高维就是找到一个超平面，将所有二元类别分开。这个超平面定义为：wTx+b=0。如图，在超平面wTx+b=0上方定义y=1，在超平面下方定义y=-1。可以看出满足这个超平面的不止一个。我们尝试找到最好的。
感知机损失函数优化的思想：让所有误分类点(定义为M)到超平面的距离之和最小，即下面式子的最小化：
当w和b扩大N倍，分母L2范数也会扩大N倍。也就是分子，分母有倍数关系。所以可以固定分子或分母为1，然后求分母倒数或另一个分子最小化作为损失函数。感知机模型中，固定分母||w||2=1，则感知机损失函数简化为：
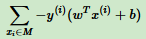
2. 函数间隔与集合间隔
超平面为wTx+b=0，|wTx+b|为点x到超平面的相对距离。当wTx+b与y同号，分类正确，否则，分类不正确。这里引入函数间隔的感念，定义函数间隔 γ’为：
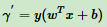
即函数间隔就是感知机模型中误分类点到超平面距离的分子。对于训练集中m个样本点对应的m个函数间隔的最小值，就是整个训练集的函数间隔。
函数间隔并不能正常反应点到超平面的距离，在感知机模型中，分子成比例增长，分母也增长。为了统一度量，对法向量w加上约束条件，得到几何间隔γ为：
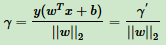
几何间隔是点到超平面的真正距离，感知机模型里用到的距离就是几何距离。
3. 支持向量
感知机利用误分类最小的策略，求得分离超平面有无穷多个；线性可分支持向量机利用间隔最大化求得最优分离超平面只有一个。
如图，线性可分支持向量机：决策边界(实)，间隔边界(虚)，支持向量(红点)。
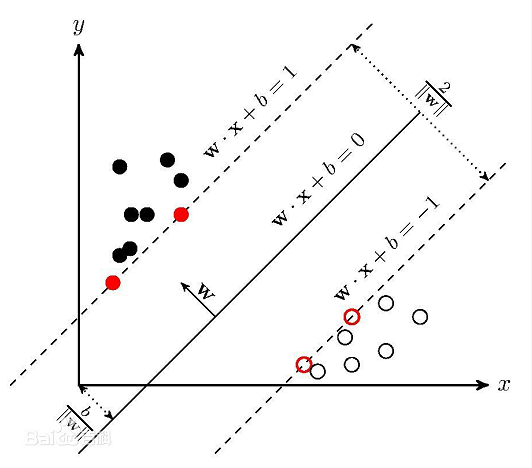
支持向量到超平面的距离为1/||w||2，两个支持向量之间的距离为2/||w||2。
4. SVM模型目标函数与优化
SVM模型：让所有点到超平面的距离大于支持向量到超平面的距离。数学表达式：
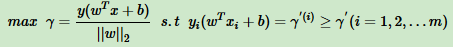
一般取函数间隔r‘为1，表达式变为：
也就是说在约束条件下 yi(wTxi + b)≥1 (i = 1,2,3...m)下，最大化1/||w||2。可以看出，SVM是固定分子优化分母，同时加上支持向量的限制。
由于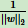
的最大化等同于
最小化。所以SVM的优化函数等价于：
由于目标函数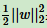
是凸函数，同时约束条件不等式是仿射的，根据凸优化理论，通过拉格朗日函数将优化目标转化为无约束的优化函数，这和最大熵模型原理中讲的目标函数优化方法一样。优化函数转化为：
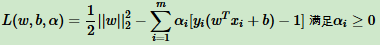
由于引入拉格朗日乘子，优化目标变为：
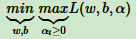
和最大熵模型一样，这个优化函数满足KKT条件，可以通过拉格朗日对偶将优化问题转化为等价的对偶问题。
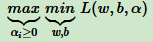
上式中，可以先求优化函数对于 ω 和 b 的极小值。接着再求拉格朗日乘子 α 的极大值。
先求
，对 ω 和 b 分别求偏导：
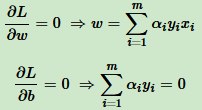
从上面两个式子得到 ω 和 α 的关系，只要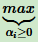
求出 α，就可以求出 ω，至于 b，由于上面两个式子没有 b，所以最后的 b 可以有多个。
求出 ω 和 α 的关系，带入优化函数 L(ω,b,α) 消去 ω。我们定义：
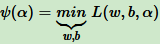
下面是将 ω 替换为 α 的 ψ(α) 表达式：
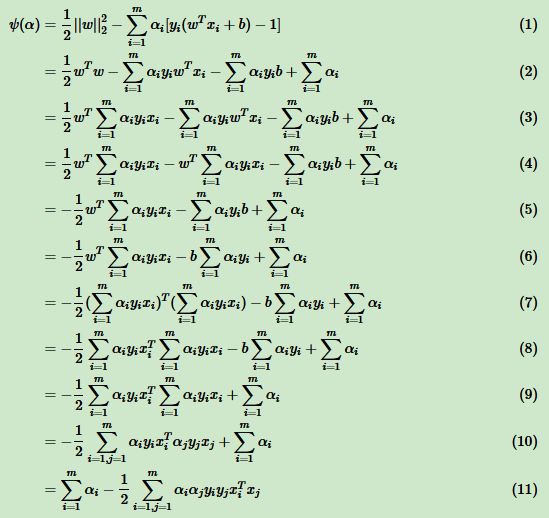
其中，(1)到(2)用到了范数的定义
，(2)到(3)用到了
，(3)到(4)把和样本无关的 ωT 提前，(4)到(5)合并了同类项，(5)到(6)把和样本无关的 b 提前，(6)到(7)继续用，(7)到(8)用到了向量的转置。由于常量的转置是其本身，所以只有向量 xi 被转置，(8)到(9)是用到了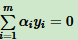
，(9)到(10)用到了
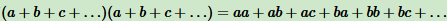的乘法运算，(10)到(11)仅仅是位置的调整。
从上面看出，通过对 ω，b极小化以后，我们的优化函数 ψ(α) 仅仅只有 α 向量做参数。只要能够极大化 ψ(α) ，就可以求出此时对应的 α，进而求出 ω，b。