来自:刘建平
逻辑回归是分类算法,可以处理二元分类和多元分类。
名字里有“回归”二字,但不是回归算法。为什么名字有“回归”这个误导词?因为它的原理有回归模型的影子。
1. 从线性回归到逻辑回归
线性回归模型是求Y和X之间的线性关系系数Θ,满足Y= XΘ。此时Y是连续的,所以是回归模型。
想要Y是离散的话,对Y再做一次函数转换,变为g(Y)。如果g(Y)结果类别是两种,就是二元分类模型。
2. 二元逻辑回归的模型
对线性回归的结果做函数g的转换,变为逻辑回归。g一般取sigmoid函数:
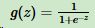
取sigmoid函数,主要因为两个性质:
- 当z趋于正无穷时,g(z)趋于1,当z趋于负无穷,g(z)趋于0。
- (导数性质)
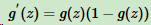
令g(z)中的z为:z = xΘ,得到二元逻辑回归模型一般形式:
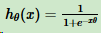
其中x为样本输入,hΘ(x)为模型输出,可以是某一分类的概率大小。hΘ(x)和二元分类样本y(假设为0和1)有这样对应关系,如果hΘ(x)>0.5,即xΘ>0,则y为1。如果hΘ(x)<0.5,即xΘ<0,则y为0。y = 0.5是临界情况,此时xΘ=0,无法确定分类。
hΘ(x)值越小,分类为0的概率越高;值越大,分类为1的概率越高。靠近临界点,分类准确率会下降。
模型的矩阵模式:

其中hΘ(X)为模型输出,m*1维度。X为样本特征矩阵,为m*n维度。Θ为模型系数,为n*1的向量。
3. 二元逻辑回归的损失函数
线性回归是连续的,使用模型误差的平方和来定义损失函数。逻辑回归使用最大似然法定义损失函数。
样本输出是0或1两类,得到:
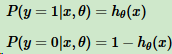
把两个式子写成一个式子:
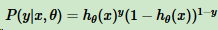
其中y的取值是0或者1。
得到y的概率分布函数,就可以用似然函数最大化求解模型系数Θ。为了方便求解,这里我们用对数似然函数最大化,对数似然函数取反即为损失函数J(θ)。其中,似然函数的代数表达式为:
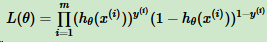
损失函数表达式:
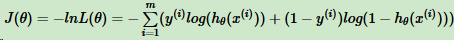
矩阵形式:
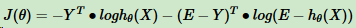
- 为内积。
4. 二元逻辑回归的损失函数的优化方法
损失函数最小化, 最常见的有梯度下降法、坐标轴下降法、等牛顿法。
下面是推到梯度下降法中θ步骤:

5. 二元逻辑回归的正则化
逻辑回归也有过拟合问题,需要正则化,常见的L1正则化和L2正则化。
L1正则化:
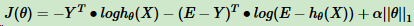
超参数α是惩罚系数,||θ||1为θ的L1范数。
L1正则化损失函数的优化方法常用坐标轴下降法和最小角回归法。
L2正则化:
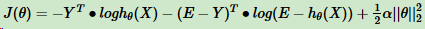
||θ||2为θ的L2范数。
L2正则化损失函数的优化方法和普通的逻辑回归类似(梯度下降法)。
6.小结
逻辑回归尤其是二元逻辑回归,训练速度很快,虽然使用起来没有支持向量机(SVM)占主流,但是解决普通的分类问题是足够了,训练速度比SVM快不少。
hθ(x)
来自:刘建平