从感知机到神经网络
感知机
感知器在20世纪五、六十年代由科学技术Frank Rosenblatt发明,其受到Warren McCulloch和Walter Pitts早期的工作的影响。今天,使用其他人工神经元模型更为普遍———在这本书中,以及更多现代的神经网络工作中,主要使用的是一种叫做S型神经元的神经元模型。
感知器是如何工作的呢?一个感知器接受几个二进制输入,并产生一个二进制输出:
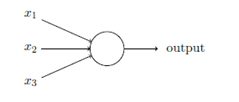
示例中的感知器由三个输入,。通常可以由更多或更少的输入。Rosenblatt提议一个简单的规则来计算输出。他引入权重, 表示相应输入对于输出重要性的实数。神经元的输出,0或者1,则由分配权重后的总和小于或者大于一些阈值决定。和权重一样,阈值是一个实数,一个神经元的参数。用更精确的代数形式:
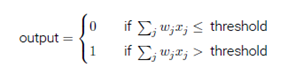




S型神经元
如果对权重(或者偏置)的微小的改动真的能够仅仅引起输出的微小的变化,那我们可以利用这一事实来修改权重和偏置,让我们的网络能够表现得像我们想要的那样。问题在于当我们的网络包含感知器时这不会发生。实际上,网络中单个感知器上一个权重或偏置的微小改动有时会引起那个感知器的输出完全翻转,如0变到1。那样的翻转可能接下来引起其余网络的行为以机器复杂的方式完全改变。这使得逐步修改权重和偏置来让网络接近期望行为变得困难。
我们可以引入一种称为S型神经元的新的人工神经网络来克服这个问题。S型神经元和感知器类似,但是被修改为权重和偏置的微小改动只引起输出的微小变化。这对让神经元网络学习起来是关键的。
好了,让我来描述下S型神经元。我们用描述感知器的相同方式来描述S型神经元:
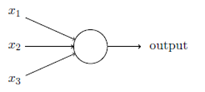
正如一个感知器,S型神经元有多个输入,但是这些输入可以取0和1中的任意值,而不仅仅是0或1。例如, 0.638……是一个S型神经元的有效输入。同样,S型神经元对每个输入有权重,和一个总的偏置,b。但是输出不是0或1.相反,它现在是, 这里被称为S型函数,定义为:
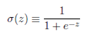
把它们放在一起来更清楚地说明,一个具有输入权重和偏置b的S型神经元的输出是:
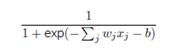
初看上去,S型神经元和感知器由很大的差别。实际上,感知器和S型神经元之间有很多相似的地方。S型神经元和感知器的对比图如下:

感知器和S型神经元之间一个很大的不同是S型神经元不仅仅输出0或1。它可以输出0和1之间的任何实数,所以诸如0.173…和0.689…的值是合理的输出。
由于历史的原因,尽管是由S型神经元而不是感知器构成,这种多层网络有时被称为多层感知器或者MLP。
目前为止,讨论的神经网络,都是以上一层的输入作为下一层的输出。这种网络被称为前馈神经网络。
使用梯度下降算法进行学习
我们希望有一个算法,能让我们找到权重和偏置,以至于网络的输出y(x)能够拟合所有的训练输入x。为了量化我们如何实现这个目标,我们定义一个代价函数:

这里w表示所有的网络中权重的集合,b是所有的偏置,n是训练输入数据的个数,a是表示当输入为x时输出的向量,求和则是在总的训练输入x上进行的。