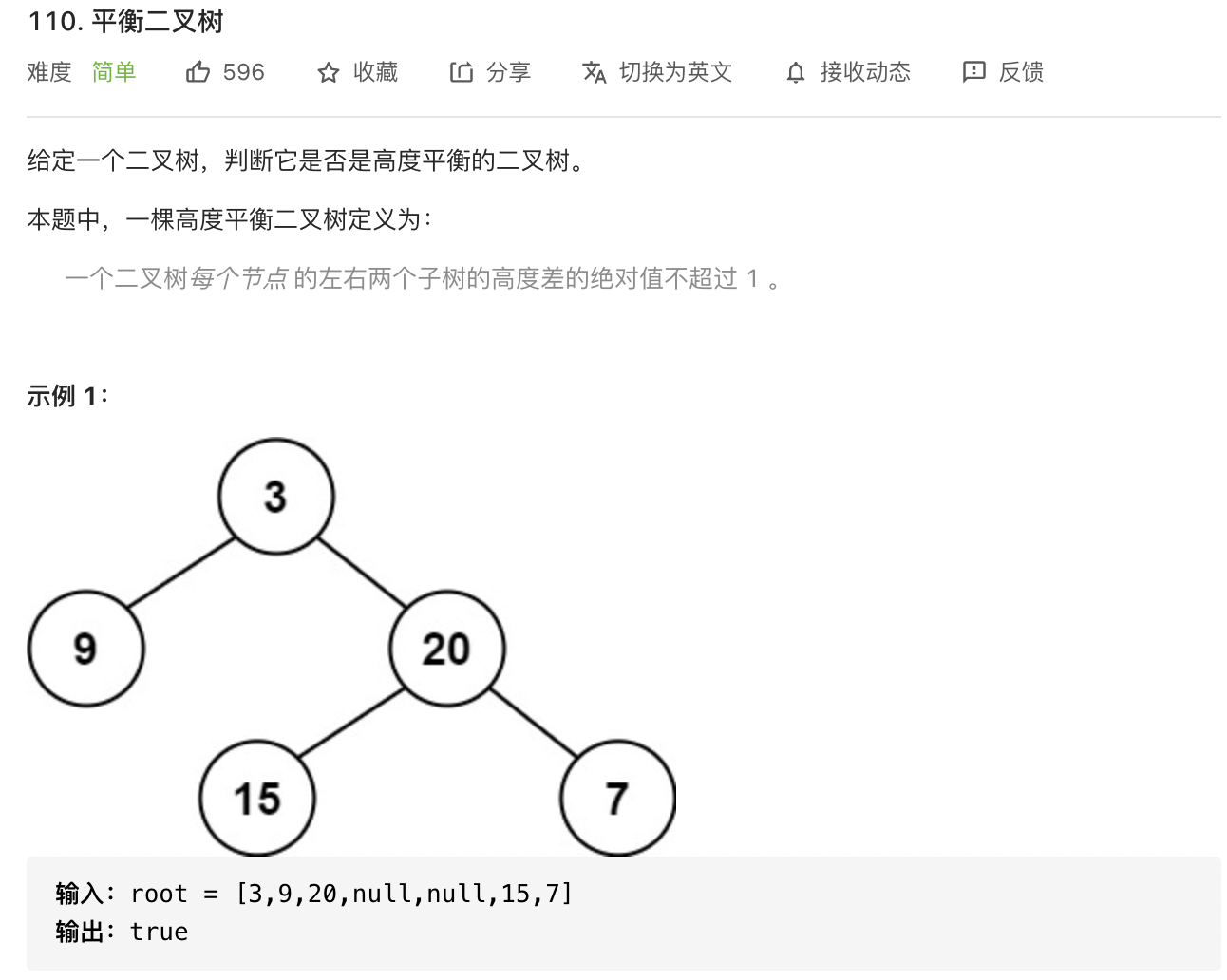
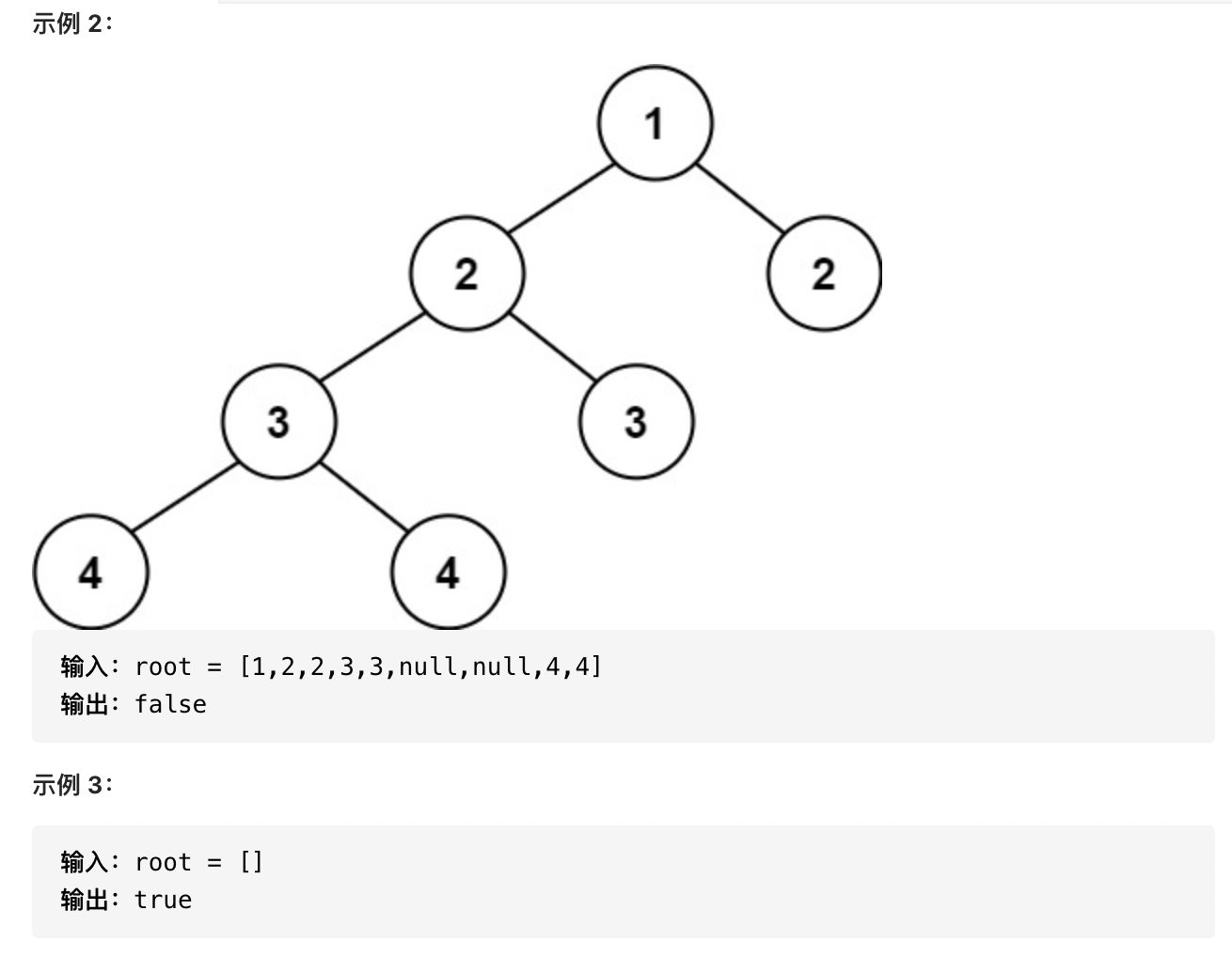
判断一个树是不是平衡二叉树,关键要看其左右子树的树高差是否大于1,如果一直到根节点其左右子树的树高差都不大于1的话,那么就可以认为这是一棵平衡二叉树。
所以这道题本质上是对树的高度的一个变种题,先递归到子节点,然后层层往上遍历,一旦出现某个点左右子树的树高差大于1,那么直接置为false就可以了,而用一个全局变量来保存是否是平衡二叉树的状态,这样最终返回的结果就是是否为平衡二叉树了。
看下代码:
private boolean result = true; public boolean isBalanced1(TreeNode root) { maxDepth(root); return result; } public int maxDepth(TreeNode head) { if (head == null) return 0; int left = maxDepth(head.left); int right = maxDepth(head.right); if(Math.abs(left - right) > 1) result = false; return Math.max(left,right) + 1; }
定义一个类变量result用来传递递归的结果;
整个isBalanced函数里面就是一个递归的函数maxDepth,用于改变result的结果;
再来看下递归函数maxDepth
if (head == null) ---> return 0; 其实是作为递归的出口,就是说如果到了左节点或者是右节点为null的情况下就返回0;
然后找出左节点的树高,找出右节点的树高;如果任意一个节点的左右子节点的高度差大于1的话,那么就将result置为false;
之后继续return本节点的树高:即Math.max(left,right) + 1 就是左右子节点的最大树高,然后+1 向上传递;
但是这个代码有个问题就是在已经发现了不是平衡树的情况下仍然要继续向上递归,一直走到递归的入口根节点处才能够退出递归的过程,这其实是有问题的;
其实一旦某个子节点不是平衡树了之后在往上就没有必要继续判断了,后面的所有判断过程都是多余的,所以其实可以剪枝优化一下:
看下面这段代码:
public boolean isBalanced(TreeNode root) { if (root == null) return true; return getDepth(root) != -1; } public int getDepth(TreeNode head) { if( head == null) return 0; int left = getDepth( head.left ); if(left == -1) return -1; int right = getDepth( head.right ); if (right == -1) return -1; return Math.abs(left - right) > 1 ? -1 : Math.max(left, right) + 1; }
这段代码的好处在于往上递归到任何一个节点的时候,都会进行一次判断,如果说其左右任何子树,返回结果是-1 或者说其判断自身左右子树的高度差结果大于1 ,都会继续往上返回-1,这样
便可以做到一旦出现-1就立马一路返回而不进行任何的判断过程,相比于第一种写法来说,算是一种优化;