二分图
https://oi-wiki.org/graph/bi-graph/
黑白染色,邻点异色
二分图一定无奇环(奇环——边数点数都是奇数)
完全二分图 用kn,m表示(完全图用kn表示)
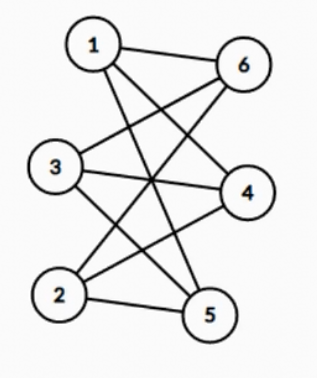
染色
判断二分图
首先任意取出一个顶点进行染色,和该节点相邻的点有三种情况:
1.未染色 那么继续染色此节点(染色为另一种颜色)
2.已染色但和当前节点颜色不同 跳过该点
3.已染色并且和当前节点颜色相同 返回失败(该图不是二分图)
0表示还未访问,1表示在集合A中,2表示在集合B中。
col(color)储存颜色,初始化为0.
vector <int> v[N];
void dfs(int x,int y) {
col[x]=y;
for (int i=0;i<v[x].size();i++) {
if (!col[v[x][i]]) dfs(v[x][i],3-y);
if (col[v[x][i]]==col[x]) FLAG=true;
}
}
for (i=1; i<=n; i++) col[i]=0;
for (i=1; i<=n; i++) if (!col[i]) dfs(i,1);
if (FLAG) cout<<"NO"<<endl;
else cout<<"YES"<<endl;
判断奇环(flag==1奇环)
染色例题
注意,在每个连通块里都要取最小值
#include<iostream>
#include<cstdio>
#include<cstring>
#include<vector>
using namespace std;
#define N 200050
vector< int >g[N];
int n,m,ans1,ans2,ans;
int col[N],dep[N];//1 white 2 black
bool flag,vis[N];
void dfs(int x,int c){
col[x]=c;
if(c==1)ans1++;
else ans2++;
for(int i=0;i<g[x].size();i++){
int y=g[x][i];
if(!col[y])dfs(y,3-c);
else if(col[y]==col[x]) flag=1;
}
}
void check(int x){
for(int i=0;i<g[x].size();i++){
int y=g[x][i];
if(!vis[y])vis[y]=1,dep[y]=dep[x]+1,check(y);
else if((dep[x]-dep[y])%2==0)flag=1;
}
}
int main(){
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++){
vis[i]=1;col[i]=100;
}
for(int i=1,x,y;i<=m;i++){
scanf("%d%d",&x,&y);
g[x].push_back(y);
g[y].push_back(x);
vis[x]=vis[y]=0;
col[x]=col[y]=0;
}
flag=0;
for(int i=1;i<=n;i++)
if(!vis[i])vis[i]=1,check(i);
for(int i=1;i<=n;i++){
ans1=ans2=0;
if(!col[i])dfs(i,1);
ans+=min(ans1,ans2);
}
if(flag)puts("Impossible");
else printf("%d
",ans) ;
return 0;
}
关押罪犯
这道题有一种扩展域并查集的解法,戳这里
题意抽象出来的模型就是:
给定一张无向图,边有边权。
找到最小的权值(k) ,使得只保留权值(>k)的边时,图是一张二分图。
二分答案(细节),二分图染色判定即可
#include<iostream>
#include<cstdio>
#include<cstring>
#include<vector>
#include<algorithm>
#include<utility>
#include<queue>
using namespace std;
#define N 20005
#define M 100005
int n,m,ans=0,cnt;
bool vis[N];
int col[N];
int u[N],v[N],w[N];
int head[M<<1];
struct edge{
int to,nxt,w;
}e[M<<1];
void add(int u,int v,int w){
e[++cnt]=(edge){v,head[u],w};
head[u]=cnt;
}
bool check(int mid){
memset(col,0,sizeof(col));
queue< int >q;
for(int i=1;i<=n;i++){
if(!col[i]){
col[i]=1;q.push(i);
while(q.size()){
int x=q.front();q.pop();
for(int i=head[x];i;i=e[i].nxt){
if(e[i].w>=mid){
int y=e[i].to;
if(!col[y]){
q.push(y);
col[y]=col[x]==1?2:1;
}
else if(col[y]==col[x])return 1;
}
}
}
}
}
return 0;
}
int main(){
scanf("%d%d",&n,&m);
int l=0,r=0;
for(int i=1,u,v,w;i<=m;i++){
scanf("%d%d%d",&u,&v,&w);
r=max(r,w);
add(u,v,w);add(v,u,w);
}
r++;
while(l+1<r){
int mid=(l+r)>>1;
if(check(mid))l=mid;
else r=mid;
}
printf("%d",l);
return 0;
}
CF85E Guard Towers
二分答案mid+二分图——和上一题思路几乎一样
曼哈顿距离 >mid 的点连边,判定是否构成二分图
方案数=2^最终的二分图连通块数目
当然也有并查集的做法戳上题那里
卡卡常
#include <queue>
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
typedef long long LL;
const int N=5005;
const int mod=1e9+7;
inline int read() {
int x=0,f=1;char ch=getchar();
while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();}
while(isdigit(ch)){x=x*10+ch-'0';ch=getchar();}
return f*x;
}
inline void Max(int &x,int y){if(x<y)x=y;}
inline int jue(int x) {return x>0?x:(-x);}
int n,x[N],y[N];
inline int dis(int i,int j) {
return jue(x[j]-x[i])+jue(y[j]-y[i]);
}
int col[N],ans;
bool flag=0;
inline bool dfs(int x,int mid,int c) {
for(int i=1;i<=n;i++)
if(dis(i,x)>mid) {//将距离大于mid的染色
if(col[i]) {
if(col[i]==3-c) continue;
else return 1;
}
col[i]=3-c;
if(dfs(i,mid,3-c)) return 1;
}
return 0;
}
inline bool check(int mid) {
memset(col,0,sizeof(col));
for(int i=1;i<=n;i++)
if(!col[i]) {
col[i]=1;
if(dfs(i,mid,1)) return 0;
}
return 1;
}
int vis[N];
void get(int x,int num) {
queue<int>q;
vis[x]=num;
q.push(x);
while(!q.empty()) {
int y=q.front();q.pop();
for(int i=1;i<=n;i++) {
if(vis[i]||dis(i,y)<=ans) continue;
vis[i]=num;
q.push(i);
}
}
}
LL qpow(LL a,LL b) {
LL ans=1;
while(b) {
if(b&1) ans=ans*a%mod;
a=a*a%mod;
b>>=1;
}
return ans;
}
int main() {
n=read();
for(int i=1;i<=n;i++)
x[i]=read(),y[i]=read();
int l=0,r=10000;
while(l<=r){
int mid=(l+r)>>1;
if(check(mid)) ans=mid,r=mid-1;
else l=mid+1;
}
printf("%d
",ans);
int num=0;
for(int i=1;i<=n;i++)
if(!vis[i])
get(i,++num);
printf("%lld",qpow(2,num));
return 0;
}
匹配
定义见blog
设G=<V, E>为二分图,如果 M⊆E,并且 M 中任意两条边没有公共端点,则成M为G的一个匹配。【匹配的实质是一些边的集合】
下图的红线就是一个匹配

最大匹配: 选取边数尽可能多(边数固定,但不一定唯一)
就是说在这A,B两个集合中不断选择两个存在连线(只有存在连线才能连起来,而且每个点只能匹配一次)的两个点相连,求最多可以有多少条连线即这个二分图的最大匹配数----下图中红色即最大匹配
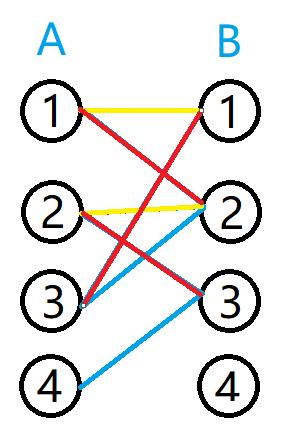
完美匹配: 所有点都在匹配中(每个点恰好属于1条匹配边)完美匹配一定是最大匹配。但并非每个图都存在完美匹配。
交错路: 从非匹配点出发, 依次经过非匹配边、 匹配边、 非匹配边. . .
增广路: 从非匹配点出发, 结束于非匹配点的交错路
而对于一个点来说,判断从它出发能否在另一个集合中找到一个顶点使得整张图的总匹配数增加的过程实际上可以理解为一个找寻增广路的过程
匈牙利算法O(mn)
求二分图的最大匹配
增广路定理: 任意一个有最大匹配的匹配一定存在增广路
初始没有选中的边 寻找增广路 找到增广路则将路径中匹配边和非匹配边对换
找到一条增广路会使最大匹配加一
模板
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
typedef long long ll;
const int N=1005;
const int M=5e4+10;
inline int read() {
int x=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
return f*x;
}
int n,m,e;
int g[N][N];
bool vis[N];
int link[N];
bool find(int x) {
for(int i=1;i<=m;i++) {
if(g[x][i]&&!vis[i]) {
vis[i]=1;
if(!link[i]||find(link[i])) {
link[i]=x;
return 1;
}
}
}
return 0;
}
int ans;
int main() {
n=read();m=read();e=read();
for(int i=1;i<=e;i++) {
int u=read(),v=read();
g[u][v]=1;
}
for(int i=1;i<=n;i++) {
memset(vis,0,sizeof(vis));//这步注意
if(find(i)) ans++;
}
printf("%d",ans);
return 0;
}
数据范围大于1000用链式前向星存图
座位安排
#include<iostream>
#include<cstdio>
#include<cstring>
#include<vector>
#include<algorithm>
#include<utility>
#include<queue>
using namespace std;
#define N 2005
int n,ans=0,cnt;
bool vis[N];
int link[N][2],head[N<<1];
struct edge{
int to,nxt;
}e[N<<2];
void add(int u,int v){
e[++cnt]=(edge){v,head[u]};
head[u]=cnt;
}
bool find(int x){
for(int i=head[x];i;i=e[i].nxt){
int y=e[i].to;
if(!vis[y]){
vis[y]=1;
if(!link[y][0] || find(link[y][0])){
link[y][0]=x;return 1;
}
if(!link[y][1] || find(link[y][1])){
link[y][1]=x;return 1;
}
}
}
return 0;
}
int main(){
scanf("%d",&n);
for(int i=1,x,y;i<=2*n;i++){
scanf("%d%d",&x,&y);
add(i,x);add(i,y);
}
for(int i=1;i<=2*n;i++){
memset(vis,0,sizeof(vis));
if(find(i))ans++;
}
printf("%d",ans);
return 0;
}
飞行员配对方案问题
裸题+输出连边
#include<iostream>
#include<cstdio>
#include<cstring>
#include<vector>
#include<algorithm>
#include<utility>
#include<queue>
using namespace std;
#define N 205
inline int read()
{
int x=0,k=1; char c=getchar();
while(c<'0'||c>'9'){if(c=='-')k=-1;c=getchar();}
while(c>='0'&&c<='9')x=(x<<3)+(x<<1)+(c^48),c=getchar();
return x*k;
}
int g[N][N],link[N];
bool vis[N];
int n,m,x,y,ans;
bool dfs(int x){
for(int i=1;i<=n;i++){
if(g[x][i]&&!vis[i]){
vis[i]=1;
if(!link[i] || dfs(link[i])){
link[i]=x;return 1;
}
}
}
return 0;
}
int main(){
m=read();n=read();
while(1){
x=read();y=read();
if(x==-1&&y==-1)break;
g[y][x]=1;g[x][y]=1;
}
for(int i=1;i<=m;i++){
memset(vis,0,sizeof(vis));
if(dfs(i))ans++;
}
printf("%d
",ans);
for(int i=1;i<=n;i++)
if(link[i])printf("%d %d
",link[i],i);
return 0;
}
其他结论
二分图最小点覆盖:尽可能少的点覆盖所有边。
König定理: 二分图的最小点覆盖在数值上等于最大匹配。
最小边覆盖:尽可能少的边覆盖所有点。
最小边覆盖在数值上等于 点数减转化后的二分图的最大匹配数。
二分图最大独立集
二分图最大独立集在数值上等于最小边覆盖。 (等于点数减最大匹配数)
最小路径覆盖:DAG上用多少条互不相交的路径覆盖所有点
最小路径覆盖在数值上等于 点数减转化后的二分图的最大匹配数。

棋盘模型01要素
01要素见blog
矩阵游戏
n*m的棋盘,把每一行看成一个点,每一列看成一个点,那么每一个格子就是一个行点到一个列点的一条边
行列连二分图,满足题意需有n个黑子不同行且不同列
只需找最大匹配即可
#include <bits/stdc++.h>
using namespace std;
#define maxn 110000
int tot=0,v[maxn],hd[maxn],nxt[maxn];
int link[maxn];
bool vis[maxn];
void add(int a,int b){
nxt[++tot]=hd[a];
v[tot]=b;
hd[a]=tot;
}
bool find(int x){
if(!vis[x]){
vis[x]=1;
for(int i=hd[x];i;i=nxt[i]){
if(!link[v[i]] || find(link[v[i]])){
link[v[i]]=x;
return true;
}
}
return false;
}
}
int main(){
int T;
scanf("%d",&T);
while(T--){
int n;
scanf("%d",&n);
memset(hd,0,sizeof(hd));
memset(link,0,sizeof(link));
tot=0;
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++){
int x;
scanf("%d",&x);
if(x) add(i,j);
}
int ans=0;
for(int i=1;i<=n;i++){
memset(vis,0,sizeof(vis));
if(find(i)) ans++;
}
if(ans==n) printf("Yes
");
else printf("No
");
}
return 0;
}
棋盘覆盖
也是二分图棋盘模型
格子是点,骨牌是边,(i+j)&1为奇数点,否则为偶数点,我们发现肯定是奇数点连偶数点。
找最大匹配
#include <cstdio>
#include <vector>
#include <cstring>
#include <utility>
#include <iostream>
#include <algorithm>
using namespace std;
const int N=505;
inline int read() {
int x=0,f=1;char ch=getchar();
while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();}
while(isdigit(ch)){x=x*10+ch-'0';ch=getchar();}
return f*x;
}
int n,m,tag[N][N];
int hd[N*N],nxt[N*N],to[N*N],tot;
inline void add(int x,int y) {
to[++tot]=y;nxt[tot]=hd[x];hd[x]=tot;
}
int dx[]={0,0,-1,1};
int dy[]={-1,1,0,0};
inline int id(int i,int j){return i*n+j;}
int link[N*N],vis[N*N],num;
bool dfs(int x) {
for(int i=hd[x];i;i=nxt[i]) {
int y=to[i];
if(num!=vis[y]) {
vis[y]=num;
if(!link[y]||dfs(link[y])){
link[y]=x;
return 1;
}
}
}
return 0;
}
int main() {
n=read();m=read();
int x,y;
for(int i=1;i<=m;i++)
tag[read()][read()]=1;
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
if(!tag[i][j]){
if((i+j)&1) {
for(int k=0;k<=3;k++) {
int x=i+dx[k],y=j+dy[k];
if(x>=1&&x<=n&&y>=1&&y<=n&&!tag[x][y])
add(id(i,j),id(x,y));
}
}
}
int ans=0;
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
if((i+j)&1)
num++,ans+=dfs(id(i,j));
cout<<ans<<endl;
return 0;
}
poj2446
最小点覆盖
tag表示洞
#include<cstdio>
#include<cstring>
const int N=2000+5;
using namespace std;
int cnt[N][N],tag[N][N],g[N][N],link[N];
int n,m,x,y,k,ans,cntx;
bool vis[N];
void init(){
ans=0;cntx=0;
memset(link,0,sizeof(link));
memset(cnt,0,sizeof(cnt));
memset(tag,0,sizeof(tag));
memset(g,0,sizeof(g));
}
bool find(int x){
int v;
for(int j=1;j<=cntx;j++){
if((!vis[j]) && g[x][j]){
vis[j]=true;
if((!link[j]) || (find(link[j]))){
link[j]=x;
return true;
}
}
}
return false;
}
int main(){
while(scanf("%d%d%d",&m,&n,&k)==3){
init();
for(int i=1;i<=k;i++){
scanf("%d%d",&y,&x);
tag[x][y]=1;
}
for(int i=1;i<=m;i++)
for(int j=1;j<=n;j++)
if(!tag[i][j])
cnt[i][j]=++cntx;
for(int i=1;i<=m;i++)
for(int j=1;j<=n;j++)
if(!tag[i][j]){
if(j>1&& !tag[i][j-1]) g[cnt[i][j]][cnt[i][j-1]]=1;
if(j<n && !tag[i][j+1]) g[cnt[i][j]][cnt[i][j+1]]=1;
if(i>1&& !tag[i-1][j]) g[cnt[i][j]][cnt[i-1][j]]=1;
if(i<m && !tag[i+1][j]) g[cnt[i][j]][cnt[i+1][j]]=1;
}
for(int i=1;i<=cntx;i++){
memset(vis,false,sizeof(vis));
if(find(i))
ans++;
}
if(ans==cntx) printf("YES
");
else printf("NO
");
}
return 0;
}
例题:
wait 双栈排序
首先考虑只有一个栈的时候如何解决这个问题。
就是对于一对位置 ((i, j))不能存在三个位置 (i < j < k) 存在 (p_k < p_i < p_j),因为$ p_k$ 需要在 (p_i)与 (p_j) 之前出栈,但 (p_i) 又需要在 (p_j) 之前出栈,那么这就会产生矛盾。
我们预处理 (33-39),就可以在 (O(n ^ 2))的时间内判断一对 (i, j)是否可以共存了(40--43判断)
然后对于存在两个栈的情况,我们就需要把 (p)划分成两个序列,使得这两个序列之中的数都互不冲突。
这样的话,我们对于一对不能共存的 (i, j)连边,然后进行二分图染色。如果不可染,那么就是不存在一组合法解。(48--51)
之后我们只需要解决使得最后解字典序最小的限制。
我们染色的时候 BFS 染色,尽量把在前面的放入第一个栈
1 #include<cstdio>
2 #include<cstdlib>
3 #include<iostream>
4 #include<algorithm>
5 #include<stack>
6 #include<cmath>
7 using namespace std;
8 #define maxn 1004
9
10 const int inf=19260817;
11 int n,num;
12 int col[maxn];
13 int t[maxn];
14 int s[maxn];
15 bool f,e[maxn][maxn];
16
17 void paint(int x,int c){
18 col[x]=c;
19 for(int i=1;i<=n;i++){
20 if(e[x][i]){
21 if(col[i]==c) f=false;
22 if(!col[i]) paint(i,3-c);
23 }
24 }
25 }
26
27 int main(){
28 f=1;
29 scanf("%d",&n);
30 for(int i=1;i<=n;i++){
31 scanf("%d",&t[i]);
32 }
33 s[n+1]=inf;
34 for(int i=n;i>=1;i--){
35 s[i]=t[i];
36 if(s[i+1]<s[i]){
37 s[i]=s[i+1];
38 }
39 }
40 for(int i=1;i<=n;i++)
41 for(int j=i+1;j<=n+1;j++)
42 if(t[i]<t[j]&&s[j+1]<t[i])//不合条件
43 e[i][j]=e[j][i]=1;
44 for(int i=1;i<=n;i++){
45 if(!col[i])
46 paint(i,1);
47 }
48 if(f==false){
49 printf("0
");
50 return 0;
51 }
52 stack<int> st1,st2;
53 int cnt=1;
54 for(int i=1;i<=n;i++){
55 if(col[i]==1){
56 st1.push(t[i]);
57 printf("a ");
58 }else{
59 st2.push(t[i]);
60 printf("c ");
61 }
62 while((!st1.empty() && st1.top()==cnt) || (!st2.empty() && st2.top()==cnt)){
63 if(!st1.empty() && st1.top()==cnt){
64 st1.pop();
65 cnt++;
66 printf("b ");
67 }else{
68 st2.pop();
69 cnt++;
70 printf("d ");
71 }
72 }
73 }
74 return 0;
75 }
http://www.51nod.com/Challenge/Problem.html#problemId=1368
问最多——舍弃最少点
舍弃白棋 或者 舍弃白棋周围空格
白棋向周围空格连边
跑最小点覆盖
http://www.51nod.com/Challenge/Problem.html#problemId=2929
带权匹配 KM算法
