数据结构与算法各种基础知识的代码

快速排序：

def quick_sort(array, left, right):
    """
    :type array: list
    :type left: int
    :type right: int
    :return:type list
    """
    if left < right:
        i = partition(array, left, right)
        quick_sort(array, left, i)
        quick_sort(array, i+1, right)
    return array


def partition(a, left, right):
    middle = (left + right) / 2  # the middle element is the pivot
    pivot = a[middle]
    a[middle], a[right-1] = a[right-1], a[middle]  # swap middle element with the last element
    i = left - 1
    for j in range(left, right):
        if a[j] > pivot:
            i += 1
            a[j], a[i] = a[i], a[j]
    a[i+1], a[right-1] = a[right-1], a[i+1]
    return i+1

ar = [2, 4, 5, 6, 7, 8, 9, 234, 123, 324, 52, 423, 42, 4, 23, 4, 5, 12, 5, 15, 1, 5, 51, 142]
print quick_sort(ar, 0, len(ar))

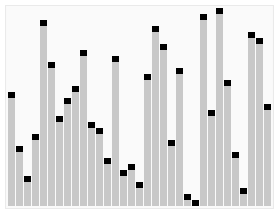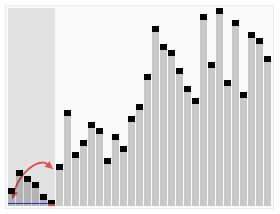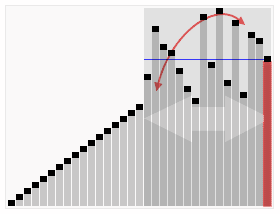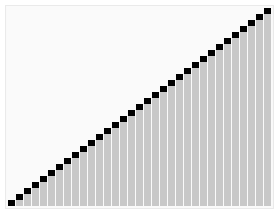
采用in_place方法，选取数组中间元素作为基准值，首先将基准值换到数组最后，然后遍历数组，有一个指针i记录分割位置，遍历结束i指在大于基准值和小于等于基准值的分界点，最后将基准值与i+1元素换位从而完成基准值的位置确定，然后递归解决问题。

树 前，中，后序遍历：

 

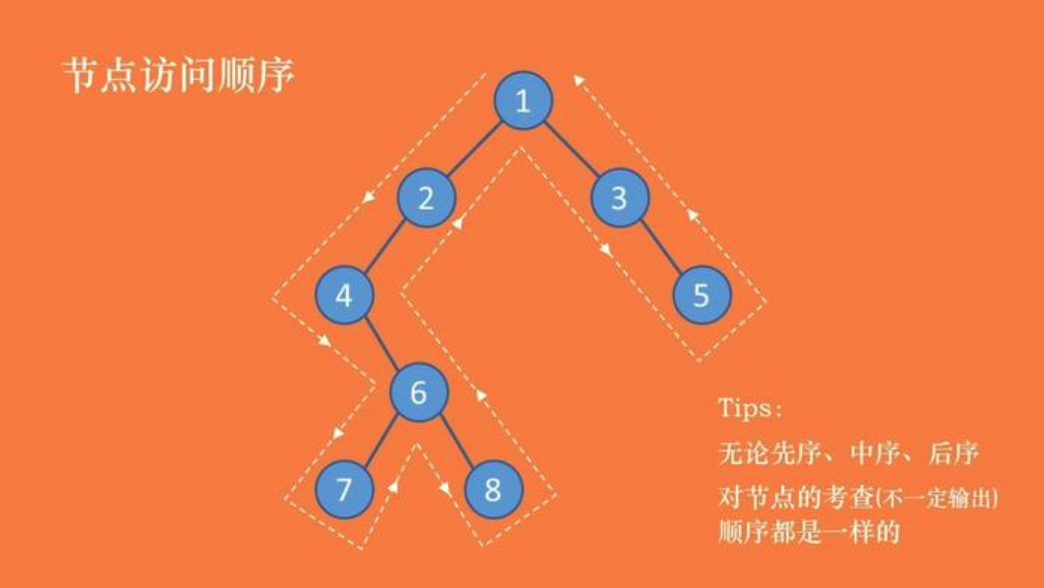
图片选自 https://www.jianshu.com/p/456af5480cee

上图顺序很好理解，就是从左到右终极描边。

前序：就按终极描边的顺序来。  所以结果是：12467835

中序：按终极描边来，只要有左节点就跳过，没有就输出。 所有结果是：47682135

后序：按终极描边来，有子节点就跳过，没有就输出。 所以结果是：78642531

堆排序：

#!/usr/bin/env python
#-*-coding:utf-8-*-

def heap_sort(lst):
    def sift_down(start, end):
        """最大堆调整"""
        root = start
        while True:
            child = 2 * root + 1
            if child > end:
                break
            if child + 1 <= end and lst[child] < lst[child + 1]:
                child += 1
            if lst[root] < lst[child]:
                lst[root], lst[child] = lst[child], lst[root]
                root = child
            else:
                break

    # 创建最大堆
    for start in xrange((len(lst) - 2) // 2, -1, -1):
        sift_down(start, len(lst) - 1)

    # 堆排序
    for end in xrange(len(lst) - 1, 0, -1):
        lst[0], lst[end] = lst[end], lst[0]
        sift_down(0, end - 1)
    return lst
            
def main():
    l = [9,2,1,7,6,8,5,3,4]
    heap_sort(l)

if __name__ == "__main__":
    main()

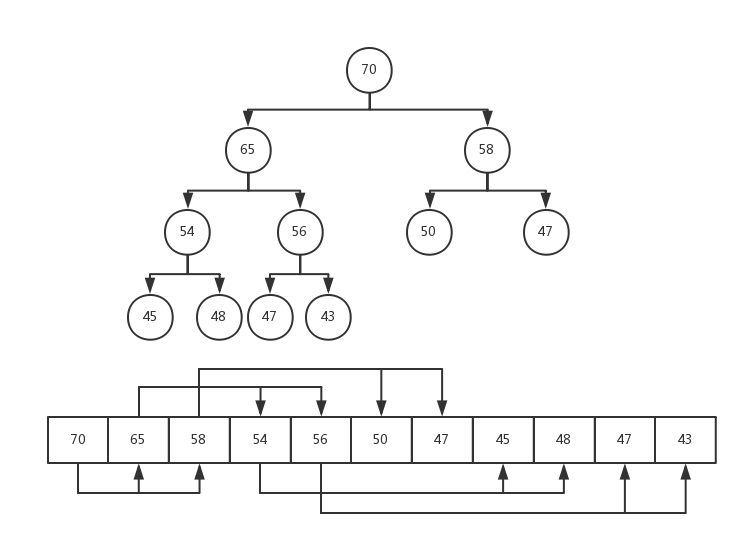
上图解释了heap_sort函数中第一个循环的索引计算。下图为堆调整的过程，代码主要思路是首先先将数组按照最大堆的规则进行排序，而排序是从最后一个节点的父节点开始，依次到达root节点。之后将符合最大堆规则的数组的第一个元素移除，代码中表现为将第一个元素与最后一个元素交换位置，然后将小一号的数组进行最大堆的调整，然后继续将第一个最后一个换位置，如此循环。最后数组为从小到大依次排序的。

 

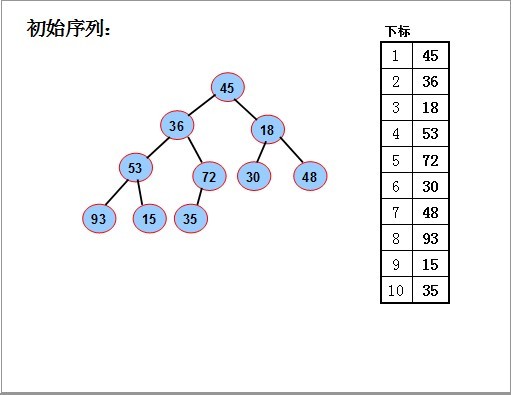
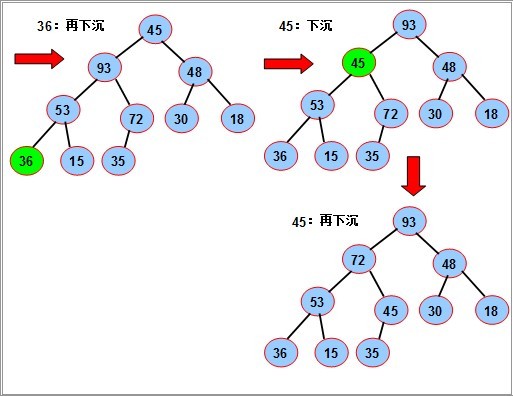
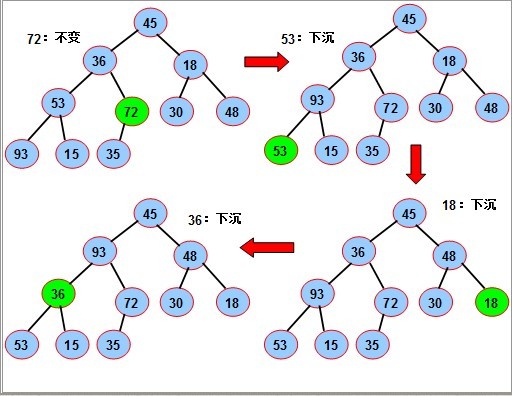
图片来自 http://128kj.iteye.com/blog/1728555 结合代码和图片可以很好理解

关于二叉搜索树：https://www.61mon.com/index.php/archives/191/ 详细问题及解法