边权递增最短路
题目链接
思路就是题解里的思路,主要说一下错误的原因:
- 1.将边权相等的边都处理好后也是要取(min)的,虽然是可以更新才放进去的,但还是要取(min),举个例子
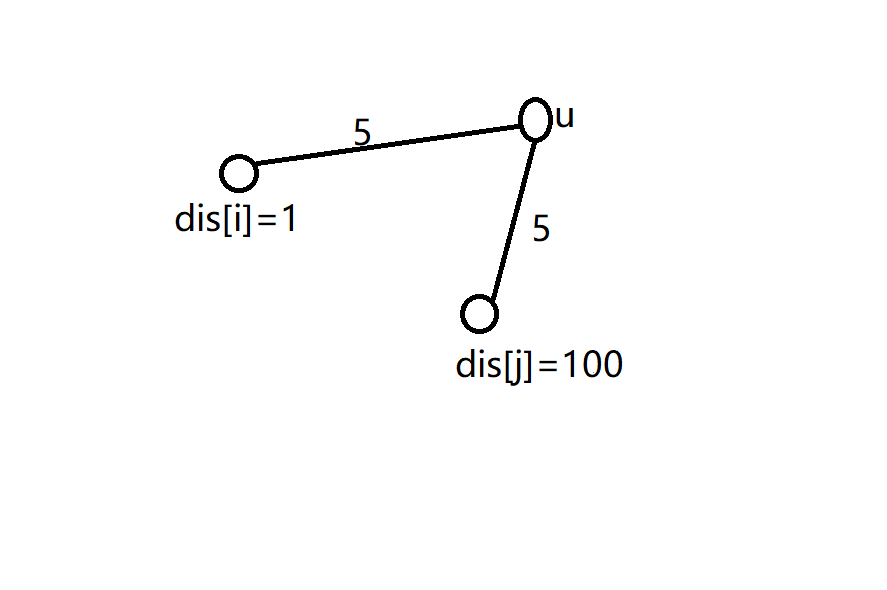
当用(i\,j)更新(u)的时候直接赋值就会出错。
- 2.当(while)循环结束时,队列中可能还有元素,要把他们也加进去。
还有就是写(while)的话还是一次一次的来吧,如果(while)里再写一个(while)的话,很可能会炸边界。(参见第一次提交)
((while)的话还是少用吧,边界炸好多次了。
终极版代码:
#include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdio>
#include<queue>
#define MP make_pair
#define fi first
#define se second
#define u e[i].from
#define v e[i].node
#define LL long long
using namespace std;
const LL N = 100005;
const LL inf = 4557430888798830399;
typedef pair<LL,LL> pll;
LL n,m,tot,dis[N],T,num;
struct edge{
LL node,data,from;
}e[N<<1];
/*struct node{
LL val,id;
}q[N];*/
queue<pll> q;
void add(LL x,LL y,LL z)
{
e[++tot].node=y;
e[tot].from=x;
e[tot].data=z;
}
bool cmp(const edge &x,const edge &y)
{ return x.data<y.data; }
void solve()
{
memset(dis,0x3f,sizeof(dis));
scanf("%lld%lld",&n,&m);
dis[1]=0; tot=0; num=0;
LL x,y,z,last=0;
for(LL i=1;i<=m;i++)
{
scanf("%lld%lld%lld",&x,&y,&z);
add(x,y,z);
}
sort(e+1,e+tot+1,cmp);
/* for(LL i=1;i<=tot;i++)
{
if(e[i].data!=e[i-1].data)
{
while(!q.empty())
{
dis[q.front().se]=min(q.front().fi,dis[q.front().se]);
q.pop();
}
}
if(dis[u]>dis[v]+e[i].data)
q.push(MP(dis[v]+e[i].data,u));
if(dis[v]>dis[u]+e[i].data)
q.push(MP(dis[u]+e[i].data,v));
}
while(!q.empty())
dis[q.front().se]=min(q.front().fi,dis[q.front().se]),q.pop();*/
LL i=1;
while(i<=tot)
{
if(e[i].data==e[i-1].data)
{
if(dis[u]>dis[v]+e[i].data)
q.push(MP(dis[v]+e[i].data,u));
if(dis[v]>dis[u]+e[i].data)
q.push(MP(dis[u]+e[i].data,v));
}
else
{
while(!q.empty())
{
LL j=q.front().se,k=q.front().fi;
dis[j]=min(k,dis[j]); q.pop();
}
if(dis[u]>dis[v]+e[i].data)
q.push(MP(dis[v]+e[i].data,u));
if(dis[v]>dis[u]+e[i].data)
q.push(MP(dis[u]+e[i].data,v));
}
++i;
/*bool flag=0;
while(e[i+1].data==e[i].data)
{
flag=1;
if(dis[u]>dis[v]+e[i].data)
q.push(MP(dis[v]+e[i].data,u));
if(dis[v]>dis[u]+e[i].data)
q.push(MP(dis[u]+e[i].data,v));
++i;
}
if(flag)
{
if(dis[u]>dis[v]+e[i].data)
q.push(MP(dis[v]+e[i].data,u));
if(dis[v]>dis[u]+e[i].data)
q.push(MP(dis[u]+e[i].data,v));
++i;
}
while(!q.empty())
{
LL j=q.front().se,k=q.front().fi;
dis[j]=min(k,dis[j]); q.pop();
}
if(!flag)
{
if(dis[u]>dis[v]+e[i].data)
dis[u]=dis[v]+e[i].data;
if(dis[v]>dis[u]+e[i].data);
dis[v]=dis[u]+e[i].data;
++i;
}*/
}
while(!q.empty())
{
LL j=q.front().se,k=q.front().fi;
dis[j]=min(k,dis[j]); q.pop();
}
if(dis[n]==inf) printf("No answer
");
else printf("%lld
",dis[n]);
return ;
}
int main()
{
scanf("%lld",&T);
while(T--) solve();
return 0;
}
某个最短路题(1)
题目链接
首先,课件上的做法是假的。
真的:
先建好所有公路和铁路,跑一遍最短路,维护一下使得最短路经过的边最多。这样的话当最短路相等但经过的边数较多时也是要进队的。不进的话可能会错吧,没试过。
统计答案:
方法一:对于每条铁路,如果他能到达的点的最短路经过的的边数为1,铁路的长度等于最短路的长度,并且只走公路到达这个点的最短路大于铁路的长度,那么这条铁路是必须的。
!!!但是,假如说这条必须的铁路有多条一模一样的,我们只留一条就行。也就是说这些铁路中只有一条是必须的,其他的又变成不必须的了。(错点)
方法二((zxy)):对于除1号点以外的所有点,如果到它的最短路经过的边数为1,且最短路长度等于到它的最短的铁路的长度,并且不等于到它的直达的公路的长度,那么有一条铁路是必须的。这样就避免了多条一模一样的铁路的情况。
代码:
#include<iostream>
#include<cstring>
#include<cstdio>
#include<queue>
#define MP make_pair
#define fi first
#define se second
#define LL long long
using namespace std;
const int N = 4e5+5;
typedef pair<LL,int> pll;
LL dis[N];
bool book[N];
int n,m,k,head[N],tot,ans,num[N],dism[N],len[N];
priority_queue<pll,vector<pll>,greater<pll> > q;
struct edge{
int node,next,data;
}e[N<<1];
struct Node{
int len,to;
}a[N];
void add(int x,int y,int z)
{
e[++tot].node=y;
e[tot].next=head[x];
head[x]=tot;
e[tot].data=z;
}
void dij()
{
memset(dis,0x3f,sizeof(dis));
dis[1]=0;
q.push(MP(0,1));
while(!q.empty())
{
int u=q.top().se;
if(dis[u]!=q.top().fi)
{
q.pop(); continue;
}
q.pop();
for(int i=head[u];i;i=e[i].next)
{
int v=e[i].node;
if(dis[v]>dis[u]+(LL)e[i].data)
{
dis[v]=dis[u]+(LL)e[i].data;
num[v]=num[u]+1;
q.push(MP(dis[v],v));
}
else if(dis[v]==dis[u]+(LL)e[i].data)
{
if(num[u]+1>num[v])
{
num[v]=num[u]+1;
q.push(MP(dis[v],v));
}
}
}
}
}
int main()
{
memset(dism,0x3f,sizeof(dism));
scanf("%d%d%d",&n,&m,&k);
int x,y,z;
for(int i=1;i<=m;i++)
{
scanf("%d%d%d",&x,&y,&z);
add(x,y,z); add(y,x,z);
if(x>y) swap(x,y);
if(x==1) dism[y]=min(dism[y],z);
}
for(int i=1;i<=k;i++)
{
scanf("%d%d",&a[i].to,&a[i].len);
add(1,a[i].to,a[i].len); add(a[i].to,1,a[i].len);
if(len[a[i].to]!=0) len[a[i].to]=min(len[a[i].to],a[i].len);
else len[a[i].to]=a[i].len;
}
dij(); ans=k;
/* for(int i=2;i<=n;i++)
{
if(num[i]==1)
{
if(dis[i]==len[i]&&dism[i]!=dis[i])
--ans;
}
}*/
for(int i=1;i<=k;i++)
{
if(num[a[i].to]==1&&dis[a[i].to]==a[i].len)
{
if(dism[a[i].to]!=dis[a[i].to]&&!book[a[i].to])
--ans,book[a[i].to]=1;
}
}
printf("%d
",ans);
return 0;
}
例题X
题目地址
课件上的例题。
注意初值(dis[i][i]=0),还有边的数组要开够。
巧妙地将枚举边变成了枚举点。

#include<iostream>
#include<cstring>
#include<cstdio>
using namespace std;
const int N = 505;
int n,m;
int ans[N][N],dis[N][N],num[N][N];
struct edge{
int u,v,len;
}e[N*N];
int main()
{
scanf("%d%d",&n,&m);
int x,y,z;
memset(dis,0x3f,sizeof(dis));
for(int i=1;i<=m;i++)
{
scanf("%d%d%d",&x,&y,&z);
e[i].u=x; e[i].v=y; e[i].len=z;
dis[x][y]=min(dis[x][y],z);
dis[y][x]=min(dis[y][x],z);
}
for(int i=1;i<=n;i++) dis[i][i]=0;
for(int k=1;k<=n;k++)
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
dis[i][j]=min(dis[i][j],dis[i][k]+dis[k][j]);
for(int s=1;s<=n;s++)
{
for(int i=1;i<=m;i++)
{
if(dis[s][e[i].u]==dis[s][e[i].v]+e[i].len) ++num[s][e[i].u];
if(dis[s][e[i].v]==dis[s][e[i].u]+e[i].len) ++num[s][e[i].v];
}
for(int t=1;t<=n;t++)
for(int k=1;k<=n;k++)
if(dis[s][t]==dis[s][k]+dis[k][t]) ans[s][t]+=num[s][k];
}
for(int i=1;i<=n;i++)
for(int j=i+1;j<=n;j++)
printf("%d ",ans[i][j]);
return 0;
}
某个最短路题(2)
题目要求(minlimits_{j=1}^{n}{2*d(i,j)+a_j}),
这个形式不好看,我们转化一下:
求(minlimits_{j=1}^{n}{2*d(i,j)+d(0,j)})
这样就变成了(minlimits_{i=1}^{n}d(0,i))
然后建一个超级源,求超级源到所有点的最短路就行了。
#include<iostream>
#include<cstring>
#include<cstdio>
#include<queue>
#define MP make_pair
#define fi first
#define se second
#define LL long long
using namespace std;
const LL N = 400005;
LL n,m,a[N],head[N],tot,dis[N];
struct edge{
LL node,next,data;
}e[N<<2];
typedef pair<LL,LL> pll;
priority_queue<pll,vector<pll>,greater<pll> > q;
void add(LL x,LL y,LL z)
{
e[++tot].node=y;
e[tot].next=head[x];
head[x]=tot;
e[tot].data=z;
}
void dij()
{
memset(dis,0x3f,sizeof(dis));
dis[0]=0;
q.push(MP(0,0));
while(!q.empty())
{
LL u=q.top().se;
if(dis[u]!=q.top().fi)
{ q.pop(); continue; }
q.pop();
for(LL i=head[u];i;i=e[i].next)
{
LL v=e[i].node;
if(dis[v]>dis[u]+e[i].data)
{
dis[v]=dis[u]+e[i].data;
q.push(MP(dis[v],v));
}
}
}
}
int main()
{
scanf("%lld%lld",&n,&m);
LL x,y,z;
for(LL i=1;i<=m;i++)
{
scanf("%lld%lld%lld",&x,&y,&z);
add(x,y,2*z); add(y,x,2*z);
}
for(LL i=1;i<=n;i++)
{
scanf("%lld",&z);
add(0,i,z); //add(i,0,z);
}
dij();
for(LL i=1;i<=n;i++)
printf("%lld ",dis[i]);
return 0;
}
另一道最小生成树题
大佬的博客
借鉴过来:
一张图上的最小生成树的性质:
- 对于任意权值的边,所有最小生成树中这个权值的边的数量是一定的
- 对于任意正确加边方案,加完小于某权值的所有边后图的连通性是一样的
所以对于不同权值的边,它们是否同时出现在最小生成树中是互不影响的。所以对于每组询问,我们只需要判断相同权值的边是否能同时出现在最小生成树中即可。
对于每组询问,我们分开考虑,每次只考虑一种权值的边。对于所有权值为(w)的边,我们需要把原图中所有权值小于(w)的边加进去(并查集),然后依次加询问中权值为(w)的边,看是否有环。
加原图中的边时我们不能暴力加边。
来了,大佬神奇的预处理:
在询问之前,预处理出每种权值的边在加完小于该权值的边时,它的两个端点分别属于哪个集合。
然后相当于把原图中所有代表元为(x)的点,都看作(x)。只要两个代表元联通,那么这两个集合也都联通了。
这样的话,我们以加完小于该权值的所有边的时候的代表元为端点,这样就相当于合并了之前的集合。
...
然后还学到了点处理相同集合的方法:
预处理时:
(i)从1开始,到(m)结束。
每次先求一下一条边的代表元,然后如果有和这条边的权值相等的边的话把这些边的代表元都求出来。这一步用(do...\,while)实现。然后把这些边一次性加上。这是一次循环。然后下一次循环枚举到的边就可以求代表元了。
询问时:
先加一条边,判断加的这条边是否会构成环。然后将权值与这条边相等的边都加上,每次加边时都要判断是否构成环,如果构成环,直接(break)就行。
错点来了:
如果加边的时候遇到了环,当前加边的(while)直接(break)就行。但是,这是你已经加了一些边了,整个的循环不能直接(break)。必须把原来加过的边都撤销掉,才能停止
#include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdio>
#include<vector>
using namespace std;
const int N = 1000005;
int n,m,k,fa[N],q;
struct edge{
int x,y,val,id;
int tx,ty;
bool operator < (const edge a)const {
return val < a.val;
}
}e[N];
bool cmp(const edge &a,const edge &b)
{ return a.val<b.val; }
bool cmp1(const edge &a,const edge &b)
{ return a.id<b.id; }
int find(int x)
{
if(x==fa[x]) return x;
fa[x]=find(fa[x]);
return fa[x];
}
void merge(int x,int y)
{ fa[find(x)]=find(y); }
int read()
{
char c=getchar();
int ans=0,w=1;
while((c>'9'||c<'0')&&c!='-') c=getchar();
if(c=='-') { w=-1; c=getchar(); }
while(c>='0'&&c<='9')
{ ans=ans*10+c-'0'; c=getchar(); }
return ans*w;
}
int main()
{
n=read(); m=read();
for(int i=1;i<=n;i++) fa[i]=i;
for(int i=1;i<=m;i++)
{
e[i].x=read(); e[i].y=read();
e[i].val=read(); e[i].id=i;
}
sort(e+1,e+m+1);
e[0].val=-1;
for(int i=1;i<=m;)
{
int last=i;
do
{
e[last].tx=find(e[last].x);
e[last].ty=find(e[last].y);
++last;
}while(last<=m&&e[last].val==e[last-1].val);
while(i<last)
{
while(find(e[i].x)==find(e[i].y)&&i<last) ++i;
if(i<last) merge(e[i].x,e[i].y);
// merge(e[i].x,e[i].y);
// i++;
}
/* if(e[i].val!=e[i-1].val)
{
for(int j=last;j<i;j++)
e[j].tx=find(e[j].x),
e[j].ty=find(e[j].y);
last=i;
}
merge(e[i].x,e[i].y);*/
}
sort(e+1,e+m+1,cmp1);
for(int i=1;i<=n;i++) fa[i]=i;
q=read();
while(q--)
{
k=read();
vector<edge> v;
for(int i=1;i<=k;i++)
{
int x=read();
v.push_back({e[x].tx,e[x].ty,e[x].val});
}
sort(v.begin(),v.end());
int sz=v.size()-1;
bool flag=0;
for(int i=0;i<=sz;)
{
if(v[i].x==v[i].y) { flag=1; break; }
merge(v[i].x,v[i].y);
int j=i+1;
while(j<=sz&&v[j].val==v[i].val)
{
if(find(v[j].x)==find(v[j].y))
{ flag=1; break; }
merge(v[j].x,v[j].y); ++j;
}
while(i<j)
{
fa[v[i].x]=v[i].x;
fa[v[i].y]=v[i].y;
++i;
}
if(flag) break;
}
if(flag) printf("NO
");
else printf("YES
");
}
return 0;
}