树的重量

题目传送门

太巧妙了。。。
推荐大佬的题解

当(n=2)时，答案就是(dis[1][2])
那么答案大于2时呢？

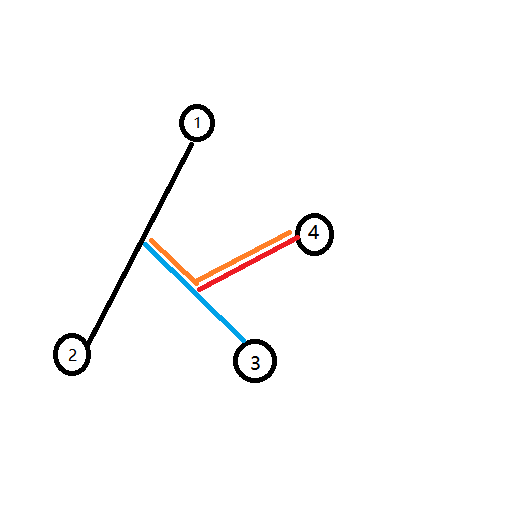
考虑3号点，因为1，和2号点的路径已经统计到答案里去了，3号点对答案产生的贡献只有蓝色部分的路径长度。那怎么求呢？考虑弗洛伊德求最短路的方法，借助中间点更新（这里不太一样啊(hhh)）。3号点一定在1号和2号节点路径的分支上，那么(dis[1][3]+dis[2][3]-dis[1][2])就等于蓝色部分路径长度的两倍。
接下来考虑4号点，由于我们现在不知道它是从于1号点相连的那个点的分支连出来的，所以需要枚举一下。假如枚举出一个点不是我们所要求的点。如图，4号点是从1号点到3号点的路径中连出来的分支（这里说的分支是指最小的一个，因为其他的一定已经加进答案里去了）。如果我们当前枚举到了2号点，那么求出来的答案会是橙色路径的长度，但我们实际要求的其实是红色路径的长度。考虑这两条路径的区别，发现橙色的路径比红色的路径长！所以我们枚举的时候取最小的一个就行了。
至此，此题完美解决。

#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
const int N = 35;
int n,ans,len,dis[N][N];
int main()
{
	scanf("%d",&n);
	while(n!=0)
	{
		ans=0;
		for(int i=1;i<=n;i++)
		 for(int j=i+1;j<=n;j++)
		  scanf("%d",&dis[i][j]);
		ans=dis[1][2];
		for(int i=3;i<=n;i++)
		{
			len=1054612165;
			for(int j=2;j<i;j++)
			{
				len=min(len,(dis[1][i]+dis[j][i]-dis[1][j])>>1);
			}
			ans+=len;
		}
		printf("%d
",ans);
		scanf("%d",&n);
	}
	return 0;
}