验证码识别之二值化

前言

二值化顾名思义就是将数变成两种值，一般非0即1。而在验证码处理中，如果直接使用灰度图，那么每个像素的值会在0-255，这样肯定会增加计算时间，而二值化后每个像素的值只是0和1。

在前面的简单验证码识别中，我的二值化代码是这样写的：a = (a > 180) * 255，至于这里为什么不乘1而乘255，因为我要显示图片看看效果。如果只是用于算法识别的话，乘1会更好。但是，这里的180也就是二值化的阈值是如何得到的，开始是通过一个一个试然后看效果哪个好就选哪个，因为我们一般只识别某个网站的验证码，这样只要测试几次得到结果后便可用于这个网站其他的验证码。

这样测试有点浪费时间，虽然是一次性的，但是你手动测出的验证码不一定是最合适的。所以我们需要算法去自动计算出验证码的阈值，算法有很多，这里我们使用迭代法和最大类间方差法，通过这两个算法计算出来的阈值基本差不多。

迭代法

1. 求出图像中的最小灰度值和最大灰度值，分别记为Gmin和Gmax,则阈值初值T0=(Gmin+Gmax)/2;

2. 根据阈值T0将图像分割成前景和背景两部分，求出两部分的平均灰度值m1和m2,平均灰度值=总灰度值/像素个数

3. 求出新阈值T1=(m1+m2)/2

4. 如果T0=T1，则结束，否则将T1的值赋予T0，从第2步重新计算。

算法实现如下：

import numpy as np
from PIL import Image

def iteration(img_path):
	img = Image.open(img_path).convert('L')
	a = np.array(img)
    a = a.ravel()
    k = int((int(a.max()) + int(a.min()))/2) # 即初始阈值T0
    m = -1
    while k != m:
    	# C1和C2为前景和背景的像素
        C1 = a[a >= k]   
        C2 = a[a < k]
        k = m
        m1 = np.sum(C1)/len(C1) if len(C1) else 0
        m2 = np.sum(C2)/len(C2) if len(C2) else 0
        m = int((m1 + m2)/2)
    return k 

最大类间方差法(OTSU)

原理参考：https://blog.csdn.net/weixin_40647819/article/details/90179953

这里我直接复制一遍：

存在阈值T将图像所有像素分为前景和背景，则这两类像素各自的均值就为m1、m2，图像全局均值为mG。同时像素被分为前景和背景的概率分别为p1、p2。因此就有：
p1*m1+p2*m2=mG 和 p1+p2=1 则类间方差表达式为：

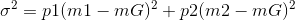
使得上式值最大时的阈值T就是最佳的阈值。

算法实现如下：

import numpy as np
from PIL import Image

def otsu(img_path):
	img = Image.open(img_path).convert('L')
	a = np.array(img)
    a = a.ravel()
    L = []
    for k in range(0, 256):
        C1 = a[a >= k]
        C2 = a[a < k]
        if not(len(C1) and  len(C2)):
            L.append(0)
            continue
        m1 = np.sum(C1)/len(C1)
        m2 = np.sum(C2)/len(C2)
        p1 = len(C1)/len(a)
        p2 = len(C2)/len(a)
        x = p1 * p2 * (m1 - m2) * (m1 - m2)
        L.append(x)
    return L.index(max(L))

看一下效果：
原图

迭代法

最大类间方差法

最后，我正在学习一些机器学习的算法，对于一些我需要记录的内容我都会分享到博客和微信公众号(python成长路)，欢迎关注。平时的话一般分享一些爬虫或者Python的内容。