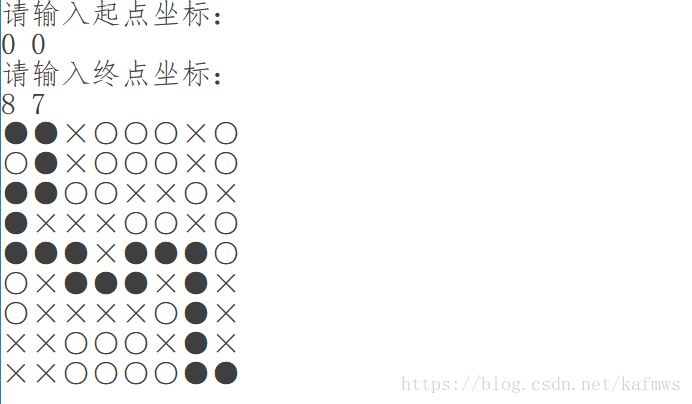栈：栈及表达式求值与迷宫问题的简单应用

栈

栈是一种进出受限的线性表。即仅可在一端进出数据，于是具有FILO（first in last out 先进后出）这种特点。
适合于各种需要回退到上一状态的应用场景。并且通过对进出规则的进一步控制，将优先级转化为出现位置的先后顺序上。
ADT Stack{
　　数据对象：同一数据类型的若干数据的集合
　　结构关系：线性关系
　　基本运算：
　　int initStack(Stack **stack)　　//初始化一个空栈
　　int isEmpty(Stack *stack)　　//判断栈是否为空
　　int isFull(Stack *stack)　　//判断栈是否已满
　　int getTop(Stack *stack, DataType *e)　　//得到栈顶元素存储在变量 *e中
　　int pop(Stack *stack, DataType *e)　　//栈顶元素出栈存储在 *e变量中
　　int push(Stack *stack, DataType data)　　//变量data入栈
}ADT Stack

---

栈的基本运算的实现

int initStack(Stack **stack) {
	*stack = (Stack *)malloc(sizeof(Stack));
	(*stack)->top = -1;
	if (*stack)
		return 1;
	return 0;
}

int isEmpty(Stack *stack) {
	return stack->top == -1;
}

int isFull(Stack *stack) {
	return stack->top == SIZE;
}

int getTop(Stack *stack, double *e) {
	if (!isEmpty(stack)) {
		*e = stack->data[stack->top];
		return 1;
	}
	return 0;
}

int pop(Stack *stack, double *e) {
	if (!isEmpty(stack)) {
		*e = stack->data[stack->top--];
		return 1;
	}
	return 0;
}

int push(Stack *stack, double data) {
	if (!isFull(stack)) {
		stack->top++;
		stack->data[stack->top] = data;
		return 1;
	}
	return 0;
}

---

表达式求值

表达式求值主要有两种思路
1.中缀表达式转后缀表达式再进行计算 仅使用一个栈
2.使用一个操作数栈，一个运算符栈，边处理表达式边计算

根据语言特点，C语言采用第二种方法比较合适

存储结构的选择：在链栈、顺序栈中选择顺序栈

• 首先要分隔输入的操作数与运算符
• 操作数与运算符按规则进出栈并进行运算
• 从栈底取出结果

分隔操作数与运算符

int process(char res[][21]) {//分隔操作数与操作符
	char str[21];
	char c;
	int i = 0, j = 0;
	while ((c = getchar()) != '
') {
		if (isDigit(c)) {//c != '+'&&c != '-'&&c != '*'&&c != '/'&&c != '('&&c != ')'
			str[j++] = c;
		}
		else {
			if (j != 0) {
				str[j] = 0;
				strcpy(res[i++], str);
				j = 0;
			}
			res[i][0] = c;
			res[i++][1] = 0;
		}
	}
	str[j] = 0;
	strcpy(res[i++], str);
	return i;//返回元素个数
}

进出栈规则

初始化两个栈，一个存放运算符，一个放操作数
读入表达式分隔操作数与运算符后，按顺序处理表达式，是操作数直接进栈，运算符则按照如下规则处理

用judge函数判断运算符优先级
规则如下
①左括号直接进栈
②加减优先级相同，乘除优先级相同且高于加减，乘方优先级最高
③若栈空则当前运算符直接入栈，否则与栈顶运算符比较
　　１．当前运算符优先级高则入栈
　　２．栈顶运算符优先级高则弹出它，并从操作符栈弹出两个数进行运算（注意后弹出的数在运算符左侧），运算结果入操作数栈，返回③
　　３．遇到右括号，栈顶运算符依次出栈按2的规则运算，直到栈顶运算符为左括号，且将左括号出栈（注意右括号不做任何处理即舍弃）
④待表达式处理完毕，若操作符栈中仅留存一个元素则计算无误，该元素即为表达式值

//传入当前运算符与栈顶运算符，按优先级得到返回值，比较返回值
int judge(char c) {//min值为1
	int flag = 0;
	switch (c){
		case 0:flag = 0; break;
		case '(': flag = 0; break;
		case '+': flag = 1; break;
		case '-': flag = 1; break;
		case '*': flag = 2; break;
		case '/': flag = 2; break;
		case '^': flag = 3; break;
	}
	return flag;
}

核心流程

int main() {
	char res[SIZE][21];
	printf("请输入计算式：
");
	int size = process(res);//size  数据个数
	Stack *num, *operator;
	if (!initStack(&num) || !initStack(&operator)) { printf("初始化出错！"); return -1; }
	int i, top, now;
	for (i = 0; i < size; i++) {
		if (isDigit(res[i][0])) {//操作数
			push(num, atof(res[i]));
		}
		else if (res[i][0] == '(') {
			push(operator,res[i][0]);
		}
		else {//运算符
			if (res[i][0] != ')') {//  非 )
				double tem = 0;
				now = judge(res[i][0]);//计算当前运算符优先级
				do {
					getTop(operator,&tem);//取得栈顶运算符
					top = judge((int)tem);//计算栈顶运算符优先级
					if (now > top)
						push(operator,res[i][0]);
					else {//弹栈运算      **运算结果入栈
						push(num, caculate(num, operator));
					}
				} while (now <= top);
			}
			else {//  当前运算符为  )
				double tem;
				while (getTop(operator,&tem) && ((int)tem != '(')) {//此时栈不可能为空
					push(num, caculate(num, operator));
				}
				pop(operator,&tem);//弹出  (
			}
		}
	}
	while (!isEmpty(operator)) {
		push(num, caculate(num, operator));
	}
	if (num->top != 0)
		printf("计算出错！
");
	double result;
	getTop(num, &result);
	printf("%g", result);
	return 0;
}

其中计算过程caculate函数为

double caculate(Stack *num, Stack *operator) {//进行一次弹栈运算  返回结果
	char c;
	double a, b, re, t;
	pop(operator, &t);//弹出一个运算符
	pop(num, &b);
	pop(num, &a);//弹出两个操作数
	c = (int)t;
	switch (c){
		case '+':re = a + b; break;
		case '-':re = a - b; break;
		case '*':re = a * b; break;
		case '/':re = a / b; break;
		case '^':re = pow(a, b); break;
	}
	return re;
}

为了方便这里用了double类型来存储所有数据

---

迷宫问题

问题描述：输入一个矩阵表示迷宫地图，比如0表示通路，1表示墙壁。告知起点与终点，寻找一条通路。

问题分析：用栈的角度来想的话，这是一个典型的栈的问题，因为一条路走不通，当然要走到上一个路口选另外一边试试。这就是回溯。栈可以保存每个路口你的选择状态，当某种选择不合适时，退回到上一状态，试试另一条路。可以回退到上一状态，是栈重要的特点。以此类推。

存储结构：将矩阵映射为二维数组。以下代码中从左至右为Y方向递增，从上到下以X为方向递增。从（0,0）开始。

从上到下依次为：
地图的行和列
地图矩阵的定义
标记数组的定义 标记走过的路防止转圈圈
试探方向的定义

int n, m;
int map[MAX][MAX];
int book[MAX][MAX] = { 0 };
int steps[4][2] = { {0,1}, {1,0}, {0,-1},{-1,0} };//  →  ↓  ←  ↑

坐标数据类型定义

typedef struct dataElement {
	int x;
	int y;
	int step;//当前试探到的步数step; 0,1,2,3 // 代表四个方向
}Coord;

算法的主要过程

int process(Coord begin, Coord end) {
	int flag = 1;
	push(stack, begin);//设置起点
	book[begin.x][begin.y] = 1;
	Coord *top = (Coord *)malloc(sizeof(Coord));
	*top= begin;//栈顶坐标初始化
	Coord tem = { 0, 0 ,0 };
	while (top->x != end.x||top->y != end.y) {
		if (flag)//可走 说明这是一个新的路口  从第一个方向开始尝试
			top->step = 0;
		else
			top->step++;//回溯后从下一方向继续尝试
		do {
			tem = *top;
			tem.x += steps[top->step][X];
			tem.y += steps[top->step][Y];
			if (0 <= tem.x&&tem.x < n && 0 <= tem.y&&tem.y < m && 
				map[tem.x][tem.y] == 0&& book[tem.x][tem.y] ==0){
				flag = 1;//可行    //分别判断是否在地图内，是否可走，是否走过
			}
			else {
				flag = 0;
				top->step++;
			}
		} while (top->step <= 3 && !flag);//不可行且有余地时继续寻找
		if (flag) {//可行
			push(stack, tem);
			book[tem.x][tem.y] = 1;//标记
		}
		else { //此处无解
			pop(stack, &tem);
			book[tem.x][tem.y] = 0;//去除标记
			if (isEmpty(stack))//无解
				return 0;
		}
		getTop(stack, &top);
	}
	return 1;
}

结果的简单展现

标记及打印路径

void bookTrace() {//标记
	for (int i = 0; i <= stack->top; i++) {
		map[stack->data[i].x][stack->data[i].y] = 9;
	}
}

void print() {
	int i, j;
	for (i = 0; i < n; i++) {
		for (j = 0; j < m; j++) {
			switch (map[i][j]){
			case 0:printf("○"); break;
			case 1:printf("×"); break;
			case 9:printf("●"); break;
			default:printf("DATA ERROR");exit(0);break;
			}
		}
		printf("
");
	}
}

效果

2018/10/11