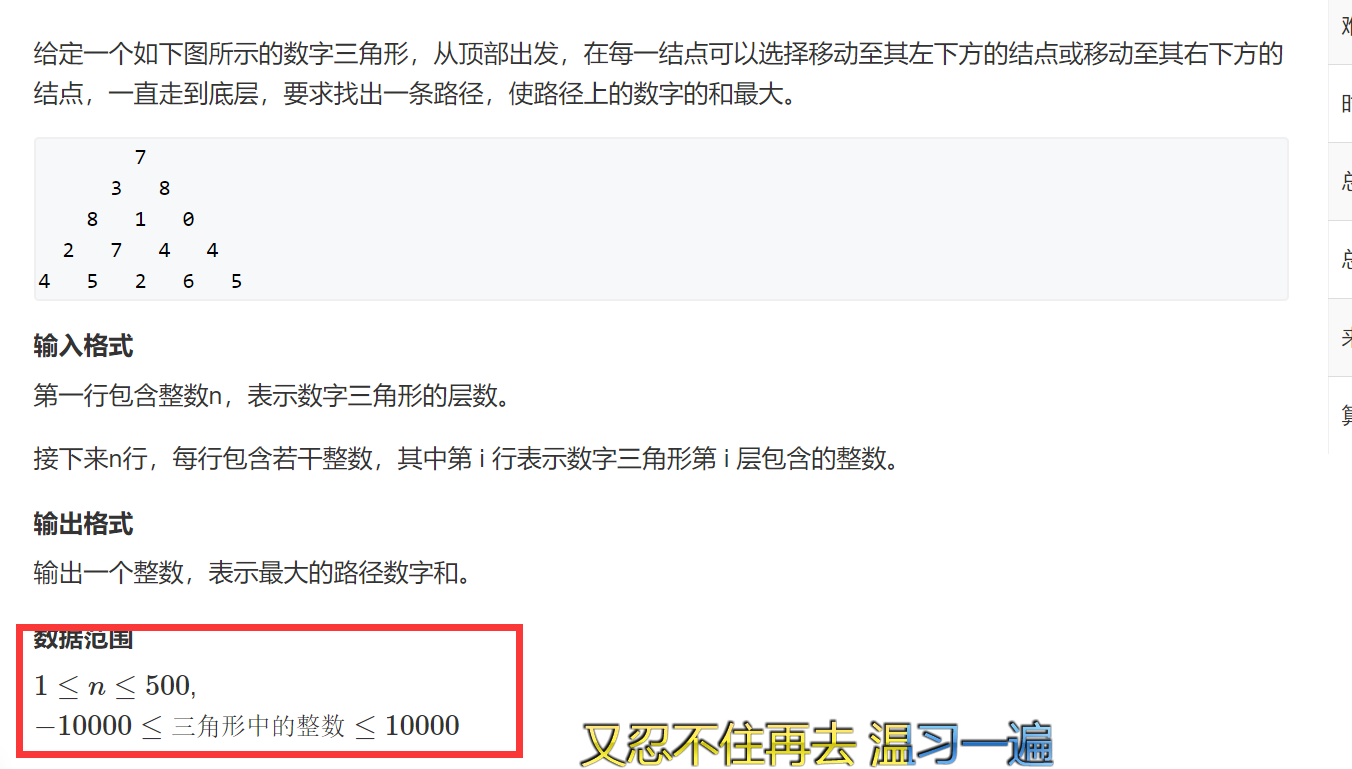
注意点:1、其实就是讲所有走每一步的时候求大致值就好,然后这个值又会对下面进行影响,就像自己思考问题一样
2、然后就是需要注意一下边界问题,因为我们这边求最大值,所以需要对边界进行初始化
#include <iostream>
#include <cstring>
#include <string>
#include <cmath>
#include <cstdio>
#include <stdio.h>
#include <cstdlib>
#include <algorithm>
#include <vector>
#include <set>
#include <map>
#include <queue>
#include <iomanip>
#define pub(n) push_back(n)
#define pob(n) pop_back(n)
#define sf(n) scanf("%d",&n)
#define pf(n) printf("%d
",n)
#define slf(n) scanf("lld",&n)
#define plf(n) printf("lld
",&n)
#define rep(i,a,b) for(int i = a; i <= b ; i ++ )
#define pre(i,a,b) for(int i = a ; i >= b ; i --)
#define ll long long
#define PII pair<int,int>
#define inf 0x3f3f3f3f3f3f3fll
#define ull unsigned long long
#define ios ios::sync_with_stdio(false),cin.tie(0)
using namespace std;
const int N = 510,mod=1e9+7;
int n;
int a[N][N];
int f[N][N];
int main()
{
ios;
sf(n);
rep(i,1,n)
{
rep(j,1,i)
{
sf(a[i][j]);
}
}
rep(i,0,n)
{
rep(j,0,i+1)
{
f[i][j]=-inf;
}
}
f[1][1]=a[1][1];
rep(i,2,n)
{
rep(j,1,i)
{
f[i][j]=max(f[i-1][j-1]+a[i][j],f[i-1][j]+a[i][j]); // select down or right
}
}
int cnt=-inf;
rep(i,1,n)
{
cnt=max(cnt,f[n][i]);
}
pf(cnt);
return 0;
}
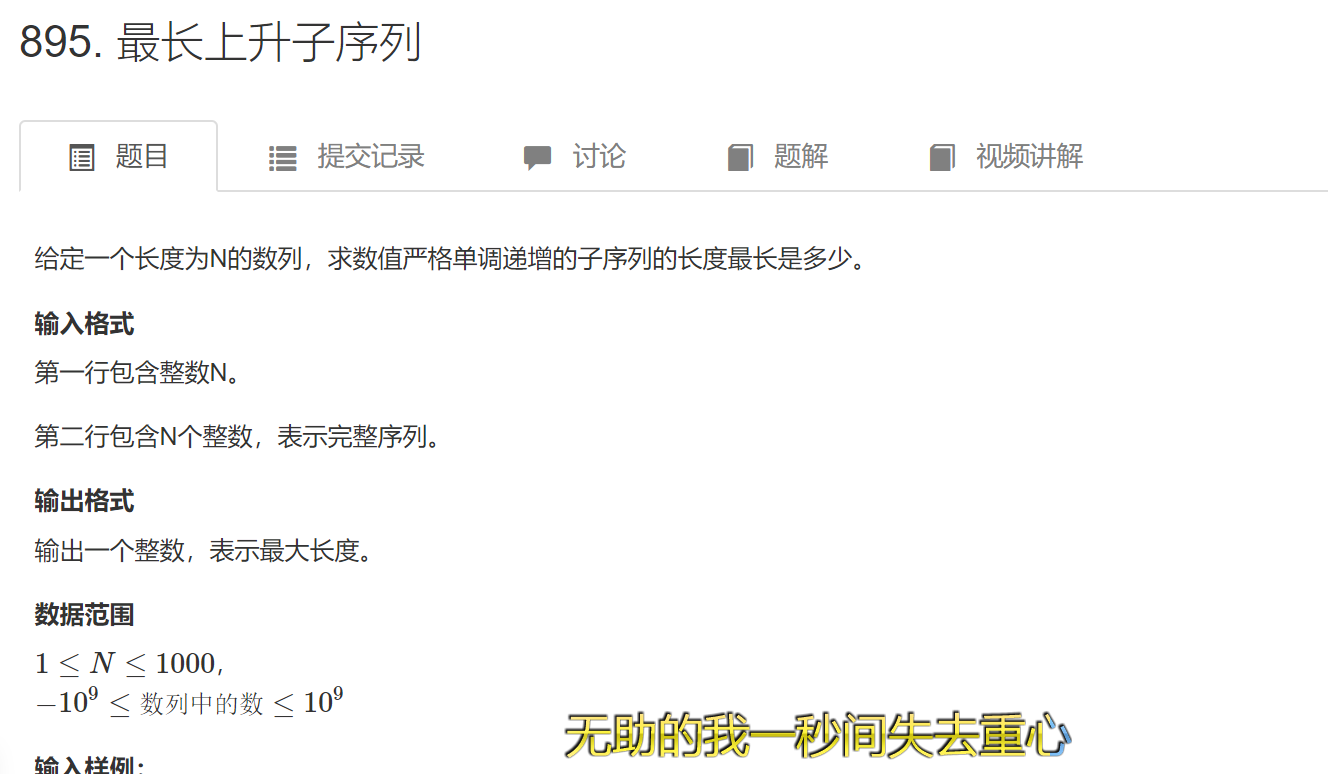
最长上升子序列理解:1、有一说一,样板题,很快就容易,就是当前这个值可以由前面哪里转过来然后max最大长度就行,++就好
#include <iostream>
#include <cstring>
#include <string>
#include <cmath>
#include <cstdio>
#include <stdio.h>
#include <cstdlib>
#include <algorithm>
#include <vector>
#include <set>
#include <map>
#include <queue>
#include <iomanip>
#define pub(n) push_back(n)
#define pob(n) pop_back(n)
#define sf(n) scanf("%d",&n)
#define pf(n) printf("%d
",n)
#define slf(n) scanf("lld",&n)
#define plf(n) printf("lld
",&n)
#define rep(i,a,b) for(int i = a; i <= b ; i ++ )
#define pre(i,a,b) for(int i = a ; i >= b ; i --)
#define ll long long
#define PII pair<int,int>
#define inf 0x3f3f3f3f3f3f3fll
#define ull unsigned long long
#define ios ios::sync_with_stdio(false),cin.tie(0)
using namespace std;
const int N = 1110,mod=1e9+7;
int n;
int a[N];
int f[N];
int main()
{
ios;
sf(n);
rep(i,1,n) sf(a[i]);
rep(i,1,n)
{
f[i]=1;
rep(j,1,i-1)
{
if(a[i]>a[j])
{
f[i]=max(f[i],f[j]+1);
}
}
}
int cnt=-1;// the end index of the max f[i]
rep(i,1,n)
{
cnt=max(cnt,f[i]);
}
pf(cnt);
return 0;
}
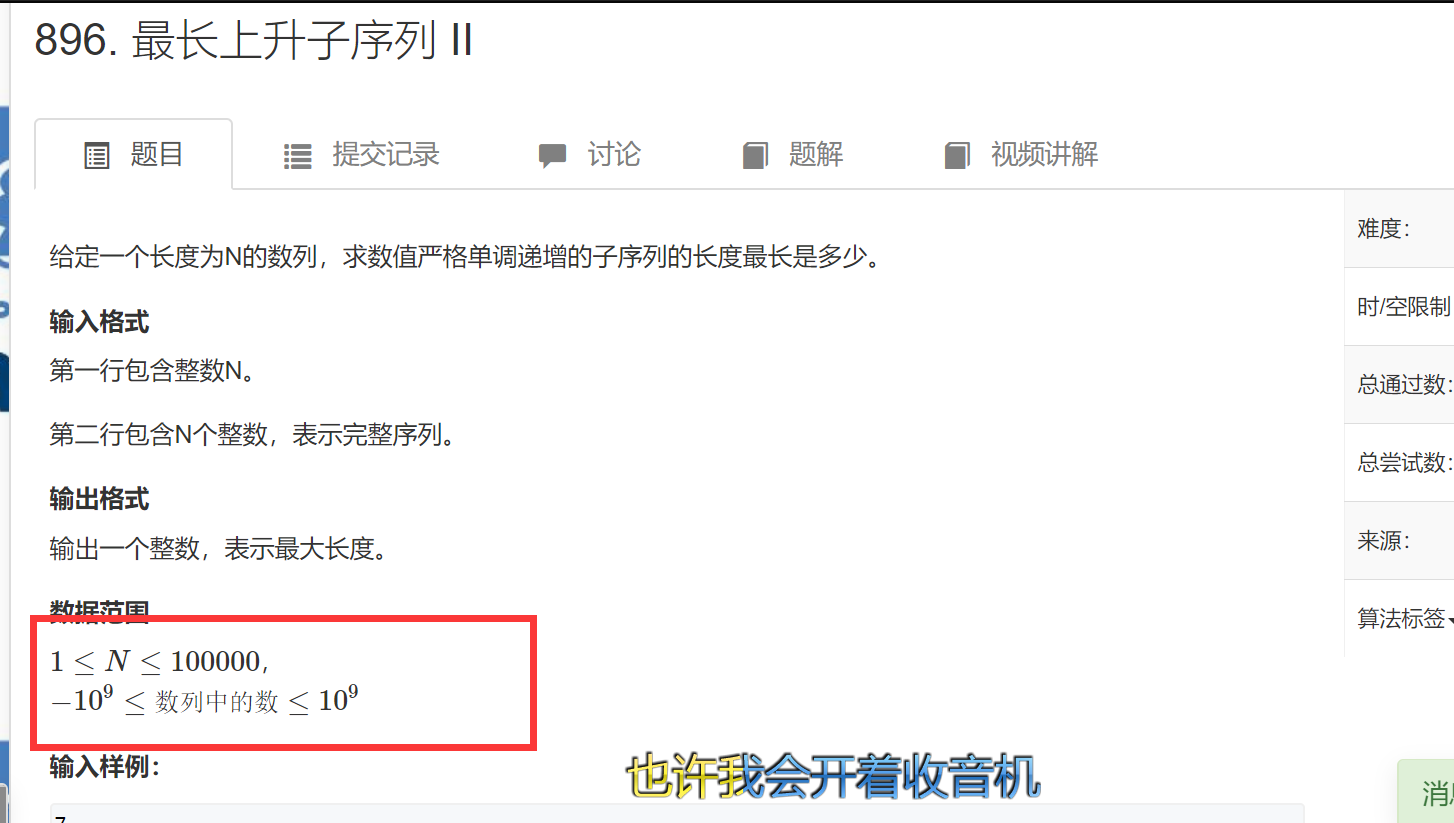
最长上升子序列二思考:1、数据量增大的下我们是无法两重循环的,所以得优化,
2、不难发现没有优化的时候我们是需要枚举出我们是从哪里转过来,然后继续求max
3、如果我们要是能够知道_i_前面的数字的最小值的话,岂不是直接查找当前这个值就好了,不需再进行枚举了
4、所以,这里f[]数组的含义发生了改变,存的是前面i个数最长上升子序列结尾的最小值
#include <iostream>
#include <cstring>
#include <string>
#include <cmath>
#include <cstdio>
#include <stdio.h>
#include <cstdlib>
#include <algorithm>
#include <vector>
#include <set>
#include <map>
#include <queue>
#include <iomanip>
#define pub(n) push_back(n)
#define pob(n) pop_back(n)
#define sf(n) scanf("%d",&n)
#define pf(n) printf("%d
",n)
#define slf(n) scanf("lld",&n)
#define plf(n) printf("lld
",&n)
#define rep(i,a,b) for(int i = a; i <= b ; i ++ )
#define pre(i,a,b) for(int i = a ; i >= b ; i --)
#define ll long long
#define PII pair<int,int>
#define inf 0x3f3f3f3f3f3f3fll
#define ull unsigned long long
#define ios ios::sync_with_stdio(false),cin.tie(0)
using namespace std;
const int N = 2e6+10,mod=1e9+7;
int n;
int a[N];
int f[N];
int main()
{
ios;
sf(n);
rep(i,0,n-1) sf(a[i]);
int len=0; //当前最大的长度
f[0]=-2e9; // after we need to get the min length of adding a[]
rep(i,0,n-1)
{
int l=0,r=len;
while(l<r)
{
int mid =(l+r+1) >> 1;
if(a[i]>f[mid]) l=mid;
else r=mid-1;
}
len=max(len,r+1);
f[r+1]=a[i];
}
pf(len);
return 0;
}
之后就是还有一个最长公共子序列,感觉trie算法更好一点,就不写了
