4月25日课堂随笔

一、进制转换

     十进制 有10个基数：0，1，2，3，4，5，6，7，8，9

     二进制 有2个基数：0，1

     八进制 有8个基数：0，1，2，3，4，5，6，7

     十六进制 有16个基数：0--9，A，B，C，D，E，F（A=10，B=11，C=12，D=13，E=14，F=15）

二、十进制与其他进制之间的转换

  （一）十进制与二进制

      1、十进制转二进制

           十进制数除以2，除商取余，从后至前反向写出，即为二进制数

       例：36除以2得出的商依次为：18   9   4   2   1

               余数依次为：0   0   1   0   0   1

               从右至左依次为：1   0   0   1   0   0

               所以二进制数为：100100

     2、二进制转十进制

          计算公式：a×2º+b×2¹+c×2²+......=...

          其中a代表二进制数中的右边第一位数，b代表右边第二位数，c代表右边地三位数，以此类推。

      例：二进制数1011001转换为十进制数为89

               1×2⁰+0×2¹+0×2²+1×2³+1×2⁴+0×2⁵+1×2⁶

             =1+8+16+64

             =89

  （二）十进制与八进制

      1、十进制转八进制

          十进制数除以8，除商取余，从后至前反向写出，即为八进制数

         *计算方法类同“十进制转二进制”

     2、八进制转十进制

          计算公式：a×8º+b×8¹+c×8²+......=...

          其中a代表二进制数中的右边第一位数，b代表右边第二位数，c代表右边地三位数，以此类推。

      例：八进制数2137转换为十进制数为1119

           7×8⁰+3×8¹+1×8²+2×8³

         =7+24+64+1024

         =1119

   （三）十进制与十六进制

       1、十进制转十六进制

           十进制数除以16，除商取余，从后至前反向写出，即为十六进制数

           *计算方法类同“十进制转二进制”

           0--9，A，B，C，D，E，F（A=10，B=11，C=12，D=13，E=14，F=15）

      2、十六进制转十进制

          计算方法类同二进制、八进制

三、其他进制间的转换

   （一）二进制转八进制

           2的3次方等于8，所以从右至左每三位数为一组，每组单独转换出来，即为八进制

       例：1101111011

            1            101                   111                    011

         1×2⁰     1×2²+1×2⁰      1×2²+1×2¹+1×2⁰      1×2¹+1×2⁰

                 1              5                      7                       3

         所以八进制数为：1573

   （二）八进制转二进制

       例：1                   5                                   7                             3

          1×2⁰        1×2²+1×2⁰        1×2²+1×2¹+1×2⁰       1×2¹+1×2⁰

            1              101                     111                     011

       （1=2⁰      5=4+1=2² + 2⁰     7=4+2+1=2²+2¹+2⁰     3=2+1=2¹+2⁰）

   （三）二进制转十六进制

           2的4次方等于16，所以从右至左每四位数为一组，每组单独转换出来，即为十六进制

      例：  1001                     0111                                 0111                    1001

        1×2³+1×2⁰     1×2²+1×2¹+1×2⁰      1×2²+1×2¹+1×2⁰    1×2³+1×2⁰

                         9                    7                         7                         9

          所以十六进制数为：9779

   （四）十六进制转二进制

       例：  1001                          0111                               0111                   1001

          1×2³+1×2⁰     1×2²+1×2¹+1×2⁰      1×2²+1×2¹+1×2⁰    1×2³+1×2⁰

                       9                        7                             7                    9

          所以二进制数为：1001011101111001

四、各进制之间的关系图

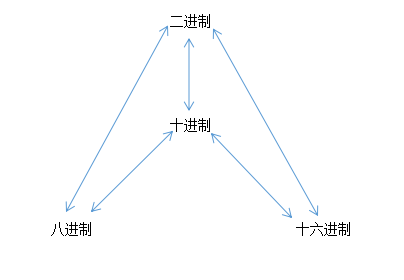
*八进制与十六进制不可直接进行转换，只能通过二进制或者十进制