一、题目:
一个有正有负的整数数组里,其中连续的一个或多个整数构成的整数组,有一个和,求最大子数组,要求,时间复杂度为O(n)
二、设计思路
整体思路:
首先,随机生成任意个(num个)整数(正数,负数),放到数组中。
其次,遍历数组,若遇负数,舍弃((前面的结果)放到另个数组中进行保存),若遇正数开始相加。
(举例: 2 -2 4 3 -7 5 9)
(首先2,保留2,看到-2,舍弃-2,从4开始,3为正,所以4+3保留,因遇-7为负,分别保留7和-7,从5开始,遇到9,加起来,和为14,保留14,;所有保留的数值都放在一个数组内,进行比较,取最大值——最后答案为14)
(文字表示的不是很清楚,此处用数组进行表示,若a[N]为初始数组,m[N*N]为保留数组,则:a[0]=2,a[1]=-2,a[2]=4,a[3]=3,a[4]=-7,a[5]=5,a[6]=9
m[0]=2,m[1]=-2,m[2]=7,m[3]=-7,m[4]=14(保留那些负数的原因:可能全为负))
输入:
无
输出:
输出n,数组里的数是哪些(这个是便于检查自己的程序是否有错)。
输出结果。
三、说明:
- 为了自己验证程序没有错误,只是利用种子,并非真正产生了随机数
- 正数负数使用随机数,可避免巧合(弊端:可能产生全正全负的情况)
四、源程序代码:
//最大子数组的和(相邻)
//20143066毛雯雯,2016.4.5
include
define N 100
include
using namespace std;
void main()
{
int num;
num = rand()%100+1;//随机数的个数
cout<<"产生一个有"<<num <<"个数的数组"<<endl;
int a[N];
int i;
int k;
for(i=0;i<num;i++)
{
k = rand()%2;
if(k==1)
{
a[i] = rand()%100+1;
}
if(k==0)
{
a[i] = 0 - (rand()%100+1);
}
}
cout<< "产生的数组为: " <<endl;
for(i=0;i<num;i++)
{
cout<<a[i]<<" ";
}
cout << endl;
int m[N*N];
int j = 0;
for(i=0;i<N*N;i++)
{
m[i]=0;
}
for(i=0;i<num;i++)
{
if(a[i]>0)
{
m[j]=a[i]+m[j];
}
else
{
j++;
m[j]=a[i];
}
}
int result=m[0];
for(i=0;i<j;i++)
{
cout << m[i] << " ";
if(m[i]>result)
{
result = m[i];
}
}
cout << endl;
cout << "最大子数组的和为:" << result;
}
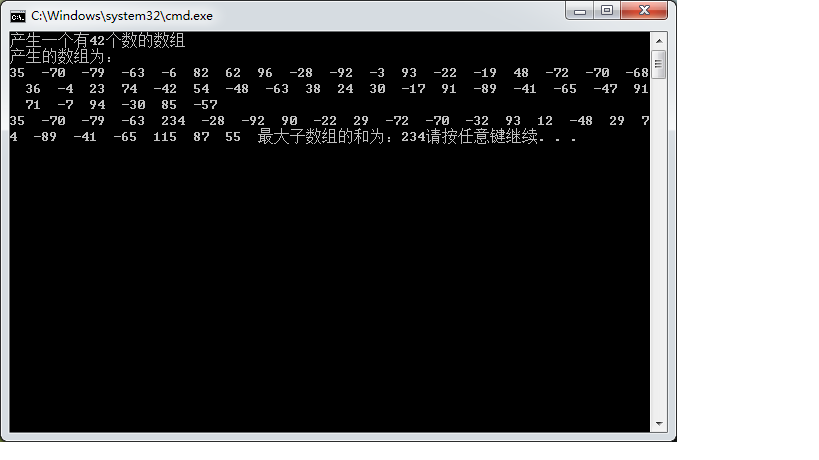
五、运行结果截图:
六、另外的解决方案:
把所以子数组都求出来(不符合复杂度的要求)
七、出现的问题:
- 理解错误,认为是前m个的和>前m+1个的和就可以进行保留
- 忘记对m[]数组进行赋初始值
- 程序中j++的语句为止错误
- 对m[]数组进行找最大值时,将问题复杂化,写成排序
八、总结:
第一次思路错误,没有及时的重新思考,一直在改之前的代码,直到自己意识到这个问题,已经浪费了很多时间。