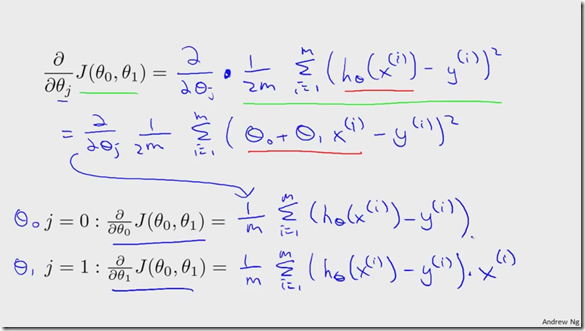一：回归模型介绍
从理论上讲，回归模型即用已知的数据变量来预测另外一个数据变量，已知的数据属性称为输入或者已有特征，想要预测的数据称为输出或者目标变量。
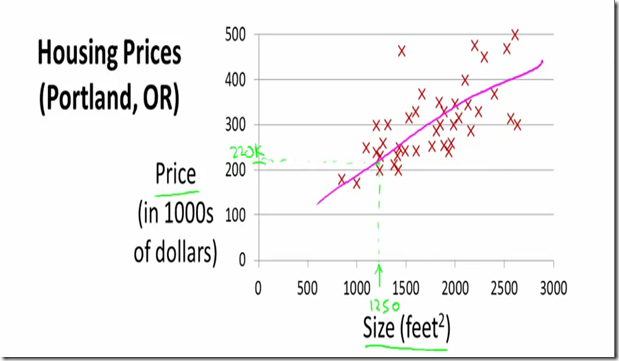
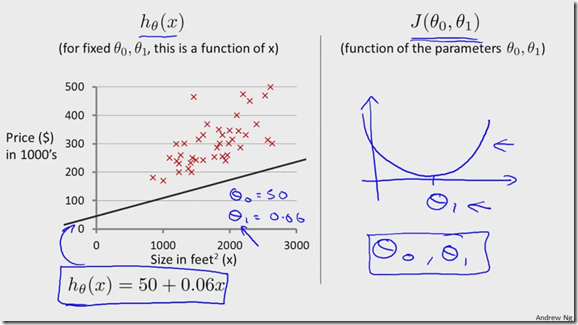
下图是一个例子：
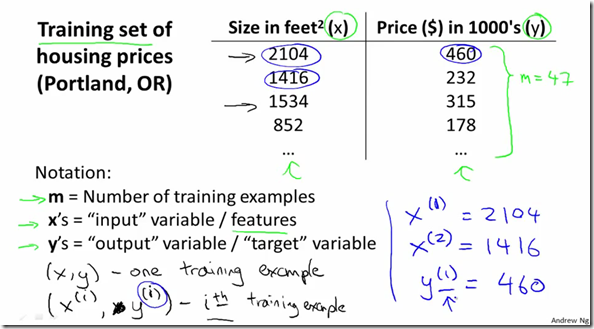
图中是某地区的面积大小与房价的关系图，输入变量X是面积，输出变量Y是房价，把已有的数据集(x,y)作为一个训练数据，拟合出线性回归模型，利用线性回归模型预测出一给定面积房子的价格。
下图1-3是典型的学习过程
图1-3 学习过程
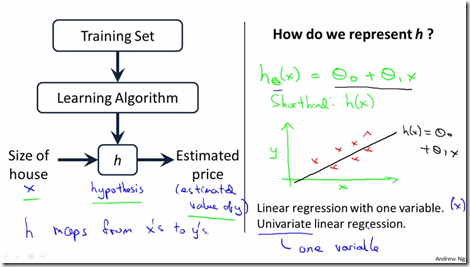
其中，h是估计函数，对应到线性回归中就是一个线性关系式
，输入变量x，经过估计函数，输出相应的估计值y。
二：代价函数
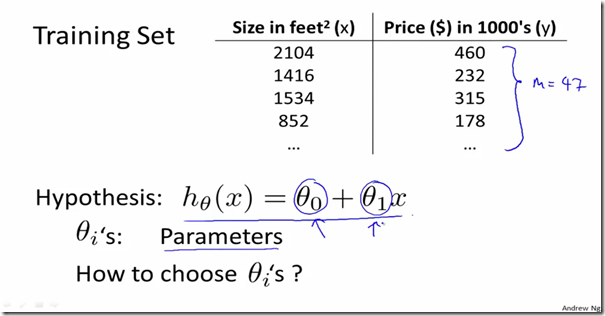
在一元线性回归中有两个参数：theta0，theta1的值是未知的，这两个参数的值决定了估计函数的好坏。估计值
与真实值y之间的差越小，说明估计函数越好，因此，选择参数theta0，theta1的标准就设为
，选择能够使得函数J（theta0,theta1）得到最小值的一对参数（theta0，theta1）作为最终的参数值。我们称函数
J（theta0,theta1）为代价函数。
下面进行举例分析，为方便理解代价函数和线性回归估计函数，先假设theta0=0，即
，给定三组训练数据（1,1）、（2,2）、（3,3），现在训练一线性回归估计函数，使得它能够最大限度的磨合训练数据，即目标是求得参数theta1的值，使得代价函数值最小，如下图所示：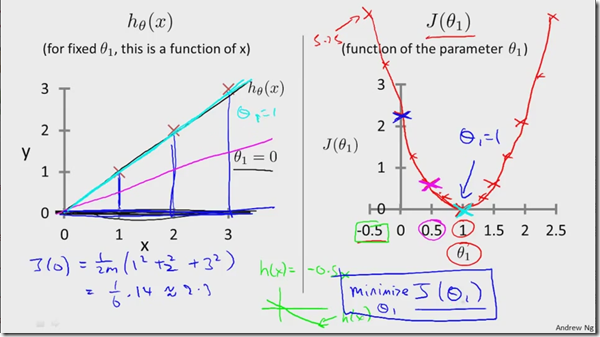 
左图是不同theta1值对应的估计函数线性图，右图是不同theta1对应的代价函数值，可以看出当theta1=1的时候，代价函数值达到了最小值0，因此最终选择theta1=1。
下面是简单的练习题：
上面设theta0=0，简单的对代价函数进行了分析，下面看下有两个参数theta0、theta1的情况：
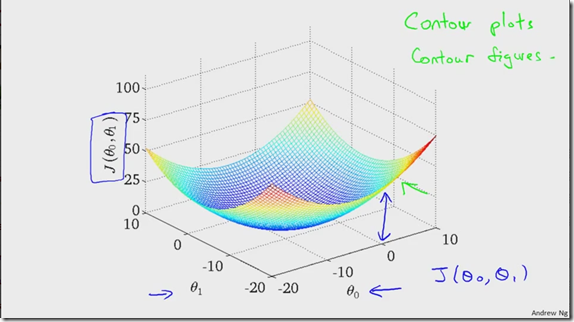
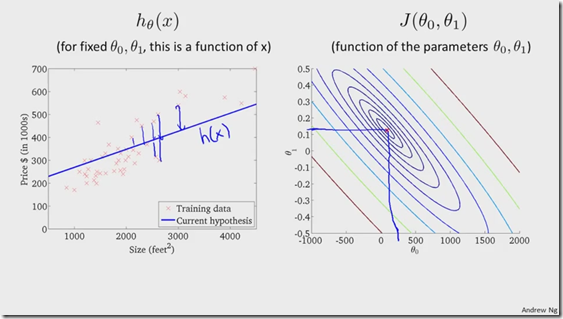
图中红色的叉叉代表训练数据，当只有参数theta1的时候，代价函数图是二维的平面图，但是当有两个参数时，代价函数就是一个三维图，如下所示：
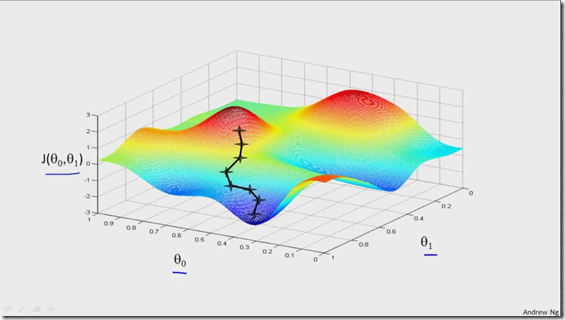
从代价函数三维图中可以看出，位于曲平面最中间的点所在的坐标（theta0，theta1）可以使得代价函数值取得最小值，为方便起见，把代价函数的三维图换成等高线图，即把曲平面映射到地面。如下所示：
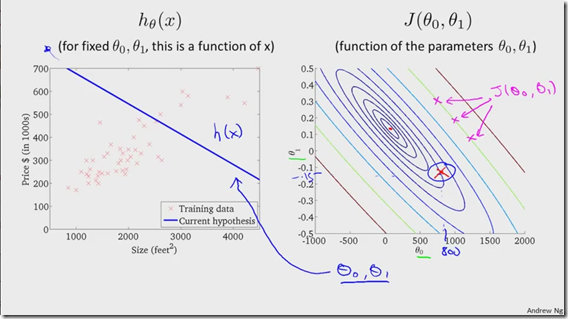
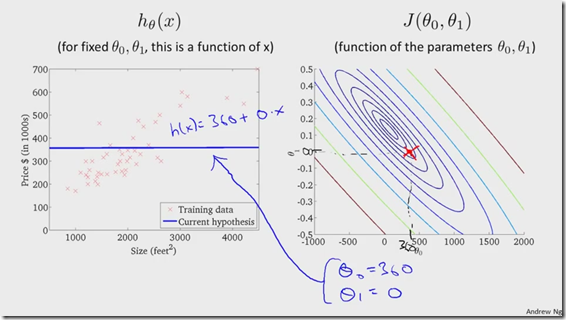
代价函数等高线图中，在相同颜色曲线上的点有相同大小的代价函数值，随着参数theta0，theta1的调整，估计函数线逐渐与训练数据重合，代价函数值逐渐变小，最终到达曲线平面的最中点。
三：梯度下降法
第二节中，我们画出代价函数关于参数theta0，theta1的图形，从图中可以大概得知取得最小代价函数值时所对应的参数值，但是当参数个数多于2个的时候，这种方法就不适用了，因此本节研究自动获取最佳参数的方法：梯度下降法。
梯度下降法是机器学习中常用的一种方法：
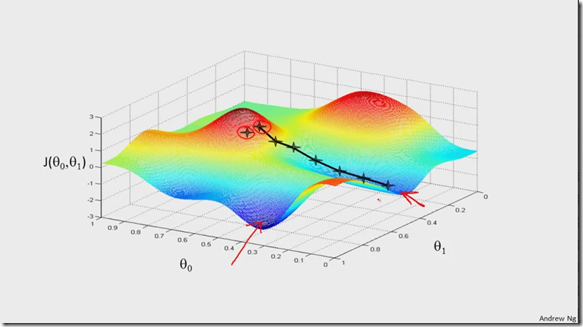
这里梯度下降法的应用可以想象成是：把代价函数图看成是一座山，从山上任意一点出发下山，在给定步伐大小情况下，需要在最快时间内走到山脚，也许不同的出发点可能到达不同的山脚，但是它们的海拔高度可能差不多。
具体的算法流程如下：
1：先给theta0，theta1设定初始值，即对应着下山的出发点。
2：设定下山步伐大小，即对应
，代表学习率。
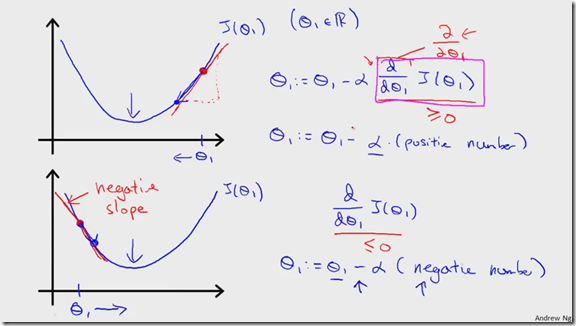
3：为了能够快速的到达山脚，在相同步伐大小情况下，往梯度最大方向走肯定最快，梯度大小也就是对应着上图中的斜率
。
4：每次都同时更新参数theta0，theta1，图中左下侧的更新公式是正确的，右下侧是错误的。
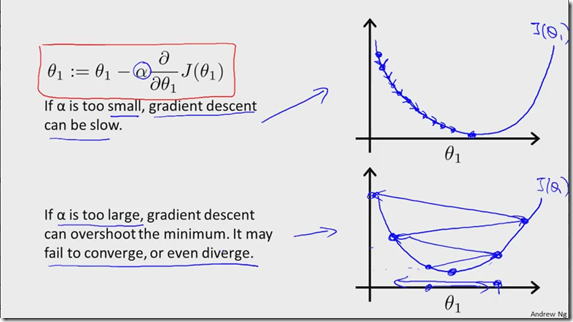
参数的大小决定了代价函数是否能够逐渐收敛到一比较小的值，下图所示：
以参数theta1的更新举例，斜率大小可能是正值也可能是负值，如果是正值则参数theta1逐渐变小，如果是负值，则参数theta1逐渐变大。
因此，如果参数太小，梯度下降的速度虽然会比较慢，但是肯定会逐渐收敛到一极小值，但是如果太大，则可能导致代价函数不能收敛到极小值，并且是两边交叉变化的，如上图所示。
四：线性回归对应的梯度下降法
下图是线性回归对应的梯度下降法，是一个不断迭代的过程。
最终的的算法流程如下：
简单测试题：
五：总结
本节主要介绍了一元线性回归、代价函数、梯度下降法，在求一元线性回归中的参数估计时，用到了梯度下降法，在下面的一章节中将进行习题练习和实验实现本节介绍的方法。
除了梯度下降法求参数估计值外，还有常用的利用最小二乘法的正规方程方法，也将在下面的章节中进行介绍和对比。