[整理]插头 dp

全名是基于连通性状态压缩的动态规划问题，从这个名字可以看出它的特征：是状压 dp（废话）、维护的是连通性。
怎么理解呢？接下来以洛谷模板题为例讲解它的维护方法。
考虑如何维护一条轮廓线，我们需要引入插头的概念：一个格子的插头是指它可以连出去的某条边（或者理解为让轮廓线插♂进来的地方）。对于这题我们应从上到下从左到右递推，就应该考虑上一行对下一行有什么影响：需要记录每一行的插头情况和连通情况（不理解没关系，下面有详细图解）。
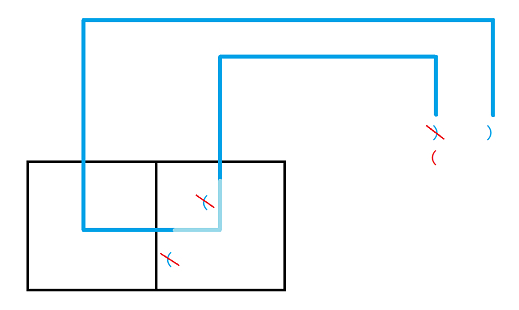
具体来说，插头情况就是每个格子有没有插头，连通情况是指每个插头对应的连通轮廓线情况。例如：下图中红线处的插头情况可以状压成 (1111)，连通情况是 ((1,2)) 连通、((3,4)) 连通。

我们很容易发现，插头之间的连通情况就像括号匹配一样不会出现交叉，由此产生了括号表示法：用左/右括号代表每个连通分量中从左边/右边插出来的插头，空代表没有插头，这样上图的连通情况又可以表示为 ( exttt{(())})，然后我们发现其实插头情况已经在连通情况中表示出来了，所以去掉这一维。
然后我们就可以大力分类讨论当前格子的左/上的插头情况了：

1. 当前格子为障碍，当且仅当都没有插头时才能转移；
2. 当前格子无障碍且都没有插头时，当前格子的右/下插头都应连接；
   
3. 有一个方向有插头时，可以选择直走或拐弯；
   
   
4. 都有插头且括号类型相同时，遍历找到对应括号转移（以都为左括号为例）；
   
5. 都有插头且左插头为右括号、上插头为左括号时，闭合插头；
   
6. 都有插头且左插头为左括号、上插头为右括号时，当且仅当转移到结尾才能闭合。
   

由于有三种标记，状压时应使用高于 (2) 的进制，为了方便位运算这里采用四进制状压。
然而我们发现这里的空间复杂度是 (mathcal O(nm4^m))，于是滚动数组。但是时空复杂度依然巨大多，我们发现有很多的状态是没用的，可以不用暴力枚举上一行转移而是用 Hash 表之类的东西存下来可行状态。
模板题核心常数巨大代码（第一次见优化比本体难写）：

const int N=100003;
int n,m,a[20][20],ex,ey,ans;
struct Edge {
  int to[2],nxt,wei[2];
}e[N];
int hd[N],cnt[2];
il void ade(int cur,int st,int val){
  int u=st%N;
  for(rg int i=hd[u];i;i=e[i].nxt){
    if(e[i].to[cur]==st)return (void)(e[i].wei[cur]+=val);
  }
  e[++cnt[cur]].to[cur]=st,e[cnt[cur]].wei[cur]=val;
  e[cnt[cur]].nxt=hd[u],hd[u]=cnt[cur];
  return;
}
#define D(st,k) (st>>(k<<1)&3)
#define G(val,k) (val<<(k<<1))
signed main(){
  Read(n),Read(m);
  for(rg int i=1;i<=n;i++){
    char ipt[20];scanf("%s",ipt+1);
    for(rg int j=1;j<=m;j++){
      if(ipt[j]=='.')a[i][j]=1,ex=i,ey=j;
    }
  }
  int cur=0,lst=1;ade(cur,0,1);
  for(rg int i=1;i<=n;i++){
    for(rg int j=1;j<=cnt[cur];j++)e[j].to[cur]<<=2;
    for(rg int j=1;j<=m;j++){
      lst=cur,cur^=1,cnt[cur]=0,memset(hd,0,sizeof(hd));
      for(rg int c=1;c<=cnt[lst];c++){
        int st=e[c].to[lst],v=e[c].wei[lst];
        int lt=D(st,j-1),up=D(st,j),now;
        if(!a[i][j]){//1
          if(!lt&&!up)ade(cur,st,v);
        }else if(!lt&&!up){//2
          now=st+G(1,j-1)+G(2,j);
          if(a[i+1][j]&&a[i][j+1])ade(cur,now,v);
        }else if(!(lt&&up)){//3
          if(lt){
            if(a[i][j+1])ade(cur,st-G(lt,j-1)+G(lt,j),v);
            if(a[i+1][j])ade(cur,st,v);
          }else {
            if(a[i+1][j])ade(cur,st+G(up,j-1)-G(up,j),v);
            if(a[i][j+1])ade(cur,st,v);
          }
        }else if(lt==up){//4
          now=st-G(lt,j-1)-G(up,j);
          if(lt==1){
            for(rg int k=j+1,tp=1;k<=m;k++){
              int u=D(st,k);
              if(u==1)tp++;
              else if(u==2)tp--;
              if(!tp){
                ade(cur,now-G(1,k),v);break;
              }
            }
          }else {
            for(rg int k=j-2,tp=1;k>0;k--){
              int u=D(st,k);
              if(u==2)tp++;
              else if(u==1)tp--;
              if(!tp){
                ade(cur,now+G(1,k),v);break;
              }
            }
          }
        }else if(lt==2&&up==1){//5
          ade(cur,st-G(lt,j-1)-G(up,j),v);
        }else if(i==ex&&j==ey)ans+=v;//6
      }
    }
  }
  cout<<ans<<endl;
  KafuuChino HotoKokoa
}