turtle库的基本使用
turtle.setup(width,height,startx,starty)
setup():设置窗体大小及位置,四个参数,后两个可选
如果没有指定后两个参数,则再屏幕中心
turtle.goto(x,y)
goto():到达某一个坐标位置

turtle.fd(d):正半轴方向运动
turtle.bk(d):负半轴方向运动
turtle.circle(r,angle):以r为半径,angle为圆心,绘制圆
turtle角度坐标系
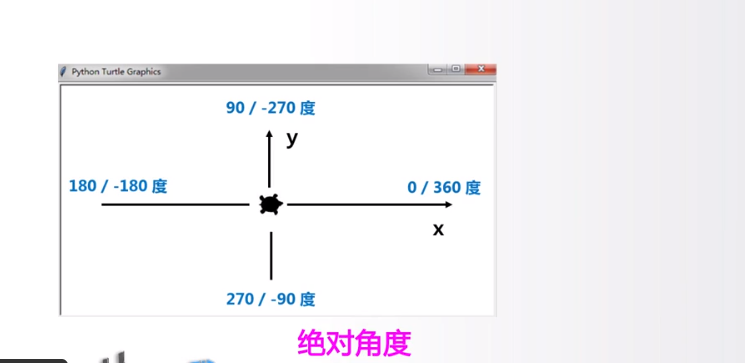
turtle.seth(angle):只改变海龟行进方向,sigle为度数
turtle.left(angle):往左偏多少度
turtle.right(angle):往右偏多少度
turtle.colormode(mode)
mode
1.0:小数模式 255:255整数模式
python中的数据类型
整数类型:
与数学中整数的概念一致,可正可负,没有取值范围限制
pow(x,y)函数:计算x的y词方,想算多少算多少
比如:pow(2,10) //1024
4种类型表示形式:
十进制: 1010,99,-217
二进制,以0B或0b开头:0B0110,-0b00100
八进制,以0O或0o开头:0O512,-0o512
十六进制,以0X或0x开头:0Xa5,-0xa5
浮点数类型:
与数学中的实数概念一致。
带有小数点及小数的数字
浮点数取值范围和小数精度都存在限制,但常规计算可忽略
取值范围数量级约-10的308次方到10的308词方,精度数量级10的-16次方
注意:浮点数间运算存在不确定位数,不是bug
例如:0.1+0.2
==》0.30000000000000004
并不是我们想要的0.3其实这是计算机的一个运算原理,很多编程语言种都有这样的问题,例如JavaScript
这时候我们想要判断0.1+0.2==0.3的时候怎么办呢?
0.1+0.2==0.3 //false
round(0.1+0.2,1)==0.3 //true
我们可以引进一个round函数,让其保留一位小数,然后再判断,结果就成为了true
round(x,d) :对x四舍五入,d是小数截取位数
浮点数也可以采用科学计数法来表示
使用字母e或E作为幂的符号,以10为技术,格式如下:
1e5:1乘以10的5次方
复数类型:
与数学中复数的概念一致,python语言中特有的数据类型
要想深度了解可百度查
操作符
加减乘除整数除 +-*/ //
+x x本身
-y y的负值
x%y 10%3结果为1
x**y 幂运算,x的y次幂
当y是小数时,开方运算10**0.5结果是根号10
与pow(x,y)效果一样
二元操作符
+= -= *= /= //= %= **=
数字运算函数
abs(x):绝对值,x的绝对值 abs(3.01) 结果为3.01
divmod(x,y):商余操作,比如divmod(10,3)结果为(3,1)
pow(x,y[,z]):幂余,(x**y)%z,[,..]表示参数z可省略。比如:pow(2,10,100)我们想要得到2的10词方的后两位数,结果为24
round(x,[,d]):默认参数d为0 ,d表示保留几位小数
max():里面参数不定,求这些数的最大值
min():里面参数不定,求这些数的最小值
int(x):将x变成整数,舍弃小数部分。int("1e2") 结果为12,必须是数字的字符串才可以,使用科学计数法也不可以。
float(x):将x变成浮点数
今天,就学习了这么多,先将笔记进行到这里,明天继续。