原本以为比较简单,但是后来发现,加能使用动态规划,算法更好。
1.题目
大家都知道斐波那契数列,现在要求输入一个整数n,请你输出斐波那契数列的第n项(从0开始,第0项为0)。n<=39。
2.分析递归方法
1 public int fib0(int n) 2 { 3 if(n<=0) 4 return 0; 5 if(n==1) 6 return 1; 7 return fib( n-1)+fib(n-2); 8 }
假设输入的是6:
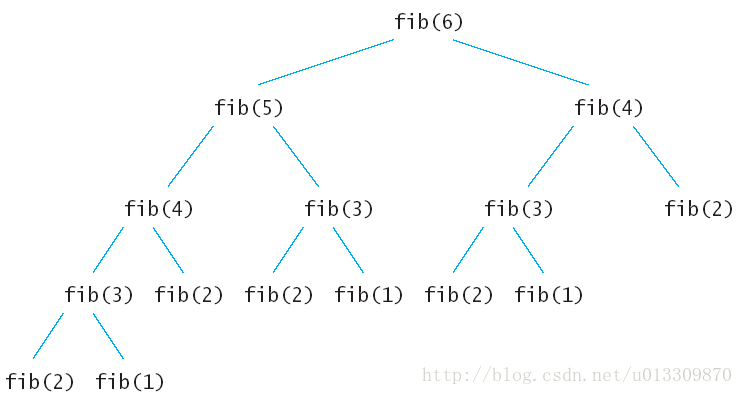
上面的递归树中的每一个子节点都会执行一次,很多重复的节点被执行,fib(2)被重复执行了5次。由于调用每一个函数的时候都要保留上下文,所以空间上开销也不小。这么多的子节点被重复执行,如果在执行的时候把执行过的子节点保存起来,后面要用到的时候直接查表调用的话可以节约大量的时间。下面就看看动态规划的两种方法怎样来解决斐波拉契数列Fibonacci 数列问题。
3.使用动态规划
①自顶向下的备忘录法
1 public static int Fibonacci(int n) 2 { 3 if(n<=0) 4 return n; 5 int [] Memo=new int[n+1]; 6 for(int i=0;i<=n;i++) 7 Memo[i]=-1; 8 return fib(n, Memo); 9 } 10 public static int fib(int n,int []Memo) 11 { 12 if(Memo[n]!=-1) 13 return Memo[n]; 14 //如果已经求出了fib(n)的值直接返回,否则将求出的值保存在Memo备忘录中。 15 if(n<=2) 16 Memo[n]=1; 17 else Memo[n]=fib( n-1,Memo)+fib(n-2,Memo); 18 return Memo[n]; 19 }
备忘录法也是比较好理解的,创建了一个n+1大小的数组来保存求出的斐波拉契数列中的每一个值,在递归的时候如果发现前面fib(n)的值计算出来了就不再计算,如果未计算出来,则计算出来后保存在Memo数组中,下次在调用fib(n)的时候就不会重新递归了。比如上面的递归树中在计算fib(6)的时候先计算fib(5),调用fib(5)算出了fib(4)后,fib(6)再调用fib(4)就不会在递归fib(4)的子树了,因为fib(4)的值已经保存在Memo[4]中。
②自底向上的动态规划
备忘录法还是利用了递归,上面算法不管怎样,计算fib(6)的时候最后还是要计算出fib(1),fib(2),fib(3)……,那么何不先计算出fib(1),fib(2),fib(3)……,呢?这也就是动态规划的核心,先计算子问题,再由子问题计算父问题。
1 public static int fib(int n) 2 { 3 if(n<=0) 4 return n; 5 int []Memo=new int[n+1]; 6 Memo[0]=0; 7 Memo[1]=1; 8 for(int i=2;i<=n;i++) 9 { 10 Memo[i]=Memo[i-1]+Memo[i-2]; 11 } 12 return Memo[n]; 13 }
③优化
自底向上方法也是利用数组保存了先计算的值,为后面的调用服务。观察参与循环的只有 i,i-1 , i-2三项,因此该方法的空间可以进一步的压缩如下。
1 public static int fib3(int n) 2 { 3 if(n<=1) 4 return n; 5 6 int Memo_i_2=0; 7 int Memo_i_1=1; 8 int Memo_i=1; 9 for(int i=2;i<=n;i++) 10 { 11 Memo_i=Memo_i_2+Memo_i_1; 12 Memo_i_2=Memo_i_1; 13 Memo_i_1=Memo_i; 14 } 15 return Memo_i; 16 }
4.完整的程序
1 package first; 2 3 public class Fibonacci { 4 public static void main(String[] args){ 5 // 6 int a=Fibonacci(3); 7 System.out.println("a="+a); 8 // 9 int b=fib(3); 10 System.out.println("b="+b); 11 } 12 13 public int fib0(int n) 14 { 15 if(n<=0) 16 return 0; 17 if(n==1) 18 return 1; 19 return fib( n-1)+fib(n-2); 20 } 21 22 23 public static int Fibonacci(int n) 24 { 25 if(n<=0) 26 return n; 27 int [] Memo=new int[n+1]; 28 for(int i=0;i<=n;i++) 29 Memo[i]=-1; 30 return fib(n, Memo); 31 } 32 public static int fib(int n,int []Memo) 33 { 34 if(Memo[n]!=-1) 35 return Memo[n]; 36 //如果已经求出了fib(n)的值直接返回,否则将求出的值保存在Memo备忘录中。 37 if(n<=2) 38 Memo[n]=1; 39 else Memo[n]=fib( n-1,Memo)+fib(n-2,Memo); 40 return Memo[n]; 41 } 42 43 public static int fib(int n) 44 { 45 if(n<=0) 46 return n; 47 int []Memo=new int[n+1]; 48 Memo[0]=0; 49 Memo[1]=1; 50 for(int i=2;i<=n;i++) 51 { 52 Memo[i]=Memo[i-1]+Memo[i-2]; 53 } 54 return Memo[n]; 55 } 56 57 public static int fib3(int n) 58 { 59 if(n<=1) 60 return n; 61 62 int Memo_i_2=0; 63 int Memo_i_1=1; 64 int Memo_i=1; 65 for(int i=2;i<=n;i++) 66 { 67 Memo_i=Memo_i_2+Memo_i_1; 68 Memo_i_2=Memo_i_1; 69 Memo_i_1=Memo_i; 70 } 71 return Memo_i; 72 } 73 74 75 76 }