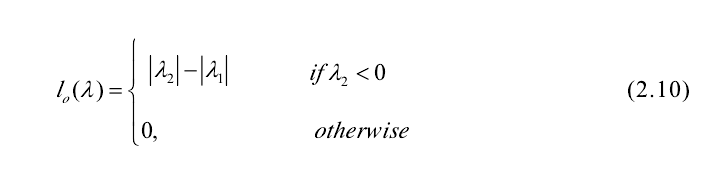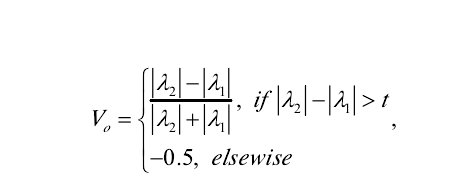Hessian矩阵以及在血管增强中的应用—OpenCV实现

有别于广为人知的Sobel、Canny等一阶算法，基于Hessian矩阵能够得到图像二阶结果，这将帮助我们深入分析图像本质。

Hessian矩阵在图像处理中有着广泛的应用：其中在图像分割领域，包括边缘检测、纹理分析等；在图像增强领域，包括边缘增强、边缘消除等。

本文从Hessian矩阵定义出发，通过清晰简洁的数学推导和讲解实现公式到C++代码的转化。

为了帮助深入理解Hessian矩阵在图像处理中的能力，我们将详细讲解和实现经典的“血管增强”算法（Frangi算法）。

 

目录：

一、Hessian矩阵等相关理论基础

1.Hessian矩阵的由来及定义

2.数字图像处理之尺度空间理论

3.基于尺度理论的Hessian简化算法

4.Hessian矩阵特征值的求解方法

5.Hessian矩阵特征值的图像性质

6.高斯方程及二阶导数

二、“血管增强”算法（Frangi算法）原理

1.认识血管及其增强

2.Frangi论文基本原理

3.Frangi论文优缺点

三、编写代码进行具体实现

1.项目结构

2.计算Hessian矩阵

3.Hessian特征值的计算

4.frangi2d主要过程

1.项目结构

2.计算Hessian矩阵

3.Hessian特征值的计算

4.frangi2d主要过程

 

需要注意的是：

1、由于本文代码基于OpenCV基础库，所以题目中添加了“OpenCV实现”字样。

2、由于图像的二维特性，所以下文中所有“Hessian矩阵”都特指“二维Hessian矩阵”。

 

一、理论基础

这里的基础理论有点多，你可以先过一遍，然后在读代码的时候再回过头来加深理解，这样效果比较好。

1. Hessian矩阵的由来及定义

由高等数学知识可知，若一元函数
在
点的某个邻域内具有任意阶导数，则

在

点处的泰勒展开式为：

，其中

，

。

二元函数

 

在

点处的泰勒展开式为：

 

其中，

。

将上述展开式写成矩阵形式，则有：

即：

其中：

 

 是 

 在  点处的Hessian矩阵。它是由函数在 点处的二阶偏导数所组成的方阵。
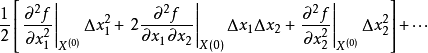
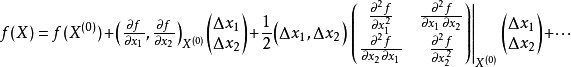
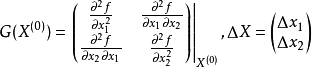
我们一般将其表示为:

 

我们也可以将其简写为：

2.数字图像处理之尺度空间理论

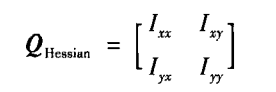
尺度空间理论的基本思想是：在图像信息处理模型中引入一个被视为尺度的参数，通过连续变化尺度参数获得多尺度下的尺度空间表示序列，对这些序列进行尺度空间主轮廓的提取，并以该主轮廓作为一种特征向量，实现边缘、角点检测和不同分辨率上的特征提取等。

尺度空间理论的特点是：将传统的单尺度图像信息处理技术纳入尺度不断变化的动态分析框架中，更容易获取图像的本质特征。尺度空间中各尺度图像的模糊程度逐渐变大，能够模拟人在距离目标由近到远时目标在视网膜上的形成过程。

尺度空间理论的一个直观理解：我们人在远近不同距离上对同一物体，都可以实现辨识。

高斯卷积核是实现尺度变换的唯一线性核（高斯函数可以称为最伟大和最重要的函数）。

一幅图像的尺度空间可以定义为：

其中符号"*"表示卷积操作。 

σ是尺度空间因子，值越小表示图像被平滑的越少，相应的尺度也就越小。大尺度对应于图像的概貌特征，小尺度对应于图像的细节特征。

 

3.基于尺度理论的Hessian简化算法

对于二维图像IHessian矩阵描述每个像素在主方向上的二维导数为：

根据尺度空间理论，二阶导数可以通过图像与高斯函数的卷积获得，例如，在点(x,y)处有

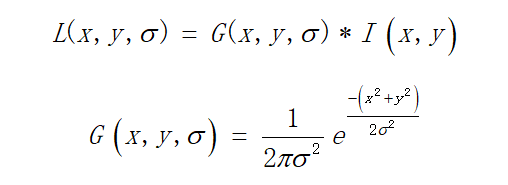
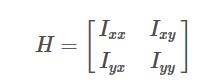
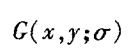其中,为尺度为的高斯函数。

如果我们接受这个理论，那么就可以得到推论：

对全图直接做偏导操作  = 对原图以特定的高斯核做卷积

基于这个推论，对于图的Hessian运算将极大地降低计算量，同时提高运算速度。

4.Hessian矩阵特征值的求解方法

首先回忆本科知识，根据定义求二阶矩阵的特征值：

根据定义，对于矩阵A，它的特征值满足

|λE-A|=0

其中

E是二阶对角阵

（1 0)

  (0 1)

我们表示A为
|a　　　b|
|c　　　d|

则λE-A|

= (λ-a)(λ-d)-bc

= λ^2-(a+d)λ+ad-bc = 0
这个是一元二次方程，可以计算得到有两个解，分别为
λ1=(a+d+√((a-d)^2+4bc))/2
λ2=(a+d-√((a-d)^2+4bc))/2 

 

由前面的资料，我们已经得到了Hessian矩阵的定义：

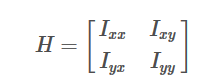
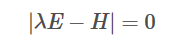
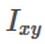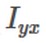
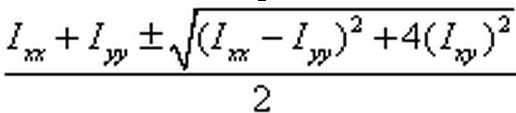
根据二维矩阵特征值的定义：“设A是n阶方阵，如果存在数m和非零n维列向量 x，使得 Ax=mx 成立，则称 m 是矩阵A的一个特征值（characteristic value)或本征值（eigenvalue)”,可以得到等式

 

并且根据图像的特性，可以得到

=

带入以上方程得到Hessian的特征值的解：

 

请记住这个结论，我们在代码部分将再一次提及。

5.Hessian矩阵特征值的图像性质

一个Hessian矩阵可以分解为两个特征值以及定义的特征向量。和

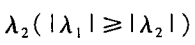
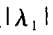其中最大的绝对特征值表示最大的局部灰度变化，其特征向量则代表它方向，可以认为是切线方向；而较小的那个代表垂直方向，也就是法线方向。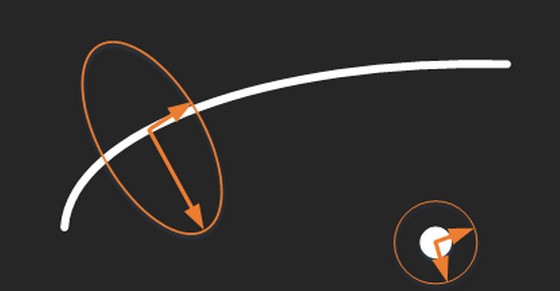

这张图可以很好地表明切线和法线的概念。

 

这些都将在下面的算法中得到利用。

 

6.高斯方程及二阶导数

前面提到了高斯函数，这里补充一些知识，下面有用。

高斯分布即正态分布，其曲线图如下：

二维高斯分布，其曲线图如下：

根据定义，我们可以求得一下内容。

二维高斯函数的一阶偏导数：

二维高斯函数的二阶偏导数

这里从原函数到二阶偏导的推断都是本科的知识，建议大家自己推一下，很简单，对于这个问题的深入认识很有帮助，后面我们在代码部分将再一次提及。

二、“血管增强”算法的原理

ujkHessian矩阵及其特征值能够很好地描述常见的几何形状的信息，我们将利用它进行血管增强；Hessian矩阵的简化算法将为我们代码化提供可能方法。我们主要基于最著名的”Frangi滤波“论文。

　　Frangi A F, Niessen W J, Vincken K L, et al. 《Multiscale vessel enhancement filtering》[C]//International Conference on Medical Image Computing and Computer-Assisted Intervention. Springer Berlin Heidelberg, 1998: 130-137. 

 

1.认识血管及其增强

在采集到的图片中，血管应该呈现“管状网络”结构，这为我们进行图像处理提供基本依据。上面提高的"Frangi"算法本身就是用来识别管线的。

2.Frangi论文基本原理

基于前面我们说明的”加速算法“，首先将血管在多尺度下进行Gaussian滤波处理，然后计算每个像素点的二阶导数构造Hessian矩阵，并且计算出两个特征值（这个地方在代码实现的时候有技巧）。

虽然我们已经得到了Hessian矩阵及其特征值，从图像上已经能够看出增强的效果，但是这还不够。接下来

将求得的特征值带入事先建立好的血管相似性函数中获取在不同尺度下的滤波响应。

 

当尺度和局部结构匹配时计算得到最大滤波响应，从而判断当前像素点是否属于血管结构。

为了尽可能地得到增强的效果，在论文中采用的是“多尺度”叠加的方法，具体来说就是采用不同的卷积核同时进行处理，得到多张处理效果，而后对结果中“着色”效果比较好的部分进行叠加。

 

3.Frangi论文优缺点

该方法得到了一种有效的血管增强方法，但是可以看到，算法中引入了较多需要认为定义的因素；同时本身较大较多的浮点运算难以在嵌入式系统上实时运行；关于”血管相似性函数“的定义缺乏理论依据，更多像是认为定义的结果，最后该算法不能够直接分割得到血管，因此该步骤往往用于血管分割的预处理阶段。

 

光看理论很难搞清楚，这里我们边讲解代码边继续理解。

 

三、编写代码，具体实现

下面开始讲解具体代码，整个可以运行的项目我会付到文章最后。在实现过程中，我们参考libfrangi https://ntnu-bioopt.github.io/software/libfrangi.html 提供的优质代码进行讲解，过程中我做了必要的精简和注释。

必须要多说一句的是，这个代码从内容到风格上，很大程度上参考了frangi的matlab版本代码https://www.mathworks.com/matlabcentral/fileexchange/24409-hessian-based-frangi-vesselness-filter，如果你也擅长matlab，建议对比学习。

1.项目结构

首先从结构开始说明，这样如果你有一定基础就可以自己先进行研究，然后对比我的讲解，对于学习有帮助。

这个项目很简单，除了main.cpp外，frangi算法封装到了frangi.h+frangi.cpp中，以函数形式直接提供。

int main(int argc, char *argv[]) {
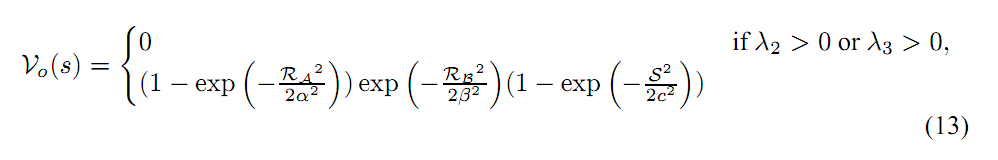
    //使用默认参数设定Frangi
    frangi2d_opts_t opts;
    frangi2d_createopts(&opts);
    //读取图片，进行处理
    Mat input_img = imread("E:/template/51.bmp", 0);
    Mat input_img_fl;
    //转换为单通道，浮点运算
    input_img.convertTo(input_img_fl, CV_32FC1);
    //进行处理
    Mat vesselness, scale, angles;
    frangi2d(input_img_fl, vesselness, scale, angles, opts);
    //显示结果
    vesselness.convertTo(vesselness, CV_8UC1, 255);
    scale.convertTo(scale, CV_8UC1, 255);
    angles.convertTo(angles, CV_8UC1, 255);
    imshow("result", vesselness);    
}

而main.cpp也尽可能简单，除了必要的图片格式转换外，主要过程封装在

 frangi2d(input_img_fl, vesselness, scale, angles, opts);

打开frangi.h，我们可以看见以下内容：

/////////////////
//Frangi filter//
/////////////////
//frangi滤波主要过程
void frangi2d(const cv::Mat &src, cv::Mat &J, cv::Mat &scale, cv::Mat &directions, frangi2d_opts_t opts);
////////////////////
//Helper functions//
////////////////////
//计算Hessian矩阵 with parameter sigma on src, save to Dxx, Dxy and Dyy. 
void frangi2d_hessian(const cv::Mat &src, cv::Mat &Dxx, cv::Mat &Dxy, cv::Mat &Dyy, float sigma);
//参数设置 (sigma_start = 3, sigma_end = 7, sigma_step = 1, BetaOne = 1.6, BetaTwo 0.08)
void frangi2d_createopts(frangi2d_opts_t *opts);
//计算特征值 from Dxx, Dxy, Dyy. Save results to lambda1, lambda2, Ix, Iy. 
void frangi2_eig2image(const cv::Mat &Dxx, const cv::Mat &Dxy, const cv::Mat &Dyy, cv::Mat &lambda1, cv::Mat &lambda2, cv::Mat &Ix, cv::Mat &Iy);

保持的是一个主要函数+三个Helper函数的过程。

2.计算Hessian矩阵

我们来看frangi2d_hessian这个函数，正如注释说明，它就是Hessian运算的具体实现：

//计算Hessian矩阵 with parameter sigma on src, save to Dxx, Dxy and Dyy.   
void frangi2d_hessian(const cv::Mat &src, cv::Mat &Dxx, cv::Mat &Dxy, cv::Mat &Dyy, float sigma);

 

其中比较难以理解的是这段，似乎做了较多的数值计算

for (int x = -round(3*sigma); x <= round(3*sigma); x++){
        j=0;
        for (int y = -round(3*sigma); y <= round(3*sigma); y++){
            kern_xx_f[i*n_kern_y + j] = 1.0f/(2.0f*M_PI*sigma*sigma*sigma*sigma) * (x*x/(sigma*sigma) - 1) * exp(-(x*x + y*y)/(2.0f*sigma*sigma));
            kern_xy_f[i*n_kern_y + j] = 1.0f/(2.0f*M_PI*sigma*sigma*sigma*sigma*sigma*sigma)*(x*y)*exp(-(x*x + y*y)/(2.0f*sigma*sigma));
            j++;
        }
        i++;
    }
    for (int j=0; j < n_kern_y; j++){
        for (int i=0; i < n_kern_x; i++){
            kern_yy_f[j*n_kern_x + i] = kern_xx_f[i*n_kern_x + j];
        }
    }

 

看上去比较奇怪。这里由于代码比较长难以理解，实际上它是在计算Dxx等的卷积核。首先我们回忆一下在理论阶段得到的一个重要结论：

 

对全图直接做偏导操作  = 对原图以特定的高斯核做卷积

这里我们就是首先把“特定的高斯核”计算出来。然后我们回忆当时介绍的二维高斯函数的二阶偏导数

 

那么它翻译成代码是什么样子的了？matlab版本

//生成卷积核
    //DGaussxx = 1/(2*pi*Sigma^4) * (X.^2/Sigma^2 - 1) .* exp(-(X.^2 + Y.^2)/(2*Sigma^2));  
    //DGaussxy = 1/(2*pi*Sigma^6) * (X .* Y)           .* exp(-(X.^2 + Y.^2)/(2*Sigma^2));
    //DGaussyy = DGaussxx';

 

c++(opencv)版本

    cv::Mat tmp1 = 1/(2*PI*Sigma*Sigma*Sigma*Sigma)*(EWM(X,X)/(Sigma*Sigma)-1);
    cv::Mat tmp2 = -1*((EWM(X,X)+EWM(Y,Y))/(2*Sigma*Sigma));
    exp(tmp2,tmp2);

 

这样你就能够理解这段代码的含义了。接下来我们就是需要用这3个特定的卷积核进行卷积

flip(Mat(n_kern_y, n_kern_x, CV_32FC1, kern_xx_f), kern_xx, -1);

 

这个地方，关于OpenCV的filter2D  函数是如何实现卷积的，和Matlab有何区别，可以参考《实际比较filter2D和imfilter之间的关系》

 

3.Hessian特征值的计算

我们回忆一下最前面得到的结论：

然后就可以理解这里的代码：

//calculate eigenvectors of J, v1 and v2
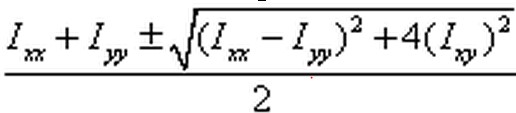
    Mat tmp, tmp2;
    tmp2 = Dxx - Dyy;
    sqrt(tmp2.mul(tmp2) + 4*Dxy.mul(Dxy), tmp);
    Mat v2x = 2*Dxy;
    Mat v2y = Dyy - Dxx + tmp;
    //normalize
    Mat mag;
    sqrt((v2x.mul(v2x) + v2y.mul(v2y)), mag);
    Mat v2xtmp = v2x.mul(1.0f/mag);
    v2xtmp.copyTo(v2x, mag != 0);
    Mat v2ytmp = v2y.mul(1.0f/mag);
    v2ytmp.copyTo(v2y, mag != 0);
    //eigenvectors are orthogonal
    Mat v1x, v1y;
    v2y.copyTo(v1x);
    v1x = -1*v1x;
    v2x.copyTo(v1y);
    //compute eigenvalues
    Mat mu1 = 0.5*(Dxx + Dyy + tmp);
    Mat mu2 = 0.5*(Dxx + Dyy - tmp);

基本上就是将数学公式翻译成为了代码，注意一下.mul是OpenCV中的“点乘”方法。

注意：

tmp2 = Dxx - Dyy; 

sqrt(tmp2.mul(tmp2) + 4*Dxy.mul(Dxy), tmp);

也就是

tmp = 

 

4.frangi2d主要过程

下面我们着重讲解

void frangi2d(const Mat &src, Mat &maxVals, Mat &whatScale, Mat &outAngles, frangi2d_opts_t opts)

函数，它是整个Frangi算法的主要过程。

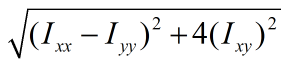
for (float sigma = opts.sigma_start; sigma <= opts.sigma_end; sigma += opts.sigma_step){……}

//多尺度叠加
    for (int i=1; i < ALLfiltered.size(); i++){
        maxVals = max(maxVals, ALLfiltered[i]);
        whatScale.setTo(sigma, ALLfiltered[i] == maxVals);
        ALLangles[i].copyTo(outAngles, ALLfiltered[i] == maxVals);
        sigma += opts.sigma_step;
    }

程序最外面的框架告诉我们，整个程序是多次运算（尺度）的叠加。

   //根据论文定义，对结果进行修正

        Dxx = Dxx*sigma*sigma;
        Dyy = Dyy*sigma*sigma;
        Dxy = Dxy*sigma*sigma;
    
        //calculate (abs sorted) eigenvalues and vectors
        Mat lambda1, lambda2, Ix, Iy;
        frangi2_eig2image(Dxx, Dxy, Dyy, lambda1, lambda2, Ix, Iy);

在每次计算中，首先计算出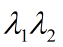的值，代码中对于的变量叫做lambda1，lambda2。

//根据定义，计算“血管增强响应函数”
        lambda2.setTo(nextafterf(0, 1), lambda2 == 0);
        Mat Rb = lambda1.mul(1.0/lambda2);
        Rb = Rb.mul(Rb);
        Mat S2 = lambda1.mul(lambda1) + lambda2.mul(lambda2);
        Mat tmp1, tmp2;
        exp(-Rb/beta, tmp1);
        exp(-S2/c, tmp2);

    //保存单尺度结果

        Mat Ifiltered = tmp1.mul(Mat::ones(src.rows, src.cols, src.type()) - tmp2);

 

这里就是Frangi算中最有价值的地方：“血管响应函数”，它的数学表示方法为：

 

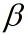其中和C都是超参数，它们在代码前面都已经根据输入参数进行了变形。

float beta = 2*opts.BetaOne*opts.BetaOne;
float c = 2*opts.BetaTwo*opts.BetaTwo;

论文中给出了参考值，代码中的变量名字都是对应的。你也可以根据修改查看。

在后来的文献中，也出现了其它“血管增强”函数，比如LiQiang

以及GVF

基于前面计算出来的特征值，这些都很容易实现。

 

四、参考文献：

1.Hessian矩阵以及在图像中的应用 https://blog.csdn.net/lwzkiller/article/details/55050275

2.血管分割技术文献综述 https://blog.csdn.net/u013102349/article/details/53819314

3.《基于Hessian矩阵和熵的CT序列图像裂缝分割方法》 王慧倩等 仪器仪表学报 2016年8月

4.百度百科 https://baike.baidu.com/item/%E9%BB%91%E5%A1%9E%E7%9F%A9%E9%98%B5/2248782?fr=aladdin

5. 数字图像处理之尺度空间理论 https://blog.csdn.net/TJC3014583925/article/details/88836485>

6. CLAHE的实现和研究 https://www.cnblogs.com/jsxyhelu/p/6435601.html

7.《实际比较filter2D和imfilter之间的关系》https://www.cnblogs.com/jsxyhelu/p/6597544.html

8.《视觉图像：高斯方程及各阶导数》https://jingyan.baidu.com/album/5bbb5a1bedf94413eba179ba.html?picindex=2

 

全部代码：

链接：https://pan.baidu.com/s/1Q0bbqkJJSHqhN7Htg3dhzQ 

提取码：gzmg

 

最后感谢大家学习至此，如果你在理解我所表述的这些内容中获得的感悟，有我写下它的时候得到的感悟的十分之一那么多，那么你一定是一名幸运的读者。