之前的Prim算法是基于顶点查找的算法,而Kruskal则是从边入手。
通俗的讲:就是希望通过 边的权值大小 来寻找最小生成树。(所有的边称为边集合,最小生成树形成的过程中的顶点集合称为W)
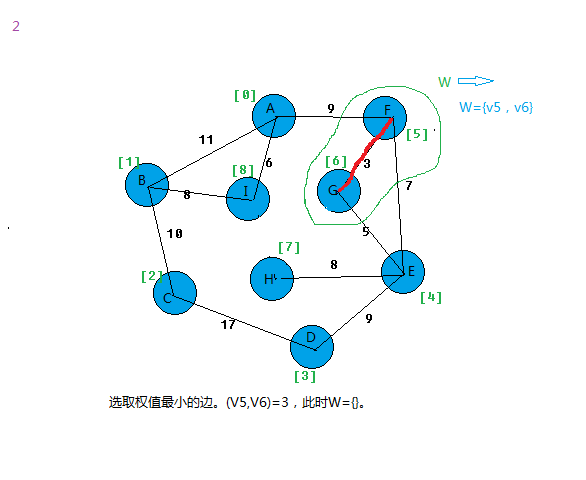
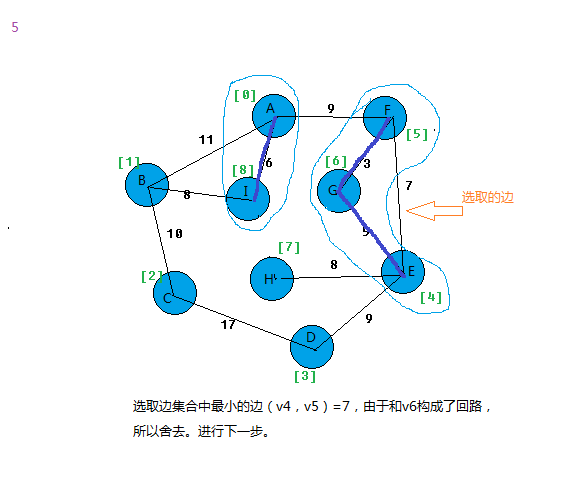
选取边集合中权值最小的边,查看边的两个顶点是否能和集合W构成环路,若能构成环路,则舍去;否则选取下一条最小权值边重复上一步。
这里需要注意一个问题,我们从最小权值的边开始寻找最小生成树,
判断当即将选入的边的两个顶点是否会和已经在集合中的顶点构成环路,这个是我们需要解决的问题。
先说下Kruskal算法的数学语言:
假设连通网N={V,{E}},则令最小生成树的初始状态只有n个顶点而无边的非连通图(T=(V,{})),图中每个顶点自成一个连通分量。
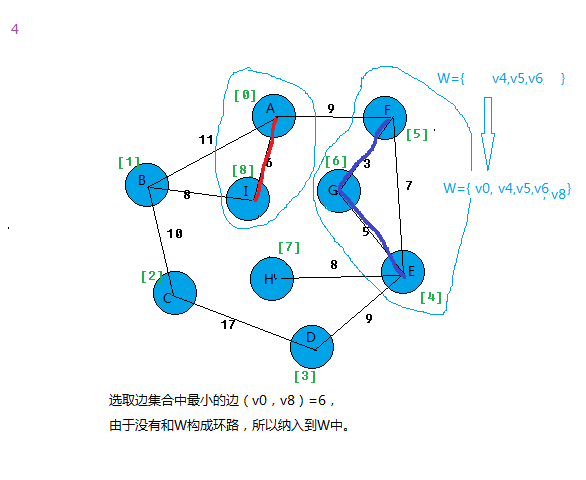
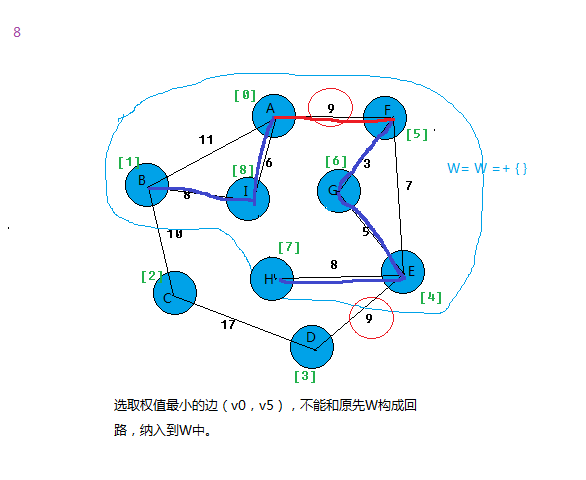
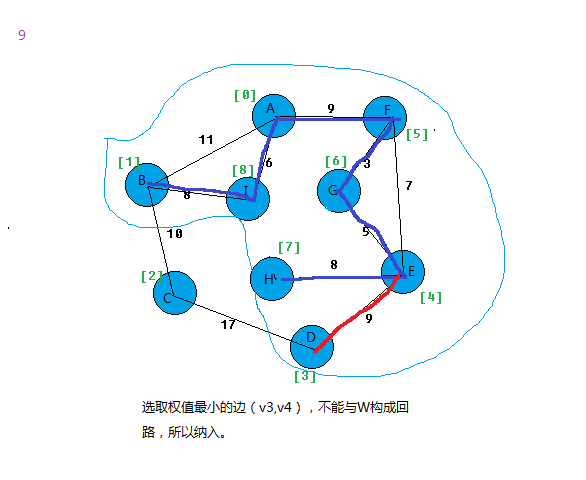
在E中选择代价最小的边,若该边依附的顶点落在T中不同的连通分量上,则将此边加入到T中,否则舍去此边而选择下一条代价最小的边。
依次类推,直到T中所有顶点都在同一连通分量上为止。
过程:
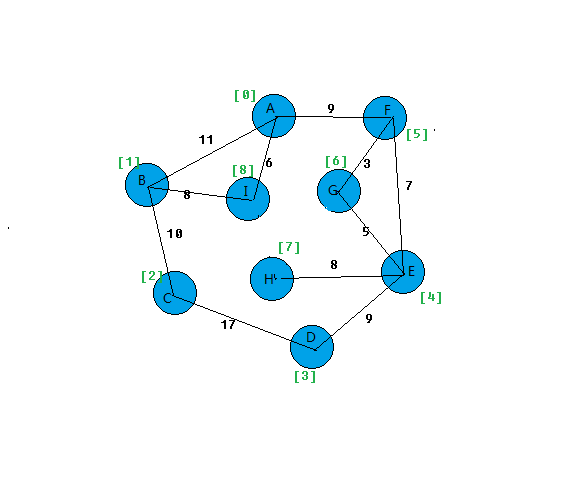

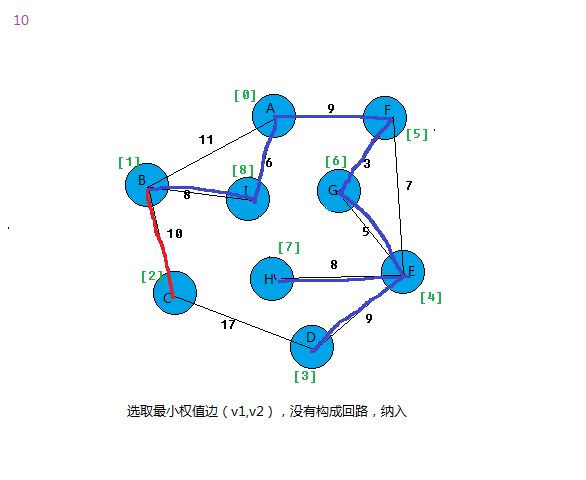

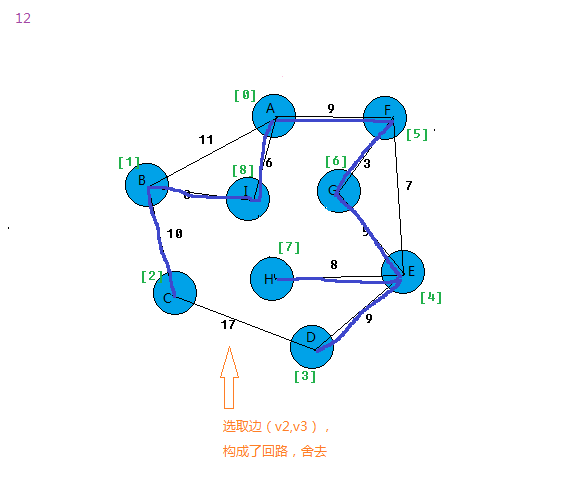
问题:
1.边的存储和排序。
2.判断新边是否会形成环路。
问题1比较好解决。可以用一个结构来存放,然后从小到大排序。
问题2比较麻烦:
怎么通过一个方法来判断新加入的边是否对已经归纳好的边形成环路。总是有牛人想出一些非常巧妙的方法,向他们致敬。
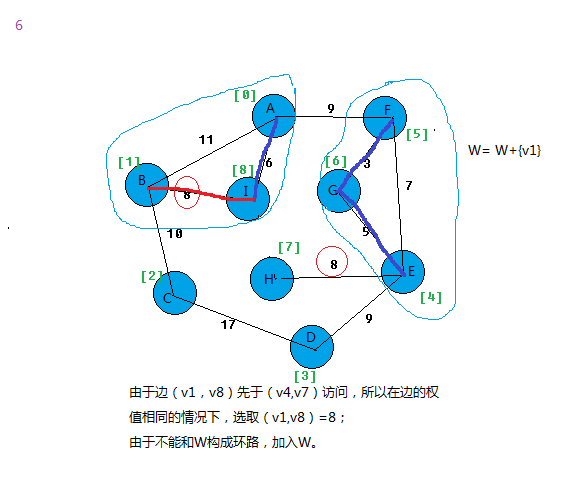
以我的图为例,我第一次出现环路的边是在第五幅图:
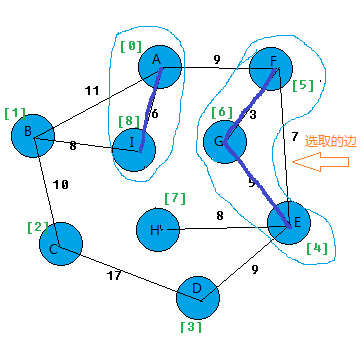
如果我们建立边的结构时候,将下标数字小的作为起点,数字大的作为终点。比如边(v5,v6)存放格式为
start:5,end:6,weight:3。
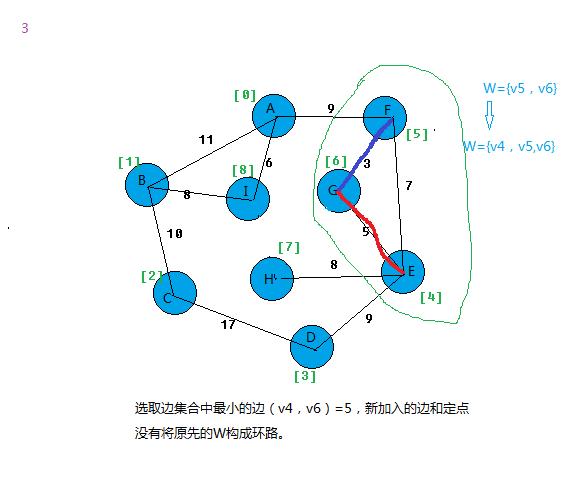
同理边(v4,v6)
start:4,end:6,weight:5。
当我们找到边(v4,v5)的时候,怎么可以让这条线被舍弃。刚才我们设置的路线上看,v4——>v6,v5——>v6是否可以通过这样的指向方式来确定两个点是否连通?
这样,如果v4和v5的边被选中,则会出现 v4,v5,v6三个点构成环路。这样我们可以用一个数组来指示Vx点所指示下一个点的下标,递归的遍历该下标,直到找到连接该点的终点。
所以,当一个边是否被选入,此时递归寻找他的两个顶点最终的指向,如果不相等则表示不会构成回路;若相等,则表示构成了回路,需要舍弃。
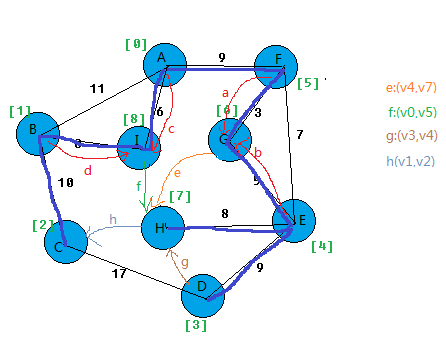
上图中的箭头线是表示该顶点记录指向的顶点。旁边说明: 比如 e在图中是由(v6,v7),而实际上是边(v4,v7)。
比如边(v2,v3),v3->v7->v2 与 v2 相等了,所以要舍弃这条边。
代码:
int findsrc(int i) { while (g_vexto[i]) { i = g_vexto[i]; } return i; } void kruskal(MGraph g,Edges *p) { int i,j; int length=0; int m,n; for (i=0;i<g.numEdges;i++) { m = p[i].start; n = p[i].end; printf("(%d,%d)",m,n); m=findsrc(m); n=findsrc(n); printf("find:(%d,%d)",m,n); if (m != n) { g_vexto[m]=n; length += p[i].weight; printf("--->(%d,%d)--->\n",p[i].start,p[i].end); } else { printf("\n"); } } printf("length:%d\n",length); }
这里调用的前提是 Edges *p 是按照权值的递增排列的。
按照之前讲解的过程,编写不难。
完整代码:
// grp-kruskal.cpp : 定义控制台应用程序的入口点。 // #include "stdafx.h" #include <stdlib.h> #define MAXVEX 100 #define IFY 65535 typedef char VertexType; typedef int EdgeType; bool g_visited[MAXVEX]; int g_vexto[MAXVEX]; VertexType g_init_vexs[MAXVEX] = {'A','B','C','D','E','F','G','H','I'}; EdgeType g_init_edges[MAXVEX][MAXVEX] = { {0,11,IFY,IFY,IFY,9,IFY,IFY,6}, //'A' {11,0,10,IFY,IFY,IFY,IFY,IFY,8}, //'B' {IFY,10,0,17,IFY,IFY,IFY,IFY,IFY},//'C' {IFY,IFY,17,0,9,IFY,IFY,IFY,IFY},//'D' {IFY,IFY,IFY,9,0,7,5,8,IFY}, //'E' {9,IFY,IFY,IFY,7,0,3,IFY,IFY}, //'F' {IFY,IFY,IFY,IFY,5,3,0,IFY,IFY}, //'G' {IFY,IFY,IFY,IFY,8,IFY,IFY,0,IFY}, //'H' {6,8,IFY,IFY,IFY,IFY,IFY,IFY,0}, //'I' }; //========================================================================== //静态图-邻接矩阵 typedef struct { VertexType vexs[MAXVEX]; EdgeType Mat[MAXVEX][MAXVEX]; int numVexs,numEdges; }MGraph; typedef struct { EdgeType weight; int start; int end; }Edges; //==================================================================== //打印矩阵 void prt_maxtix(EdgeType *p,int vexs) { int i,j; for (i=0;i<vexs;i++) { printf("\t"); for (j=0;j<vexs;j++) { if( (*(p + MAXVEX*i + j)) == IFY) { printf(" $ "); } else { printf(" %2d ", *(p + MAXVEX*i + j)); } } printf("\n"); } } //check the number of vextex int getVexNum(VertexType *vexs) { VertexType *pos = vexs; int cnt=0; while(*pos <= 'Z' && *pos >= 'A') { cnt++; pos++; } return cnt; } bool checkMat(EdgeType *p,VertexType numvex) { int i,j; for (i=0;i<numvex;i++) { for(j=i+1;j<numvex;j++) { //printf("[%d][%d] = %d\t",i,j,*(p + MAXVEX*i + j)); //printf("[%d][%d] = %d\n",j,i,*(p + MAXVEX*j + i)); if (*(p + MAXVEX*i + j) != *(p + MAXVEX*j +i) ) { printf("ERROR:Mat[%d][%d] or Mat[%d][%d] not equal!\n",i,j,j,i); return false; } } } return true; } void init_Grp(MGraph *g,VertexType *v,EdgeType *p) { int i,j; // init vex num (*g).numVexs = getVexNum(v); //init vexter for (i=0;i<(*g).numVexs;i++) { (*g).vexs[i]=*v; v++; } //init Mat for (i=0;i<(*g).numVexs;i++) { for (j=0;j<(*g).numVexs;j++) { (*g).Mat[i][j] = *(p + MAXVEX*i + j); } } if(checkMat(&((*g).Mat[0][0]),(*g).numVexs) == false) { printf("init error!\n"); exit(0); } } void CountEdge(MGraph *g) { int i,j; int cnt=0; for (i=0;i<(*g).numVexs;i++) { for (j=0;j<(*g).numVexs;j++) { if ((*g).Mat[i][j] == 0) { break; } else { if ((*g).Mat[i][j] != IFY) { //printf("[%d][%d]=%d\n",i,j,(*g).Mat[i][j]); cnt++; } } } } (*g).numEdges=cnt; printf("num edges is %d\n",cnt); } void TranMatToEdges(MGraph g,Edges **e) { int i,j; int cnt=0; *e = (Edges*)malloc(g.numEdges*sizeof(Edges)); for (i=0;i<g.numVexs;i++) { for (j=0;j<g.numVexs;j++) { if (g.Mat[i][j] == 0) { break; } else { if (g.Mat[i][j] != IFY) { (*e)[cnt].start=j; (*e)[cnt].end = i; (*e)[cnt].weight = g.Mat[i][j]; cnt++; } } } } } void sortByWeight(Edges **edge,int len) { int i,j; Edges temp; for (i=0;i<len;i++) { for (j=i+1;j<len;j++) { //printf("cmp:%d,%d\n",(*edge)[i].weight,(*edge)[j].weight); if ((*edge)[i].weight > (*edge)[j].weight) { temp = (*edge)[j]; (*edge)[j]=(*edge)[i]; (*edge)[i]=temp; } } } } int findsrc(int i) { while (g_vexto[i]) { i = g_vexto[i]; } return i; } void kruskal(MGraph g,Edges *p) { int i,j; int length=0; int m,n; for (i=0;i<g.numEdges;i++) { m = p[i].start; n = p[i].end; printf("(%d,%d)",m,n); m=findsrc(m); n=findsrc(n); printf("find:(%d,%d)",m,n); if (m != n) { g_vexto[m]=n; length += p[i].weight; printf("--->(%d,%d)--->\n",p[i].start,p[i].end); } else { printf("\n"); } } printf("length:%d\n",length); } int _tmain(int argc, _TCHAR* argv[]) { MGraph grp; //init init_Grp(&grp,g_init_vexs,&g_init_edges[0][0]); Edges *pedges=NULL; //print Matix prt_maxtix(&grp.Mat[0][0],grp.numVexs); CountEdge(&grp); TranMatToEdges(grp,&pedges); int i; sortByWeight(&pedges,grp.numEdges); for (i=0;i<grp.numEdges;i++) { printf("(%d,%d),%d\n",pedges[i].start,pedges[i].end,pedges[i].weight); } printf("kruskal\n"); kruskal(grp,pedges); getchar(); return 0; }
结果:
