递归转循环的通用方法

转载请注明出处：http://blog.csdn.net/tobewhatyouwanttobe/article/details/51180977

1.递归

定义：程序调用自身的编程技巧称为递归。

栈与递归的关系：递归是借助于系统栈来实现的。每次递归调用，系统都要为该次调用分配一系列的栈空间用于存放此次调用的相关信息：返回地址，局部变量等。当调用完成时，就从栈空间内释放这些单元，在该函数没有完成前，分配的这些单元将一直保存着不被释放。

2.递归转化为循环

记得有人说过“所有递归都能转化为循环”，某晚睡不着思考了一下这个问题，通过几天的努力，查阅了一些资料，这里结合三个例子给出解决思路，欢迎讨论。

既然系统是根据栈来实现递归的，我们也可以考虑模拟栈的行为来将递归转化为循环，

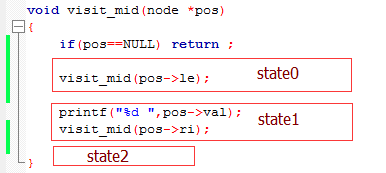
比如二叉树的中序遍历代码：

我们可以建个栈，栈保存每次递归的状态（结构体record），包括所有局部变量的值。
现在有两个问题：
1.怎样模拟递归的调用，当前进入哪个递归环境。
2.怎样保证栈中状态出入栈的顺序和递归的顺序一致。

问题1：我们用一个record cur来记录当前的递归环境，相当于每次递归的传参，发生递归调用时改变cur相应的值。
问题2：我们将这个递归函数划分为（递归调用+1）种情况，如上图划分为3种情况，state0：进入pos->le递归;state1:输出当前点，进入pos->ri递归;state2：返回。当进入一个递归体时，遇到递归dg1，处理该state应该做的事，然后构造该递归状态和state，入栈，再更新cur进入下一层。

因为cur进入下一层后的递归都要比dg1先执行（即cur进入下一层后的递归全部返回后才执行dg1），栈是先进后出，所以我们将该递归状态入栈能够保证第二点。如果一个调用结束了，就需要返回上一层，即本例的state2，作用相当于确定当前进入哪个递归环境，当前肯定是进入栈顶环境，直接将栈顶的记录弹出，来更新cur即可。说的有点多，结合完整代码看更好懂一些。

3.二叉树遍历代码：

#include <stdio.h>
#include <stdlib.h>
#include <stack>
#include <algorithm>
using namespace std;
 
struct node
{
    int val;
    node *le,*ri;
};
struct record
{
    node* a;
    int state;
    record(node* a,int state):a(a),state(state) {}
};
 
void non_recursive_inorder(node* root) //循环中序遍历
{
    stack<record> s;
    node* cur=root;   //初始化状态
    int state=0;
    while(1)
    {
        if(!cur)                 //如果遇到null结点，返回上一层 对应递归中的if(pos==NULL) return ;
        {
            if(s.empty()) break; //如果没有上一层，退出循环
            cur=s.top().a;
            state=s.top().state; //返回上层状态
            s.pop();
        }
        else if(state == 0)      //state0，执行第一个递归inorder(cur->le);
        {
            s.push(record(cur,1));//保存本层状态
            cur=cur->le;        //更新到下层状态
            state=0;
        }
        else if(state == 1)        //state1，执行print和inorder(cur->ri)
        {
            printf("%d ",cur->val);
            s.push(record(cur,2));   //保存本层状态
            cur=cur->ri;         //进入下层状态
            state=0;
        }
        else if(state == 2)        //state2，函数结束，返回上层状态
        {
            if(s.empty())break;    //初始结点的退出状态，遍历结束
            cur=s.top().a;         //返回上层状态
            state=s.top().state;
            s.pop();
        }
    }
    putchar('
');
}
 
void build(node **pos,int val)  //建二叉树
{
    if(*pos==NULL)
    {
        *pos=(node *)malloc(sizeof(node));
        (*pos)->val=val;
        (*pos)->le=(*pos)->ri=NULL;
        return ;
    }
    if(val<(*pos)->val) build(&((*pos)->le),val);
    else if(val>(*pos)->val) build(&((*pos)->ri),val);
}
void Del(node *pos)  //删除二叉树
{
    if(pos==NULL) return;
    Del(pos->le);
    Del(pos->ri);
    free(pos);
}
void visit_mid(node *pos) //递归中序遍历
{
    if(pos==NULL) return ;
    visit_mid(pos->le);
    printf("%d ",pos->val);
    visit_mid(pos->ri);
}
int main()
{
    int i,n,x;
    while(~scanf("%d",&n))
    {
        node *root=NULL;
        for(i=1; i<=n; i++)
        {
            scanf("%d",&x);
            build(&root,x);
        }
        puts("递归中序遍历:");
        visit_mid(root);
        puts("");
        puts("循环中序遍历:");
        non_recursive_inorder(root);
        Del(root);
    }
    return 0;
}
/*
9
5 2 1 4 3 8 6 7 9
*/

可以画出递归的调用和返回的图，手动模拟代码运行，看每一步cur和栈里面的状态时怎样的，能够帮助更好的理解这种思想。

若要将中序改成先序和后序，也只用改变代码中的printf的位置即可，知道每个state要做什么事情就行。

4.快速排序：

快速排序是分治、递归经典应用，一般的写法都是递归，因为其代码简单易懂，我们不妨也用上述思路来转化为循环版本，因为递归的形式和二叉树的遍历基本一致，也只需划分为3种情况即可。

代码：

#include <iostream>
#include <cstdio>
#include <cstring>
#include <stack>
#define maxn 1005
using namespace std;
 
int a[maxn];
 
struct record
{
    int le,ri,state;
    record(int le=0,int ri=0,int state=0):le(le),ri(ri),state(state){}
};
 
int Partition(int le,int ri) //划分
{
    int tmp=a[le],pos=le;
    while(le<ri)
    {
        while(le<ri&&a[ri]>=tmp) ri--;
        a[pos]=a[ri];
        pos=ri;
        while(le<ri&&a[le]<=tmp) le++;
        a[pos]=a[le];
        pos=le;
    }
    a[pos]=tmp;
    return pos;
}
void Qsort(int le,int ri) //递归版本
{
    if(le<ri)
    {
        int p=Partition(le,ri);
        Qsort(le,p-1);
        Qsort(p+1,ri);
    }
}
void QsortLoop(int n) //循环版本
{
    int i;
    record cur(1,n,0),now;
    stack<record>s;
    while(1)
    {
        //getchar();
        //printf("%d %d %d
",cur.le,cur.ri,cur.state);
        if(cur.le<cur.ri)
        {
            if(cur.state==0) //划分 向下递归 保存本层下次递归状态
            {
                int p=Partition(cur.le,cur.ri);
                now.le=p+1; now.ri=cur.ri; now.state=1;
                s.push(now);
                cur.ri=p-1;
            }
            else if(cur.state==1) //向下递归 保存本层下次递归状态
            {
                now=cur; now.state=2;
                s.push(now);
                cur.state=0;
            }
            else
            {
                if(s.empty()) break ; //栈内没有节点退出
                cur=s.top();
                s.pop();
            }
        }
        else //递归返回
        {
            if(s.empty()) break ; //栈内没有节点退出  不加这句可以试一试2 1 2
            cur=s.top();
            s.pop();
        }
    }
}
int main()
{
    int i,n;
    while(~scanf("%d",&n))
    {
        for(i=1;i<=n;i++) scanf("%d",&a[i]);
        //Qsort(1,n);
        QsortLoop(n);
        for(i=1;i<=n;i++)
        {
            printf("%d ",a[i]);
        }
        puts("");
    }
    return 0;
}
/*
5
1 2 3 4 5
7
5 10 8 6 3 20 2
6
64 5 3 45 6 78
*/

5.输出1~n的全排列。

首先来看一下循环的版本，初始化vis为0，调用dfs(n)即可得到结果：

int res[maxn];    //答案数组
bool vis[maxn];   //标记数组
void dfs(int pos) //当前进行到pos位置
{
    if(pos==n+1)  //为n+1则得到了一组答案 输出
    {
        for(int i=1; i<=n; i++)
        {
            printf("%d ",res[i]);
        }
        puts("");
    }
    for(int i=1; i<=n; i++) //枚举当前位置可以为几
    {
        if(!vis[i]) //没有使用过 当前位置可以为i
        {
            vis[i]=1;  //标记并设置当前位置
            res[pos]=i;
            printf("vis[%d]=1 pos:%d=%d
",i,pos,i);
            dfs(pos+1);
            printf("vis[%d]=0
",i);
            vis[i]=0;  //回溯
        }
    }
}

这个递归就稍稍复杂一点了，因为一个递归体会产生几次调用时不知道的，为了让递归调用和返回清晰可见，我在递归调用前和递归调用返回后都加了一些输出，也给循环版本增加了一点难度。

产生了两个新问题：

（1）调用次数位置，不好划分状态。

解决：可以根据当前循环变量i的值设置状态state，因为根据i可以知道要进入的是哪个dfs，其实向下递归的状态可以看做一个状态的，可以统一化处理。

（2）状态返回之后的事情怎么处理？

状态的返回该方法的处理是取栈顶状态，这样就失去了返回的那个过程，返回之后的事情就不好处理了。我采用的方法是将返回之后的事情当做本层下一次递归调用之前的事情，每个状态需要增加一个变量pre记录本层上一次是调用的state是多少。

代码：

#include <iostream>
#include <cstdio>
#include <cstring>
#include <stack>
#define maxn 15
typedef long long ll;
using namespace std;
#define FLAG 1
//如果不想看见递归时的输出 将1改为0
 
int n;
int res[maxn];    //答案数组
bool vis[maxn];   //标记数组
 
struct record
{
    int pos,state,pre;
    record(int pos=0,int state=0,int pre=0):pos(pos),state(state),pre(pre){}
    void show()
    {
        printf("pos:%d state:%d pre:%d ",pos,state,pre);
    }
};
void show(stack<record> my)
{
    while(!my.empty())
    {
        my.top().show();
        my.pop();
    }
    puts("");
}
void debug(record cur,stack<record> s) //调试函数
{
    int i;
    getchar();
    printf("cur:  ");
    cur.show(); puts("");
    show(s);
    for(i=1;i<=n;i++)
    {
        printf("i:%d vis:%d  ",i,vis[i]);
    }
    puts("");
    for(i=1;i<=n;i++)
    {
        printf("i:%d res:%d  ",i,res[i]);
    }
    puts("");
}
void solve()  //循环版本
{
    int i;
    memset(vis,0,sizeof(vis));
    stack<record> s;
    record cur(1,1,0),now;
    while(1)
    {
        //debug(cur,s);
        if(cur.pos>n) // 当前位置大于n找到一组答案 输出并返回上一层
        {
            for(i=1;i<=n;i++)
            {
                printf("%d ",res[i]);
            }
            puts("");
            if(s.empty()) break; // 栈内没有节点退出
            cur=s.top();
            s.pop();
        }
        else
        {
            if(cur.state<=n) //state1~n的情况
            {
                for(i=cur.state+1;i<=n;i++)  // 找这一层下次进哪个dfs
                {
                    if(!vis[i]) break;
                }
                if(i<=n) // 本层还要递归 向下递归 保存本层下一次递归
                {
                    now=cur;  now.state=i;  now.pre=cur.state;
                    vis[cur.pre]=0;  // 将本层的上次递归的vis清0
                    #if FLAG
                        if(cur.pre) printf("vis[%d]=0
",cur.pre);
                        printf("vis[%d]=1 pos:%d=%d
",cur.state,cur.pos,cur.state);
                    #endif
                    vis[cur.state]=1;  // 标记并记录答案
                    res[cur.pos]=cur.state;
                    s.push(now);  // 本层下一次递归入栈
                    cur.pos++;    // cur更新为下一层状态
                    cur.pre=0;
                    for(i=1;i<=n;i++) // 找下一层从哪个dfs开始
                    {
                        if(!vis[i]) break;
                    }
                    cur.state=i;
                }
                else  // 该递归是本层最后一次递归 向下递归完后本层结束 返回上层
                {
                    now=cur;  now.state=n+1;  now.pre=cur.state;
                    vis[cur.pre]=0;  // 将本层的上次递归的vis清0
                    #if FLAG
                    if(cur.pre) printf("vis[%d]=0
",cur.pre);
                    printf("vis[%d]=1 pos:%d=%d
",cur.state,cur.pos,cur.state);
                    #endif // FLAG
                    vis[cur.state]=1;
                    res[cur.pos]=cur.state;
                    s.push(now);
                    cur.pos++;
                    cur.pre=0;
                    for(i=1;i<=n;i++) // 找下一层从哪个dfs开始
                    {
                        if(!vis[i]) break;
                    }
                    cur.state=i;
                }
            }
            else
            {
                #if FLAG
                    printf("vis[%d]=0
",cur.pre);
                #endif // FLAG
                if(s.empty()) break; // 栈内没有节点退出
                vis[cur.pre]=0;
                cur=s.top();
                s.pop();
            }
        }
    }
}
int main()
{
    while(~scanf("%d",&n))
    {
        solve(); //循环版本
    }
    return 0;
}
/*
3
*/

ps:代码增加了对应递归版本的中间输出，如果不希望看到，这可以把FLAG置为0.

输入3，运行可以得到如下结果，和递归版本的结果一模一样，递归的调用和返回时做的事情也清晰可见。

vis[1]=1 pos:1=1
vis[2]=1 pos:2=2
vis[3]=1 pos:3=3
1 2 3
vis[3]=0
vis[2]=0
vis[3]=1 pos:2=3
vis[2]=1 pos:3=2
1 3 2
vis[2]=0
vis[3]=0
vis[1]=0
vis[2]=1 pos:1=2
vis[1]=1 pos:2=1
vis[3]=1 pos:3=3
2 1 3
vis[3]=0
vis[1]=0
vis[3]=1 pos:2=3
vis[1]=1 pos:3=1
2 3 1
vis[1]=0
vis[3]=0
vis[2]=0
vis[3]=1 pos:1=3
vis[1]=1 pos:2=1
vis[2]=1 pos:3=2
3 1 2
vis[2]=0
vis[1]=0
vis[2]=1 pos:2=2
vis[1]=1 pos:3=1
3 2 1
vis[1]=0
vis[2]=0
vis[3]=0

思路来源于：http://blog.csdn.net/biran007/article/details/4156351