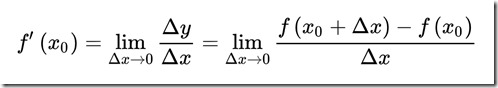在高等数学学习中,经历了初步的极限和无穷学习后,第一个重要的概念就是导数。以下是导数的定义和几何意义:
一、定义
为了能够从不同角度理解,特意摘抄不同教材和出处对于导数的定义,实质上来讲,都是描述同一个东西。
1. 网络上的描述:
设函数y=f(x)在点x0的某个邻域内有定义,当自变量x在x0处有增量Δx,(x0+Δx)也在该邻域内时,相应地函数取得增量Δy=f(x0+Δx)-f(x0);如果Δy与Δx之比当Δx→0时极限存在,则称函数y=f(x)在点x0处可导,并称这个极限为函数y=f(x)在点x0处的导数,记作① 


*来自百度百科
2. 大学教材的描述:
*来自同济版高等数学上,75页
3. 英文的描述如下 (Wiki和两本书):
In mathematics, the derivative of a function of a real variable measures the sensitivity to change of the function value (output value) with respect to a change in its argument (input value). Derivatives are a fundamental tool of calculus. For example, the derivative of the position of a moving object with respect to time is the object's velocity: this measures how quickly the position of the object changes when time advances.
* quote from Wikipedia
* quote from Calculus Early Transcendentals 10e
* quote from Calculus Schaum's Outline
二、几何意义
根据以上定义,结合函数本身的性质,我们可以得到导数的相关几何意义:函数y=f(x)在x0点的导数f'(x0)的几何意义:表示函数曲线在点P0(x0,f(x0))处的切线的斜率(导数的几何意义是该函数曲线在这一点上的切线斜率)。
数学是一个精妙的学科,她的相关概念和逻辑,只要不与自身的定义所矛盾,可以适用于所有的情况。