如果数据量过大,超过最大的内存容量,那么一次性将所有数据读入内存进行排序是不可行的。
例如,一个文件每一行存了一个整数,该文件大小为10GB,而内存大小只有512M,如何对这10GB的数据进行排序呢?
外部排序就是为了解决这种问题的。
思路:
外部排序的思路是,将超大文件分成若干部分,每一部分是可以读入内存的,例如,将10GB的文件分为40份,则每一份就只有256M。将每一份读入内存,用已知的方法进行排序(快拍,堆排等方式),再写到一个文件中。这样,我们得到了40个已序的小文件。
再采用归并(Merge)的方式,将40个文件合并为一个大文件,则这个大文件就是我们要的结果。
难点:
归并的方式是一个难点。最直观地思路是两路归并。
将40个文件编号1-40,1和2归并,3和4归并...39和40归并,生成了20个文件,再将这20个文件继续两路归并。
从40个文件变成20个文件,相当于把所有10G的数据从磁盘读出,再写到磁盘上,从20个文件到10个文件,也相当于把10G的数据从磁盘读出,再写到磁盘上。这种磁盘IO操作一共要执行6次。(2^6=64>40)
再来考虑K路归并。所谓K路归并,就是一次比较K路数据,选出最小的。例如当K=10,则是将40个文件分成1-10,11-20,21-30,31-40。对1-10,由于已序,故只要比较出这10个文件的第一个数,看哪个最小,哪个就写到新文件,再进行下一轮的比较。这样,只要2次磁盘IO就可以了。
假设我们将文件分为m份,使用K路归并,则磁盘IO的次数就是log K底m。我们当然是希望这个值越小越好。但是是不是K越大就越好呢?我们来看看算法的时间复杂度。
对于总共s个数据的K路归并,每次需比较K-1次,才能得出结果中的一个数据,s个数据就需要比较(s-1)(K-1)次
对于总共n个数据,分为m份,使用K路归并,总共需要比较 (log K底m) * (n-1)(K-1)= (logm/logK)*(n-1)(K-1) = logm*(n-1)*(K-1)/logK,当K增大时,(K-1)/logK是增大的,也即时间复杂度是上升的。因此要么K不能太大,要么找出一个新的方法,使得每次不用比较K-1次才得出结果中的一个数据。我们选择后者,这种方法就是失败树。
失败树:
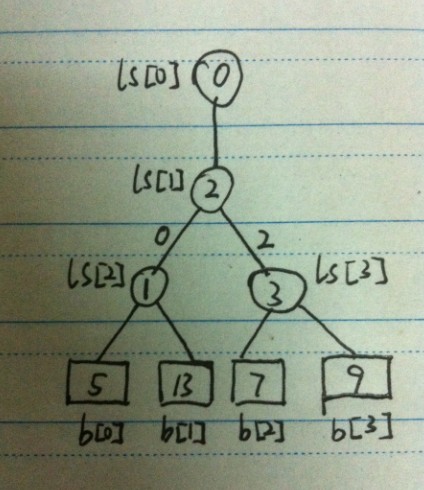
圆形的是失败树的节点,方形的是K路数据中每路数据的最小值,图上K=4。
失败树用数组ls[]存储,K路数据中没路数据的最小值用b[]存储。
失败树的性质:
失败树里的每个节点中所存的值是失败者的下标,即b[]中的一个下标。例如,b[0]和b[1]比较的失败者(我们要求出最小值,因此大的数是失败者)是b[1],ls[2]中存的就是1。
值得注意的是,我们并不是使用失败者去进行下一轮比较,而是用成功者进行下一轮比较。例如,ls[2]中虽然存的是1,但是参与下一轮比较的是b[0],同理,ls[3]中存的是下标3,但是参加下一轮比较的是b[2]。ls[1]中存放的是b[0]和b[2]比较所产生的失败者下标。获胜者的下标则存在ls[0]中,因此,b[ls[0]]是所有比较的获胜者,即这四个数中最小的。
因此,我们将b[ls[0]]写入新的文件,然后b[ls[0]]读入本路的下一个数据。
读入下一个数据之后,失败树的性质可能发生变化,我们要对数进行维护。
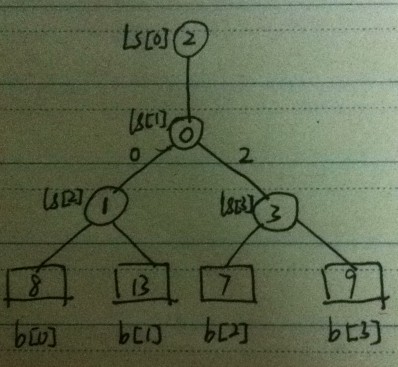
维护的过程
将新的b[ls[0]] 与失败树中的父节点进行比较。一直比到b[ls[1]],然后产生新的ls[0]
具体到本处,就是b[0]与b[ls[2]]比较,失败者为b[ls[2]],因此ls[2]不变,再将b[0]与b[ls[1]]比较,失败者为b[0],因此ls[1]更新为0,ls[0]更新为之前的ls[1]。现在新的最小值就是b[ls[0]]=b[2]=7
#include <iostream> using namespace std; #define K 4 //表示4路归并 #define MIN INT_MIN; int b[K+1] = {5,13,7,9}; int ls[K] = {0};//记录败者的下标 void Adjust(int s) { int t = (s+K)/2;//t=(s+k),得到与之相连ls数组的索引 while(t>0) { if(b[s] > b[ls[t]])//父亲节点 { int temp = s; //s保存获胜者的下标 s = ls[t]; ls[t]=temp; } t=t/2; //父节点 } ls[0] = s;//将最小节点的索引存储在ls[0] } void CreateLoser() { b[K] = MIN; int i; for(i=0;i<K;i++)ls[i]=K; for(i=K-1;i>=0;i--)Adjust(i); //加入一个基点,要进行调整 } int main() { CreateLoser(); system("pause"); return 0; }
建立失败树的过程用到了一个小技巧。首先假设各路的最小值都是MIN,MIN小于各路的最小值,失败数节点里的值可以为任意值,这里统一为K。然后从i=K-1 to o,一个一个读入b[i],并对失败树进行维护,当所有的b[i]都读入后,失败树也就建立好了。
用失败树找最小值,时间复杂度为logK,不再是K-1,因此对于总共n个数据,分为m份,使用K路归并,时间复杂度为logm * (n-1)