John 打算驾驶一辆汽车周游一个环形公路。
公路上总共有 n 个车站,每站都有若干升汽油(有的站可能油量为零),每升油可以让汽车行驶一千米。
John 必须从某个车站出发,一直按顺时针(或逆时针)方向走遍所有的车站,并回到起点。
在一开始的时候,汽车内油量为零,John 每到一个车站就把该站所有的油都带上(起点站亦是如此),行驶过程中不能出现没有油的情况。
任务:判断以每个车站为起点能否按条件成功周游一周。
输入格式
第一行是一个整数 n,表示环形公路上的车站数;
接下来 n 行,每行两个整数 pi,di,分别表示表示第 i 号车站的存油量和第 i 号车站到 顺时针方向 下一站的距离。
输出格式
输出共 n 行,如果从第 i 号车站出发,一直按顺时针(或逆时针)方向行驶,能够成功周游一圈,则在第 i 行输出 TAK,否则输出 NIE。
数据范围
$3≤n≤10^6,
\(0≤pi≤2×10^9,\)
\(0<di≤2×10^9\)
输入样例:
5
3 1
1 2
5 2
0 1
5 4
输出样例:
TAK
NIE
TAK
NIE
TAK
思路
先只考虑顺时针的情况:
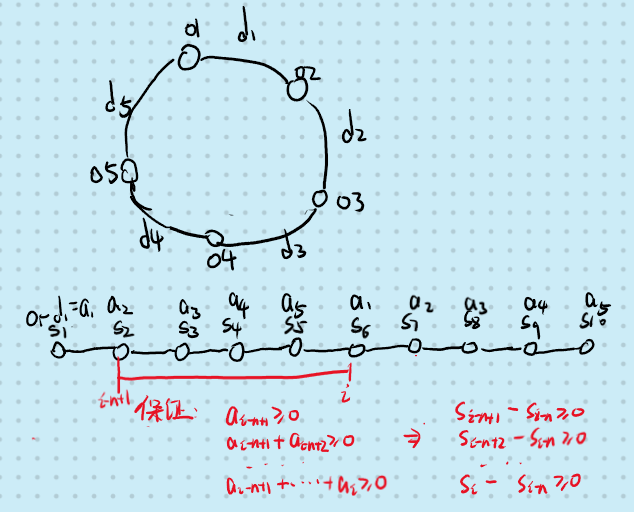
滑动窗口维护i-n+1到i的a的前缀和s的最小值和,如果最小值s[k]小于s[i-n],那么说明从k到下一点时油不够无法到达,否则从i-n+1出发符合题意。
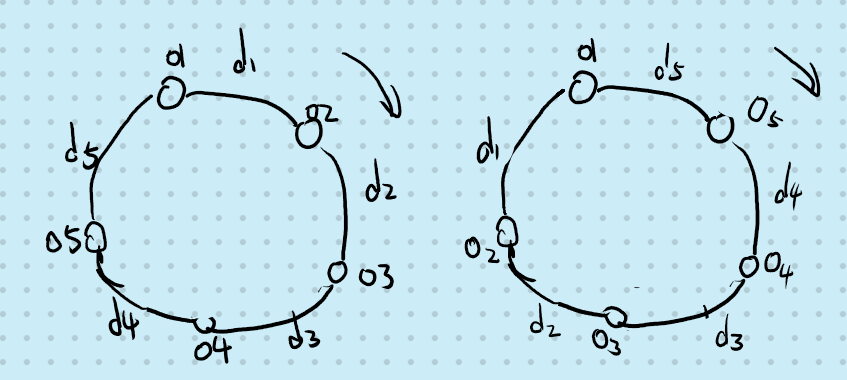
逆时针时我们可以构造一个以1点为对称轴的对称图形,然后再做一次顺时针:
代码
#pragma comment(linker, "/STACK:1024000000,1024000000")
#include <cstdio>
#include <iostream>
#include <cstring>
using namespace std;
typedef long long LL;
const int N=100010;
LL o[N*2],d[N*2],s[N*2],q[N*2];
bool st[N];
int main(int argc, char * argv[])
{
// freopen("data.in","r",stdin);
// freopen("data.out","w",stdout);
int n;
scanf("%d",&n);
for(int i=1;i<=n;++i) scanf("%lld%lld",&o[i],&d[i]);
for(int i=1;i<=n;++i) s[i]=s[i+n]=o[i]-d[i];
for(int i=1;i<=n*2;++i) s[i]+=s[i-1];
int hh=0,tt=0;
for(int i=1;i<=n*2;++i){
if(hh!=tt&&i-q[hh]>=n) ++hh;
while(hh!=tt&&s[q[tt-1]]>=s[i]) tt--;
q[tt++]=i;
if(i>=n){
if(s[q[hh]]-s[i-n]>=0){
st[i-n+1]=1;
}
}
}
for(int i=2;i<=n/2+1;++i) {
swap(o[n-i+2],o[i]);
}
for(int i=1;i<=n/2;++i){
swap(d[n-i+1],d[i]);
}
for(int i=1;i<=n;++i) s[i]=s[i+n]=o[i]-d[i];
for(int i=1;i<=n*2;++i) s[i]+=s[i-1];
hh=0,tt=0;
for(int i=1;i<=n*2;++i){
if(hh!=tt&&i-q[hh]>=n) ++hh;
while(hh!=tt&&s[q[tt-1]]>=s[i]) tt--;
q[tt++]=i;
if(i>=n){
if(s[q[hh]]-s[i-n]>=0){
st[n-(i-n+1)+2]=1;
}
}
}
for(int i=1;i<=n;++i){
if(st[i]) cout<<"TAK\n";
else cout<<"NIE\n";
}
return 0;
}