271. 杨老师的照相排列
题意:
有n个学生根据身高排队合影,一种站成k行,每行左对齐,要求左边高于右边,前面高于后面
思路:
假设我们将每个学生的身高从高到底排序,对于每个排列状态(a,b,c,d,e),都可以由最后一个加入的同学转移过来。
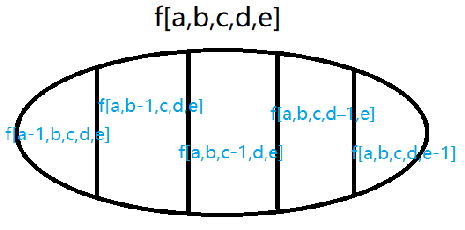
代码:
#include<iostream>
#include<string.h>
using namespace std;
typedef long long LL;
LL a[6];
LL f[31][31][31][31][31];
int main(){
int n;
while(cin>>n){
if(!n) break;
memset(a,0,sizeof a);
memset(f,0,sizeof f);
for(int i=1;i<=n;++i) cin>>a[i];
f[0][0][0][0][0]=1;
for(int a1=0;a1<=a[1];++a1){ //最后一行
for(int a2=0;a2<=min(1ll*a1,a[2]);++a2){
for(int a3=0;a3<=min(1ll*a2,a[3]);++a3){
for(int a4=0;a4<=min(1ll*a3,a[4]);++a4){
for(int a5=0;a5<=min(1ll*a4,a[5]);++a5){
LL v=f[a1][a2][a3][a4][a5];
if(a1<a[1]){
f[a1+1][a2][a3][a4][a5]+=v;
}
if(a2<a[2]&&a2+1<=a1){
f[a1][a2+1][a3][a4][a5]+=v;
}
if(a3<a[3]&&a3+1<=a2){
f[a1][a2][a3+1][a4][a5]+=v;
}
if(a4<a[4]&&a4+1<=a3){
f[a1][a2][a3][a4+1][a5]+=v;
}
if(a5<a[5]&&a5+1<=a4){
f[a1][a2][a3][a4][a5+1]+=v;
}
}
}
}
}
}
cout<<f[a[1]][a[2]][a[3]][a[4]][a[5]]<<endl;
}
return 0;
}
273. 分级
题意:
给定长度为N的序列A,构造一个长度为N的序列B,满足:
1、B非严格单调,即(B_1≤B_2≤…≤B_N)或(B_1≥B_2≥…≥B_N)。
2、最小化 (S=|A_i−B_i|)。
只需要求出这个最小值S。
思路:
一定存在一种最优解,B序列中出现的数字都是来自于A序列的。f[i,j]表示构造长度为i的B序列,第i个数字是降序排序后的(a_j),那么(f[i,j]=min(f[i-1][1)$j])+abs(a[i]-b[j])$,复杂度O(n^3)。可以开一个临时数组距离f[i-1][1j]的最小值,val变量随着第i维一起遍历。
代码:
#include<bits/stdc++.h>
using namespace std;
const int N=2010;
int f[N][N],tmp[N],a[N],b[N];
int main(){
int n;
cin>>n;
for(int i=1;i<=n;++i) cin>>a[i],b[i]=a[i];
sort(b+1,b+1+n);
memset(f,0x3f,sizeof f);
for(int i=1;i<=n;++i){
int val=tmp[1];
for(int j=1;j<=n;++j){
val=min(tmp[j],val);
f[i][j]=min(f[i][j],val+abs(a[i]-b[j]));
}
memcpy(tmp,f[i],sizeof tmp);
}
int res=0x3f3f3f3f;
for(int j=1;j<=n;++j) res=min(res,f[n][j]);
cout<<res<<endl;
return 0;
}
277. 饼干
题意:
有m块饼干分给n个小朋友,每个小朋友至少分到一块。有个小朋友都有一个贪婪度值(a_i),当一个小朋友比k个小朋友得到的饼干少,他就会产生(a_i*k)的怒气值。
求使得所有小朋友产生的最少怒气值和以及输出该分配方案。
思路:
这道题没有告诉分配顺序,但是DP问题首先要确定遍历顺序,用贪心的微调法可以得到一个结论,当(a_i>a_j),那么第i个小朋友就一定大于等于第j个小朋友分到的饼干。问题就转化成了将整数m分成n个正整数之和,这里利用900. 整数划分的分析方法,通过枚举当前状态里有至少有几个1转移。f[i][j]表示前i个小朋友分j块饼干的最小怒气值.
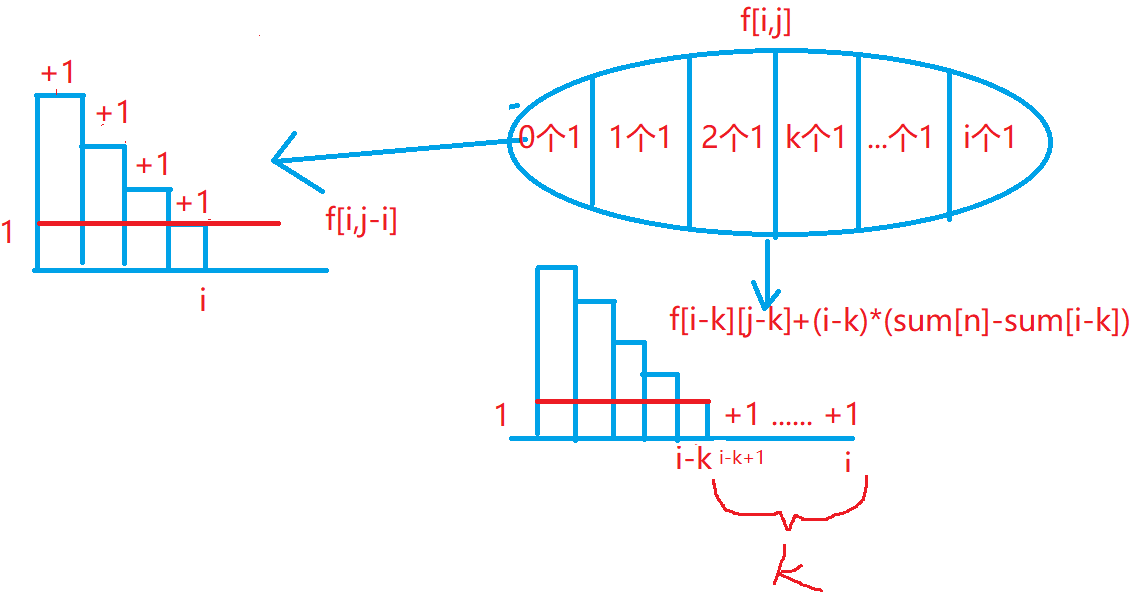
方案我们可以通过倒推得到。
代码:
#include<bits/stdc++.h>
#define x first
#define y second
using namespace std;
typedef pair<int,int> PII;
PII a[40];
int f[40][5010],sum[40],ans[40];
int main(){
int n,m;
cin>>n>>m;
int tm=m;
for(int i=1;i<=n;++i) cin>>a[i].x,a[i].y=i;
sort(a+1,a+1+n);
reverse(a+1,a+1+n);
for(int i=1;i<=n;++i) sum[i]=sum[i-1]+a[i].x;
memset(f,0x3f,sizeof f);
f[0][0]=0;
for(int i=1;i<=n;++i){
for(int j=1;j<=m;++j){
if(j<i) continue;
f[i][j]=f[i][j-i]; //0个1
for(int k=1;k<=i;++k){
f[i][j]=min(f[i][j],f[i-k][j-k]+(i-k)*(sum[i]-sum[i-k]));
}
}
}
cout<<f[n][m]<<endl;
int i=n,j=m,h=0;
while(i){
if(j>=i&&f[i][j]==f[i][j-i]) j-=i,h++;
else {
for(int k=1;k<=i&&k<=j;++k){
if(f[i][j]==f[i-k][j-k]+(i-k)*(sum[i]-sum[i-k])){
for(int l=i-k+1;l<=i;++l)
ans[a[l].y]=h+1;
i-=k;j-=k;
break;
}
}
}
}
for(int i=1;i<=n;++i) cout<<ans[i]<<" ";
return 0;
}