一, 简介
Finite State Transducers 简称 FST, 中文名:有穷状态转换器。在自然语言处理等领域有很大应用,其功能类似于字典的功能(STL 中的map,C# 中的Dictionary),但其查找是O(1)的,仅仅等于所查找的key长度。目前Lucene4.0在查找Term时就用到了该算法来确定此Term在字典中的位置。
FST 可以表示成FST<Key, Value>的形式,我们可以用O(length(key))的复杂度,找到key所对应的值。除此之外,FST 还支持用Value来查找key以及查找Value最优的key等功能。
FST 如此强大,但是目前网上对其讲解的资料很少,中文的就更是微乎其微了。
二,数据结构
FST 是一种类似于Trie或自动机的数据结构,所以在学习之前您一定要对自动机有一个简单的了解,鉴于篇幅,自动机的内容本文不做介绍。
在查找最优的Value时,会用到求最短路径的Dijikstra算法,但建图过程于此无关。
三,创建FST
为了让大家对FST有一个初步的认识,我们举一个简单的例子来进行说明。
我们假设创建一组映射:Key → Value
“cat” - > 5,
“deep” - > 10,
“do” - > 15
“dog” - > 2,
“dogs” - > 8,
对于经典FST算法来说,要求Key必须按字典序从小到大加入到FST中,原因主要是因为在处理大数据的情况下,我们不太可能把整个FST数据结构都同时放在内存中,而是要边建图边将建好的图存储在外部文件中,以便节省内存。所以我们第一步要对所有的Key排序,对于我给这个例子来说,已经保证了字典序的顺序。
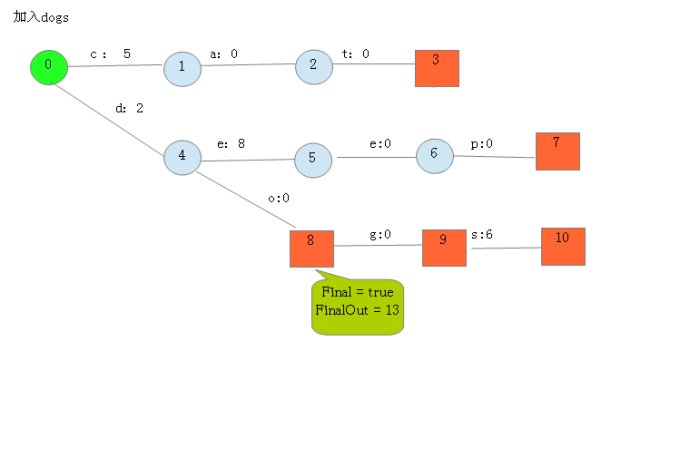
根据此例子的输入我们可以建立下图所示的FST:
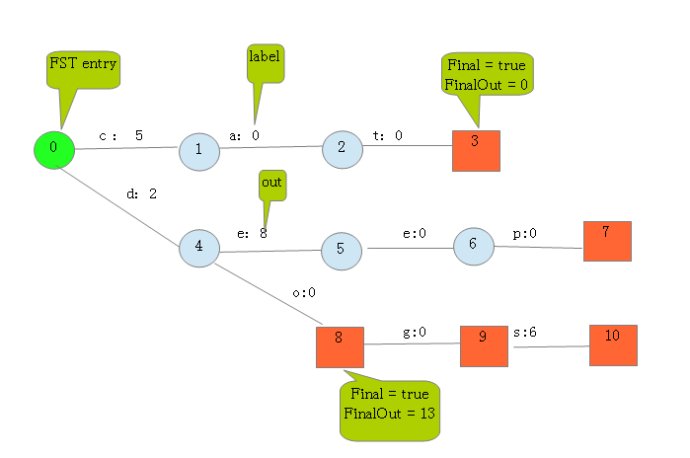
从上图可以看出,每条边有两条属性,一个表示label(key的元素),另一个表示Value(out)。注意Value不一定是数字,还可一是另一个字符串,但要求Value必须满足叠加性,如这里的正整数2 + 8 = 10。字符串的叠加行为: aa + b = aab。
建完这个图之后,我们就可以很容易的查找出任意一个key的Value了。例如:查找dog,我们查找的路径为:0 → 4 → 8 → 9。 其权值和为: 2 + 0 + 0 + 0 = 2。其中最后一个零表示 node[9].finalOut = 0。所以“dog”的Value为2。
到这里,我们已经对FST有了一个感性的认识,下面我们详细讨论FST的建图过程:
1,建一个空节点,表示FST的入口,所有的Key都从这个入口开始。
2, 如果还有未处理的Key,则枚举Key的每一个label。
处理流程如下:
如果当前节点存在含此label的边,则
如果Value包含该边的out值,则
Value = Value – out
否则
令temp=out–Value;
out =Value并使下一个节点的所有边out都加上temp。
如果下一节点是Final节点 则FinalOut += temp
进入下一个节点
否则: 新建一个节点另其out = Value, Value = 0。
如果你看不懂,没关系,我们将用例子演示一遍概算法:
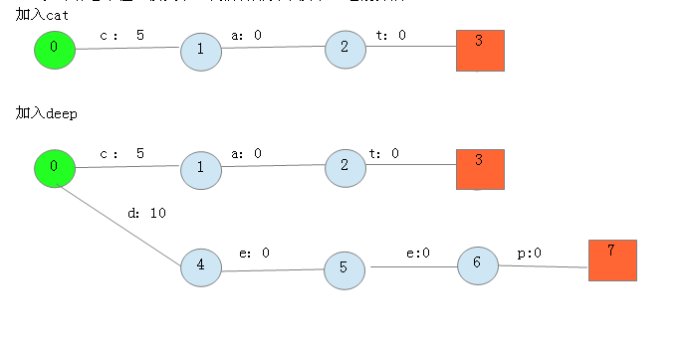
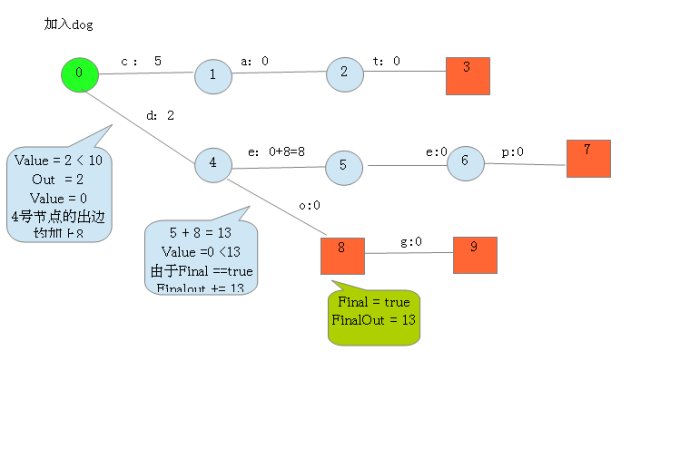
四, 存储FST
通过上面的算法我们看到,FST 本身并不要求输入要按照字典序从小到大,但正如我文章开头说的那样,FST只是一个映射,只能成为我们应用程序的一个工具,所以决不能让这个工具占用我们过多宝贵的内存空间,因此我们要把不用的节点存入到文件中。但是我们的问题是什么样的节点才是不要的节点呢,要解决这个问题还得回顾我们刚才的算法流程。
我们发现存储cat字符串的三个节点自从开始处理deep后就在也没用到过,这是巧合么?如果这是个巧合,那么当开始处理do后就再也没用到过存储eep的三个节点,这是巧合么?如果不是巧合,那到底是什么原因呢?很明显是字典序在做怪!!
正因为,我们保证了所有的Key都是按照字典序加进来的,所以当加入一个新Key的时侯,我们可以先求出新加的Key和上一次输入的Key的公共前缀,然后就可以把 上一次输入的Key除去公共前缀剩下的部分存入文件中了。
综上,可知FST是强大的,但内存是有限的,导致我们必须保证输入有序。
五,应用
尽管FST足够强大,但是在应用过程中,我们仍然可以对其进行再优化,自然语言处理我不太了解,所以不太清楚要如何使用FST来处理自然语言,但是我接触最多的FST的应用就是Lucene。FST在Lucene4.0以后的版本中用于快速定位所查单词在字典中的位置即FST<IntsRef,byteSequence>,由于Lucene是以二进制存储的,所以byteSecquence相当于一个数值,即用多个byte去表示一个数。在Lucene中允许用户设置两个整数minCount1,和minCount2,同时每一个节点记录经过自己的单词数c。
如果c < minCount1 则不存储该节点,因为在大量的文档中,以当前单词为前缀的单词数很少则没有存储的必要,以节省空间。
如果该节点的父节点所经过的单词数pc < minCount2 则删除该节点,原因和上面一样。一般minCount2 >= minCount1。
同时Lucene尽量缩减存储一个节点所需要的空间,比如状态压缩方法。
六,总结
由于网上资料少,自己英语又戳,所以花废了整整一天的时间慢慢啃代码才把此算法弄清楚,鉴于本人时间较紧,所以没有附上自己的程序,如果想了解请查看Lucene4.0官方开源代码Builder.java 的add 方法。目前Lucene还支持FST的反映射,即通过Value找Key,以及前k小的Key(按照Value大小排序)。其实就是在FST上用Dijikstra求最短路。