改改Python代码,运行速度还能提升6万倍,Science:先别想摩尔定律了
如果摩尔定律注定终结,人类的算力会被「锁死」吗?MIT、英伟达、微软研究者合著的一篇 Science 论文告诉我们:不会。
这份最新研究指出,在后摩尔定律时代,人类所获得的的算力提升将更大程度上来源于计算堆栈的「顶层」,即软件、算法和硬件架构,这将成为一个新的历史趋势。
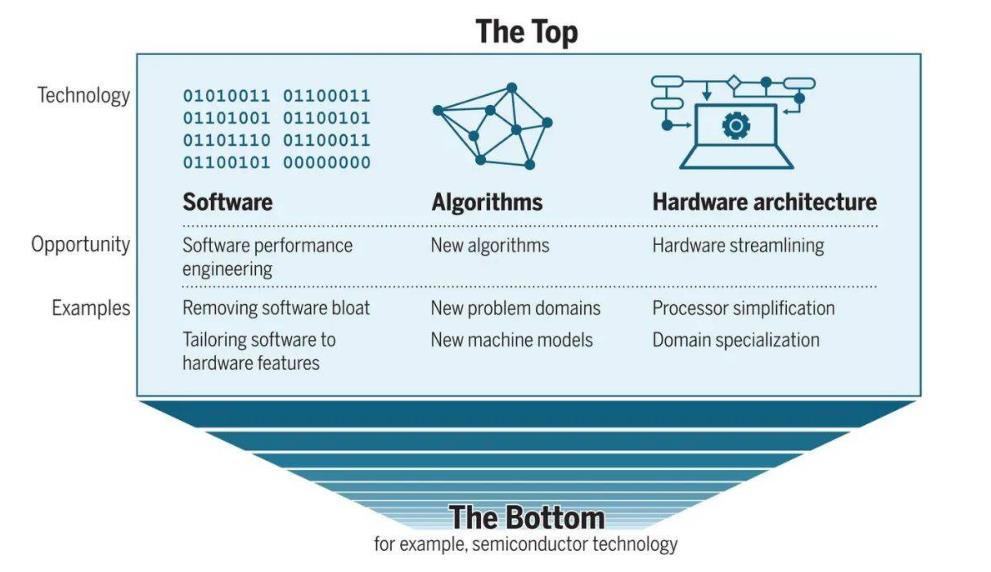
摩尔定律终结之后的性能提升途径。
算力的提升可以为现代生活带来诸多便利,例如,当前手机的功能比 25 年前房间大小的计算机都要强大,近一半的人可以上网,强大的超级计算机还可以用于药物挖掘。人类社会已经了开始依赖计算机随时间指数增长的强大性能了。
计算机性能的提高大部分要归功于数十年来计算机部件的小型化。诺贝尔物理学奖获得者理查德 · 费曼早就预见了这一点。在 1959 年致美国物理学会的演讲中,他提到,「底部还有大量空间」。1975 年,英特尔创始人戈登 · 摩尔给出了这种部件小型化趋势的预测,即集成电路上可容纳的元器件数目约每隔 18-24 个月便会增加一倍,性能也将提升一倍。我们将其称之为摩尔定律。
不幸的是,这种趋势正在走向消亡,因为「底部」已经没有多少空间了。如果算力的提升停滞不前,那么几乎所有行业的生产力都将面临挑战。
在此背景下,MIT、英伟达、微软的研究者在最新一期《Science》上发文指出,虽然「底部」已经没有太多提升的空间,但「顶部」还有机会:在软件、算法以及硬件架构方面,我们都能够找到提升计算性能的方法。
论文链接:https://science.sciencemag.org/content/368/6495/eaam9744
软件
我们可以通过性能工程(performance engineering)把软件做得更加高效,即通过重构软件加快其运行速度。性能工程能够消除程序中的效率低下问题,这种问题被称为软件膨胀(software bloat),是由传统软件的开发策略造成的,即尽可能缩短软件开发时间而不是缩短软件运行时间。性能工程还可以根据运行的硬件来定制软件,如利用并行处理器和矢量单元。
为了说明性能工程的潜在收益,我们思考一个简单的问题:将两个 4096×4096 的矩阵相乘。首先用 Python 代码实现,代码在一台现代计算机上做该矩阵乘法需要 7 个小时,如表 1 中的第一行(Version 1)所示,仅达到机器峰值性能的 0.0006%。
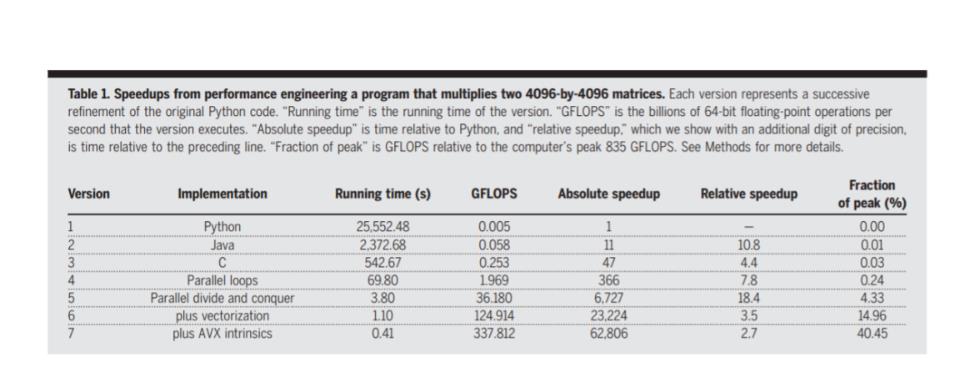
但是,用 Java 实现的代码(Version 2)速度可以提高到原来的 10.8 倍,用 C 语言(Version 3)又可以提升到 Java 的 4.4 倍,运行时间比最初的 Python 版本快 47 倍。这种性能的提升来源于程序运行时操作数量的减少。
此外,根据硬件的特点来调整矩阵乘法的代码甚至可以让运行速度提升 1300 倍。这样的收益是来源于在 18 个处理内核上并行运行代码(Version 4),利用处理器的存储层次结构(Version 5),矢量化代码(Version 6)以及使用英特尔的高级矢量扩展指令集(AVX)(Version 7)。最终,代码优化的方法可以把这项任务所需的时间减少到 0.41 秒——跟需要 7 个小时运行的 Python 相比速度提升了 6 万倍!
值得一提的是,用 Python 3 做同样的事还要更慢,需要耗费 9 个小时。
算法
算法能够为解决问题提供更有效的方法。实际上,自 20 世纪 70 年代末以来,算法在解决最大流问题上的速度提升几乎和硬件带来的加速一样多。但是,在已有的算法问题上的进展是不均匀的和零散的,最终必将面临收益递减的情况。因此,目前最大收益常常来源于新问题领域的算法(例如机器学习)以及开发能更好地反映新兴硬件的新理论机器模型。
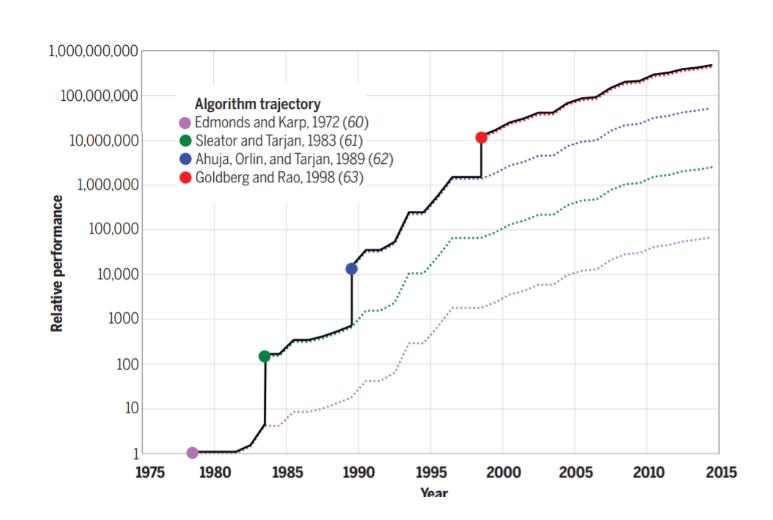
图 1:在求解顶点数 n=10^12,边数 m=10^1.1 的图形的最大流问题上的主要算法进展。
图 1 展示了最大流算法随时间的进展。在 38 年的数据中,最佳算法的性能收益可与摩尔定律所带来的收益相媲美,尽管过去 20 年,在该问题上并没有提升性能的新算法出现。该例子重点介绍了有关算法的 3 个重要观测结果:
1、在已有算法上的改进是不均匀的,而且具有偶然性;
2、算法创新得到的收益可以和摩尔定律相媲美;
3、解决任何已有的问题的算法改进最后都会进展趋缓。
尽管对于已有问题的研究仍能获得少量收益,但是算法上的大量进展将来自于以下 3 个方面:
1、进军新的问题领域;
2、解决可扩展性问题;
3、定制算法以利用当前硬件。
硬件架构
在讨论硬件架构之前,我们先来谈谈「Dennard 缩放比例定律」。
Dennard 缩放比例定律是一个鲜为人知但同样重要的观察结果,Robert Dennard 在 1974 年提出,随着晶体管变得越来越小,它们的功率密度保持不变,因此功率的使用与面积成比例;电压和电流的规模与长度成比例。
结合「摩尔定律」晶体管的数量大约每两年翻一番,这意味着效能功耗比(每消耗一瓦功率,计算机可提供的计算速率)以同样的速度增长,大约每两年翻一番。
Dennard 缩放比例定律在提出之后的 30 年后结束,原因并不是因为晶体管的尺寸不再缩小,而是因为电流和电压不能在继续下降的同时保持可靠性了。随后「多核时代」就到来了。
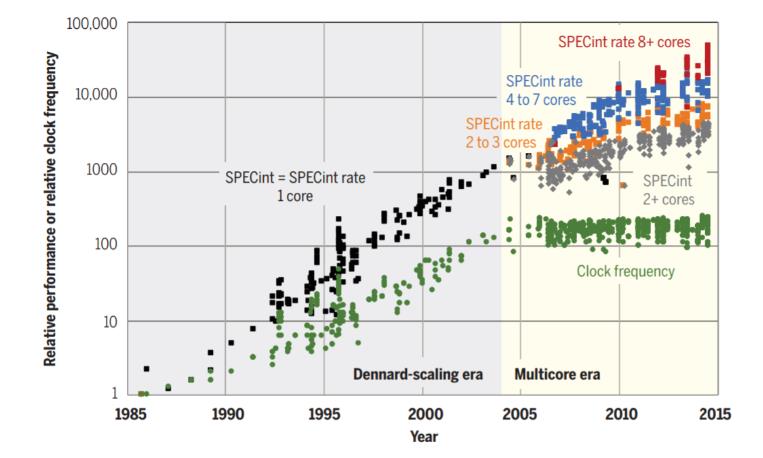
图 2:1985 年 - 2015 年,SPECint 性能(串行为主)、SPECint-rate 性能(并行)、微处理器时钟频率提升的情况。坐标起点为 1985 年的 Intel 80386 DX 微处理器。
上图 2 展示了微处理器的三组基准数据:首先,如图中绿点所示,从 1985 年到 2005 年,由于 Dennard 缩放比例定律的终结,时钟速度在增长了 200 倍之后趋于平缓。
在 Dennard 缩放比例定律时代,由于时钟速度提高和其他架构变化的推动,微处理器在 SPECint 和 SPECintrate 基准测试中的性能迅速提高,目的是在典型的用户工作负载上对计算机性能建模。
SPECint 基准主要由串行代码组成,SPECint-rate 基准测试则是并行的。这两个基准测试在单处理器计算机上的表现是相同的。但从 2004 年之后,由于机器添加了多个内核以及其他的显式并行机制,两者的性能出现差异。
实际上,从 2004 年到 2015 年,性能最佳的芯片上并行应用程序的性能增长了 30 倍,大概每两年就会翻一番。相比之下,同期的 SPECint 基准(灰点)仅增加了三倍。
既然设计者已经接受了并行性,主要问题就是如何简化处理器和利用应用程序的并行性。未来,两种简化策略将占据主导地位:处理器简化和领域专门化。
硬件架构是可简化的。一种是通过简化处理器,将复杂的处理核替换为晶体管数量需求更少的简单处理核。由此释放出的晶体管预算可重新分配到其他用途上,比如增加并行运行的处理核的数量,这将大幅提升可利用并行性问题的效率。
简化的另一种形式是领域专门化(domain specialization),即针对特定应用程序定制硬件。这种专门化舍弃了某一领域不需要的处理功能,同时允许针对领域进行更多的自定义,比如降低机器学习应用程序的浮点精度。
在后摩尔时代,软件、算法和硬件体系架构的性能改进越来越依靠在堆栈的各个级别上进行并发更改。从工程管理和经济的角度看,这类更改在大型系统组件中更容易实现,因为这些可重用的软件通常具有超过一百万行的代码,或者是拥有相当复杂的硬件。
如果一个组织和公司拥有此类的大型组件,通过重新设计模块度来获得性能提升是比较容易的。此外,成本和收益可以合在一起考虑,这样一来,大型组件中某一部分重要但昂贵的更改就能用该组件中其他部分的收益来弥补。
「底层」或许还有机会
在后摩尔时代,处于「底层」的制硅工艺改进将不再提供那么显著的计算机性能提升,但「顶层」的软件性能更迭、算法开发和硬件精简,将使计算机应用程序的速度更快。与曾经「底层」明显的收益不同,这些「顶层」的收益将会是参差不齐、零散且机会性的。而且,随着对特定计算方法的探索不断深入,这种边际收益将会呈现递减趋势。
当然,一些新兴技术也可能从「底层」推动发展,比如 3D 堆叠、量子计算、光子学、超导电路、神经形态计算、石墨烯芯片。这些技术目前还处于起步阶段,尚未成熟,暂时无法与基于硅的半导体技术竞争。但不可否认的是,它们的确具备长期潜力。