// 此博文为迁移而来,写于2015年5月12日,不代表本人现在的观点与看法。原始地址:http://blog.sina.com.cn/s/blog_6022c4720102w03t.html
UPDATE(20190304):进行一些修正。
UPDATE(20180822):重写代码。
1、前言
线段树,众所周知,在树中的每一个元素中,保存的是线段中的一段,所维护的内容或是最大最小值,或是和等等。可持久化线段树,属于可持久化数据结构中的一种,对于可持久化数据结构这个大知识,我暂时没有去研究,今天只讲其冰山一角。
2、概念
可持久化,表示我们当前在处理每个状态,而之前的状态即状态的历史版本全部能够存下来。可持久化线段树,实质上是多颗线段树,最简单的可持久化线段树的题目:求区间第k大。显而易见,求区间最大值的时候我们用普通的线段树就行了,第k大总不能一个个从1数到k吧?可持久化的结构在这个时候就能够帮上大忙了。
我们设区间有n个元素,然后依次进行读入。每读入一个数字,都需要新建一颗线段树(后面会有扩展),这就是能够保存历史状态的线段树了。线段树中每一个节点维护的是当前已经输入的数的数值位于该区间的个数。有点绕口,没错此时此刻的我也才刚刚懂了——说的直白一点,设目前是第n棵线段树中有一个节点为[1,4],表示前n个数中数值在1至4的数的个数。
可持久化线段树还有另一个名字——主席树。
3、离散化
但依旧存在一个问题,题目的空间限制肯定是有的,假设所输入的数的范围为int,开一个int大小的树显然不现实,而且还要多棵线段树。此时此刻,我们需要用到离散化。看起来很高端,其实很简单,脑补一下C++中的Map(STL)就行了,或者回忆一下高中数学必修一集合那一章,有一个叫映射的东西,和离散化意思差不多(起码在这道题上的作用是一模一样的),所以不详细阐述,在源代码中会有小小的注释。
好了,目前有一个数列:{2,8,19,6}。假设我们已经离散化结束了,结果为2→1;6→2;8→3;19→4。那么以后我们进行数据的处理时,1就表示2了,2就表示6了,3就表示8了。。。是不是和映射一个意思?
这样的好处在于,我们不需要依赖就弄个[1,2147483647]的线段树了,若题目规定n<=100000,则最大只需要一棵[1,10000]的线段树了。如下图(其实没有蛮多含义,真正的变化在后面):

【若是建一棵[1,19]的线段树是多么浪费空间】
4、历史版本的作用
这么多棵线段树,我们也不可能建立多个结构体来保存。我们可以把所有线段树的节点全部放在tree结构体中,设当前有m个节点,每执行一次插入操作,新增了x个节点,则存放在tree中的第(m+1)个节点至第(m+x)个节点(当然也有别的编号方式)。同时,我们需要一个root数组,其中root[i]表示第i棵线段树的根节点的编号。
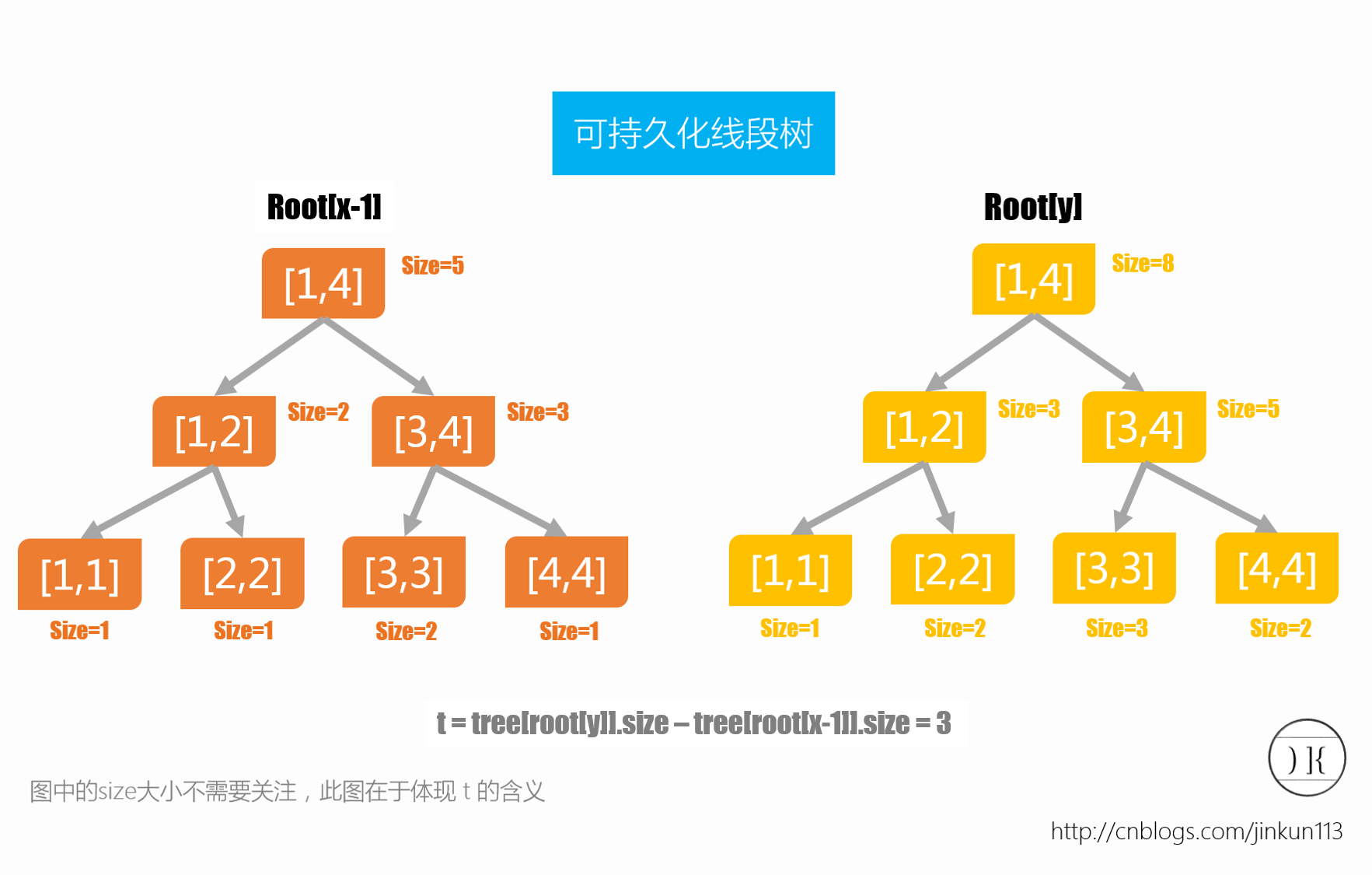
这样我们就构建完了,来想想——为什么需要历史版本?回到我们一开始的问题,求区间第k大,假设当前询问为求[x,y]的第k大,则我们所需要用到的线段树为第x+1棵到第y棵。
从根节点开始,我们将第y棵树和第x+1棵树一一对应的节点所维护的值进行相减,其所得到的数就是在所询问的[x,y]中,当前节点表示的子区间的那几个数值在整个区间中出现的次数,首先令t=root[y].[1,mid]-root[x-1].[1,mid],即根节点的左儿子。
若t>=k,则说明在区间中至少存在[1,mid]的数的个数大于k,则向右儿子递归查询,因为第k大必定在[mid+1,r]之中了;反之,若t<k,则必定在[1,mid]中,即向左儿子递归查询。
5、缩小空间
其实必要的知识已经讲得差不多了,但是我们最后还要面临一个问题——加入一个数,就新建一棵线段树。我们假设有100000个数吧,且有100000次询问,试想这一大片庞大的线段树森林是要占用多大的内存?一定会MLE的(当然数据小就无所谓)。
我们有什么办法缩小空间需求?我们注意到,每次我们加入一个被离散化后的数x,则从根结点开始向下更新,我们真正相对于前面一棵线段树的差异之处是很少的!设有一颗[1,4]的线段树,若当前插入值为3,则[1,4]的左儿子[1,2]没有丝毫改动!如果又新建一个,完全是浪费。
这样子,我们就有一个方法缩小冗余的空间了——将没有区别的部分直接指回去,如图所示:

由于所有的线段树在同一个结构体之中,我们将其指向以前存在的节点是非常轻松的。这样,空间会节省很多。
6、例题
如前面所说,求区间第k小。【HDU 2665】
题目描述
Give you a sequence and ask you the kth big number of a inteval.(英文题面感觉有一定歧义……)
输入格式
The first line is the number of the test cases.
For each test case, the first line contain two integer n and m (n, m <= 100000), indicates the number of integers in the sequence and the number of the quaere.
The second line contains n integers, describe the sequence.
Each of following m lines contains three integers s, t, k.
[s, t] indicates the interval and k indicates the kth big number in interval [s, t]
输出格式
For each test case, output m lines. Each line contains the kth big number.
输入样例
1
10 1
1 4 2 3 5 6 7 8 9 0
1 3 2
输出样例
2
代码:
#include <cstdio> #include <algorithm> using namespace std; #define MAXN 100005 int T, n, m, l, r, k, tot, root[MAXN], b[MAXN], lik[MAXN]; struct num { int w, n, r; } a[MAXN]; struct cmpw { bool operator () (num a, num b) { return a.w < b.w; } } cw; struct cmpn { bool operator () (num a, num b) { return a.n < b.n; } } cn; struct Tree { int l, r, w; } t[MAXN * 20]; void chg() { sort(a + 1, a + n + 1, cw); for (int i = 1; i <= n; i++) a[i].r = i; sort(a + 1, a + n + 1, cn); for (int i = 1; i <= n; i++) b[i] = a[i].r, lik[b[i]] = a[i].w; } void build(int o, int l, int r, int w, int x) { t[o] = t[x], t[o].w++; if (l == r) return; int m = (l + r) >> 1; if (w <= m) build(t[o].l = ++tot, l, m, w, t[x].l); else build(t[o].r = ++tot, m + 1, r, w, t[x].r); } int query(int rl, int rr, int l, int r, int k) { if (l == r) return l; int w = t[t[rr].l].w - t[t[rl].l].w, m = (l + r) >> 1; return w >= k ? query(t[rl].l, t[rr].l, l, m, k) : query(t[rl].r, t[rr].r, m + 1, r, k - w); } int main() { scanf("%d", &T); for (int j = 1; j <= T; j++) { root[0] = 0, tot = 0; scanf("%d %d", &n, &m); for (int i = 1; i <= n; i++) scanf("%d", &a[i].w), a[i].n = i; chg(); for (int i = 1; i <= n; i++) build(root[i] = ++tot, 1, n, b[i], root[i - 1]); for (int i = 1; i <= m; i++) { scanf("%d %d %d", &l, &r, &k); printf("%d ", lik[query(root[l - 1], root[r], 1, n, k)]); } } return 0; }