http://blog.csdn.net/v1_vivian/article/details/52055760
上篇博文中,我们知道了指数分布族,它的定义式为:
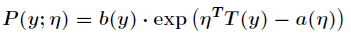 ,
,这次我们要了解的广义线性模型,是基于指数分布族的,我们可以通过指数分布族引出广义线性模型(Generalized LinearModel,GLM)。这种模型是把自变量的线性预测函数当作因变量的估计值。
实际上线性最小二乘回归和Logistic回归都是广义线性模型的一个特例。当随机变量y服从高斯分布,η与正太分布的参数μ的关系是相等,那么得到的是线性最小二乘回归,当随机变量y服从伯努利分布,η与参数φ的关系是logistic函数,我们得到logistic回归。
由此可以看出,η以不同的映射函数与其它概率分布函数中的参数发生联系,从而得到不同的模型,广义线性模型正式将指数分布族中的所有成员(每个成员正好有一个这样的联系)都作为线性模型的扩展,通过各种非线性的连接函数将线性函数映射到其它空间从而大大扩大了线性模型可解决的问题。
如何根据指数分布族来构建广义线性模型?
GLM以三个假设为前提:
(1)给定特征属性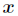 和参数
和参数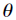 后,
后, 的条件概率
的条件概率 服从指数分布族,即
服从指数分布族,即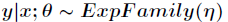
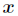 和参数
和参数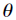 后,
后, 的条件概率
的条件概率 服从指数分布族,即
服从指数分布族,即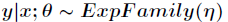
(2)给定一个x,预测T(y)的期望值为:

(3)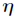 与
与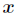 之间是线性的,即
之间是线性的,即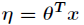 。
。
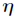 与
与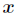 之间是线性的,即
之间是线性的,即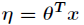 。
。依据这三个假设,我们可以推导出logistic模型与最小二乘模型。
对于最小二乘模型,推导过程如下:


Logistic模型的推导过程如下:
其中,将η与原始概率分布中的参数联系起来的函数称为正则响应函数(canonical response function),如
正则响应函数的逆称为正则关联函数(canonical link function)。
所以,对于广义线性模型,需要决策的是选用什么样的分布,当选取高斯分布时,我们就得到最小二乘模型,当选取伯努利分布时,我们得到logistic模型,这里所说的模型是假设函数h的形式。
总结一下,广义线性模型通过假设一个概率分布,得到不同的模型,而之前所讨论的梯度下降,牛顿方法都是为了求取模型中的线性部分 的参数θ。
的参数θ。
 的参数θ。
的参数θ。
