【转载】用OCTAVE实现一元线性回归的梯度下降算法

原文地址：http://www.cnblogs.com/KID-XiaoYuan/p/7247481.html

STEP1 PLOTTING THE DATA

在处理数据之前，我们通常要了解数据，对于这次的数据集合，我们可以通过离散的点来描绘它，在一个2D的平面里把它画出来。

 

我们把ex1data1中的内容读取到X变量和y变量中，用m表示数据长度。

1 2 3 4

data = load('ex1data1.txt'); X = data(:,1); y = data(:,2); m = length(y);

接下来通过图像描绘出来。

1 2 3

plot(x,y,'rx','MakerSize',10); ylabel('Profit in $10,000s'); xlabel('Population of City in 10,000s');

　　现在我们得到图像如图所示，就是原始的数据的直观表示。

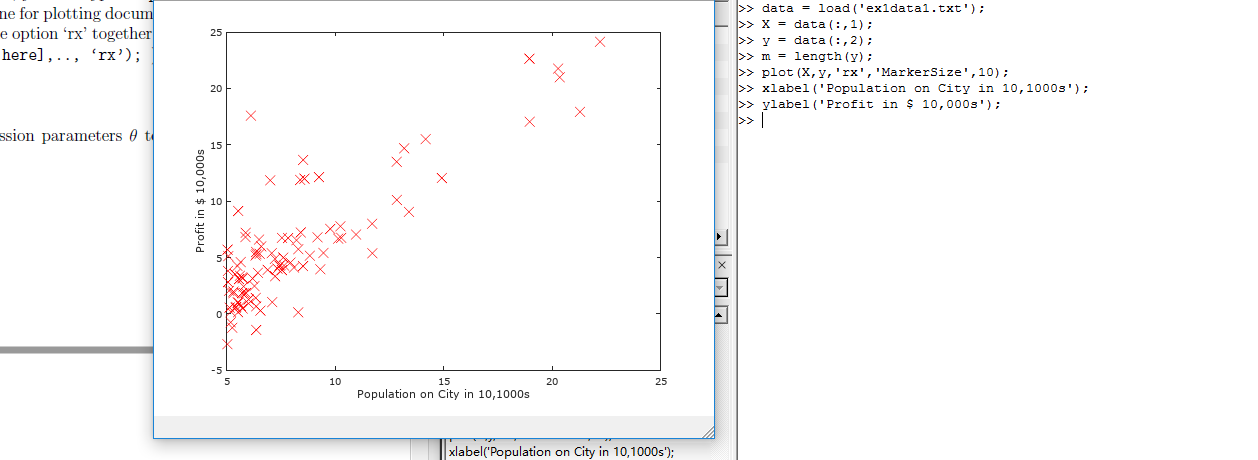
STEP2 GRADIENT DESCENT

现在，我们通过梯度下降法对参数θ进行线性回归。

依照我们之前所得出步骤方法

迭代更新

计算θ值函数：

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23

function J = computeCost(X, y, theta) %COMPUTECOST Compute cost for linear regression %   J = COMPUTECOST(X, y, theta) computes the cost of using theta as the %   parameter for linear regression to fit the data points in X and y   % Initialize some useful values m = length(y); % number of training examples   % You need to return the following variables correctly J = 0;   % ====================== YOUR CODE HERE ====================== % Instructions: Compute the cost of a particular choice of theta %               You should set J to the cost. J = sum((X * theta - y).^2) / (2*m);     % X(79,2)  theta(2,1)           % =========================================================================   end

　　接下来是梯度下降函数

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33

function [theta, J_history] = gradientDescent(X, y, theta, alpha, num_iters) %GRADIENTDESCENT Performs gradient descent to learn theta %   theta = GRADIENTDESENT(X, y, theta, alpha, num_iters) updates theta by %   taking num_iters gradient steps with learning rate alpha   % Initialize some useful values m = length(y); % number of training examples J_history = zeros(num_iters, 1); theta_s=theta;   for iter = 1:num_iters       % ====================== YOUR CODE HERE ======================     % Instructions: Perform a single gradient step on the parameter vector     %               theta.     %     % Hint: While debugging, it can be useful to print out the values     %       of the cost function (computeCost) and gradient here.     %     theta(1) = theta(1) - alpha / m * sum(X * theta_s - y);           theta(2) = theta(2) - alpha / m * sum((X * theta_s - y) .* X(:,2));     % 必须同时更新theta(1)和theta(2)，所以不能用X * theta,而要用theta_s存储上次结果。     theta_s=theta;             % ============================================================       % Save the cost J in every iteration        J_history(iter) = computeCost(X, y, theta);   end J_history end

绘图函数：

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28

function plotData(x, y) %PLOTDATA Plots the data points x and y into a new figure % PLOTDATA(x,y) plots the data points and gives the figure axes labels of % population and profit.   % ====================== YOUR CODE HERE ====================== % Instructions: Plot the training data into a figure using the % "figure" and "plot" commands. Set the axes labels using % the "xlabel" and "ylabel" commands. Assume the % population and revenue data have been passed in % as the x and y arguments of this function. % % Hint: You can use the 'rx' option with plot to have the markers % appear as red crosses. Furthermore, you can make the % markers larger by using plot(..., 'rx', 'MarkerSize', 10);   figure; % open a new figure window plot(x, y, 'rx', 'MarkerSize', 10); % Plot the data ylabel('Profit in $10,000s'); % Set the y axis label xlabel('Population of City in 10,000s'); % Set the x axis label             % ============================================================   end

　　　　根据以上函数，我们进行线性回归：

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120

<br>%% Machine Learning Online Class - Exercise 1: Linear Regression   %  Instructions %  ------------ % %  This file contains code that helps you get started on the %  linear exercise. You will need to complete the following functions %  in this exericse: % %     warmUpExercise.m %     plotData.m %     gradientDescent.m %     computeCost.m %     gradientDescentMulti.m %     computeCostMulti.m %     featureNormalize.m %     normalEqn.m % %  For this exercise, you will not need to change any code in this file, %  or any other files other than those mentioned above. % % x refers to the population size in 10,000s % y refers to the profit in $10,000s %     %% ==================== Part 1: Basic Function ==================== % Complete warmUpExercise.m fprintf('Running warmUpExercise ... '); fprintf('5x5 Identity Matrix: '); warmUpExercise()   fprintf('Program paused. Press enter to continue. '); pause;     %% ======================= Part 2: Plotting ======================= fprintf('Plotting Data ... ') data = load('ex1data1.txt'); X = data(:, 1); y = data(:, 2); m = length(y); % number of training examples   % Plot Data % Note: You have to complete the code in plotData.m plotData(X, y);   fprintf('Program paused. Press enter to continue. '); pause;   %% =================== Part 3: Gradient descent =================== fprintf('Running Gradient Descent ... ')   X = [ones(m, 1), data(:,1)]; % Add a column of ones to x theta = zeros(2, 1); % initialize fitting parameters   % Some gradient descent settings iterations = 1500; alpha = 0.01;   % compute and display initial cost computeCost(X, y, theta)   % run gradient descent theta = gradientDescent(X, y, theta, alpha, iterations);   % print theta to screen fprintf('Theta found by gradient descent: '); fprintf('%f %f ', theta(1), theta(2));   % Plot the linear fit hold on; % keep previous plot visible plot(X(:,2), X*theta, '-') legend('Training data', 'Linear regression') hold off % don't overlay any more plots on this figure   % Predict values for population sizes of 35,000 and 70,000 predict1 = [1, 3.5] *theta; fprintf('For population = 35,000, we predict a profit of %f ',...     predict1*10000); predict2 = [1, 7] * theta; fprintf('For population = 70,000, we predict a profit of %f ',...     predict2*10000);   fprintf('Program paused. Press enter to continue. '); pause;   %% ============= Part 4: Visualizing J(theta_0, theta_1) ============= fprintf('Visualizing J(theta_0, theta_1) ... ')   % Grid over which we will calculate J theta0_vals = linspace(-10, 10, 100); theta1_vals = linspace(-1, 4, 100);   % initialize J_vals to a matrix of 0's J_vals = zeros(length(theta0_vals), length(theta1_vals));   % Fill out J_vals for i = 1:length(theta0_vals)     for j = 1:length(theta1_vals)       t = [theta0_vals(i); theta1_vals(j)];          J_vals(i,j) = computeCost(X, y, t);     end end     % Because of the way meshgrids work in the surf command, we need to % transpose J_vals before calling surf, or else the axes will be flipped J_vals = J_vals'; % Surface plot figure; surf(theta0_vals, theta1_vals, J_vals) xlabel(' heta_0'); ylabel(' heta_1');   % Contour plot figure; % Plot J_vals as 15 contours spaced logarithmically between 0.01 and 100 contour(theta0_vals, theta1_vals, J_vals, logspace(-2, 3, 20)) xlabel(' heta_0'); ylabel(' heta_1'); hold on; plot(theta(1), theta(2), 'rx', 'MarkerSize', 10, 'LineWidth', 2);

　　

如图所示，绘制出线性回归函数。

这时所绘制2D等高线图梯度下降表面图：

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 240 241 242 243 244 245 246 247 248 249 250 251 252 253 254 255 256 257 258 259 260 261 262 263 264 265 266 267 268 269 270 271

function [X_norm, mu, sigma] = featureNormalize(X) %FEATURENORMALIZE Normalizes the features in X %   FEATURENORMALIZE(X) returns a normalized version of X where %   the mean value of each feature is 0 and the standard deviation %   is 1. This is often a good preprocessing step to do when %   working with learning algorithms.   % You need to set these values correctly X_norm = X; mu = zeros(1, size(X, 2));      % mean value 均值   size(X,2)  列数 sigma = zeros(1, size(X, 2));   % standard deviation  标准差   % ====================== YOUR CODE HERE ====================== % Instructions: First, for each feature dimension, compute the mean %               of the feature and subtract it from the dataset, %               storing the mean value in mu. Next, compute the %               standard deviation of each feature and divide %               each feature by it's standard deviation, storing %               the standard deviation in sigma. % %               Note that X is a matrix where each column is a %               feature and each row is an example. You need %               to perform the normalization separately for %               each feature. % % Hint: You might find the 'mean' and 'std' functions useful. %         mu = mean(X);       %  mean value   sigma = std(X);     %  standard deviation   X_norm  = (X - repmat(mu,size(X,1),1)) ./  repmat(sigma,size(X,1),1);                  % ============================================================   end function [theta, J_history] = gradientDescentMulti(X, y, theta, alpha, num_iters) %GRADIENTDESCENTMULTI Performs gradient descent to learn theta %   theta = GRADIENTDESCENTMULTI(x, y, theta, alpha, num_iters) updates theta by %   taking num_iters gradient steps with learning rate alpha   % Initialize some useful values m = length(y); % number of training examples J_history = zeros(num_iters, 1);   for iter = 1:num_iters       % ====================== YOUR CODE HERE ======================     % Instructions: Perform a single gradient step on the parameter vector     %               theta.     %     % Hint: While debugging, it can be useful to print out the values     %       of the cost function (computeCostMulti) and gradient here.     %     theta = theta - alpha / m * X' * (X * theta - y);         % ============================================================       % Save the cost J in every iteration        J_history(iter) = computeCostMulti(X, y, theta);   end   end function J = computeCostMulti(X, y, theta) %COMPUTECOSTMULTI Compute cost for linear regression with multiple variables %   J = COMPUTECOSTMULTI(X, y, theta) computes the cost of using theta as the %   parameter for linear regression to fit the data points in X and y   % Initialize some useful values m = length(y); % number of training examples   % You need to return the following variables correctly J = 0;   % ====================== YOUR CODE HERE ====================== % Instructions: Compute the cost of a particular choice of theta %               You should set J to the cost. J = sum((X * theta - y).^2) / (2*m);            % =========================================================================   end function [theta] = normalEqn(X, y) %NORMALEQN Computes the closed-form solution to linear regression %   NORMALEQN(X,y) computes the closed-form solution to linear %   regression using the normal equations.   theta = zeros(size(X, 2), 1);   % ====================== YOUR CODE HERE ====================== % Instructions: Complete the code to compute the closed form solution %               to linear regression and put the result in theta. %   % ---------------------- Sample Solution ----------------------   theta = pinv( X' * X ) * X' * y;     % -------------------------------------------------------------     % ============================================================   end %% Machine Learning Online Class %  Exercise 1: Linear regression with multiple variables % %  Instructions %  ------------ % %  This file contains code that helps you get started on the %  linear regression exercise. % %  You will need to complete the following functions in this %  exericse: % %     warmUpExercise.m %     plotData.m %     gradientDescent.m %     computeCost.m %     gradientDescentMulti.m %     computeCostMulti.m %     featureNormalize.m %     normalEqn.m % %  For this part of the exercise, you will need to change some %  parts of the code below for various experiments (e.g., changing %  learning rates). %   %% Initialization   %% ================ Part 1: Feature Normalization ================   %% Clear and Close Figures clear ; close all; clc   fprintf('Loading data ... ');   %% Load Data data = load('ex1data2.txt'); X = data(:, 1:2); y = data(:, 3); m = length(y);   % Print out some data points fprintf('First 10 examples from the dataset: '); fprintf(' x = [%.0f %.0f], y = %.0f ', [X(1:10,:) y(1:10,:)]');   fprintf('Program paused. Press enter to continue. '); pause;   % Scale features and set them to zero mean fprintf('Normalizing Features ... ');   [X mu sigma] = featureNormalize(X);      % 均值0，标准差1   % Add intercept term to X X = [ones(m, 1) X];     %% ================ Part 2: Gradient Descent ================   % ====================== YOUR CODE HERE ====================== % Instructions: We have provided you with the following starter %               code that runs gradient descent with a particular %               learning rate (alpha). % %               Your task is to first make sure that your functions - %               computeCost and gradientDescent already work with %               this starter code and support multiple variables. % %               After that, try running gradient descent with %               different values of alpha and see which one gives %               you the best result. % %               Finally, you should complete the code at the end %               to predict the price of a 1650 sq-ft, 3 br house. % % Hint: By using the 'hold on' command, you can plot multiple %       graphs on the same figure. % % Hint: At prediction, make sure you do the same feature normalization. %   fprintf('Running gradient descent ... ');   % Choose some alpha value alpha = 0.01; num_iters = 8500;   % Init Theta and Run Gradient Descent theta = zeros(3, 1); [theta, J_history] = gradientDescentMulti(X, y, theta, alpha, num_iters);   % Plot the convergence graph figure; plot(1:numel(J_history), J_history, '-b', 'LineWidth', 2); xlabel('Number of iterations'); ylabel('Cost J');   % Display gradient descent's result fprintf('Theta computed from gradient descent: '); fprintf(' %f ', theta); fprintf(' ');   % Estimate the price of a 1650 sq-ft, 3 br house % ====================== YOUR CODE HERE ====================== % Recall that the first column of X is all-ones. Thus, it does % not need to be normalized. price = [1 (([1650 3]-mu) ./ sigma)] * theta ; % ============================================================   fprintf(['Predicted price of a 1650 sq-ft, 3 br house ' ...          '(using gradient descent): $%f '], price);   fprintf('Program paused. Press enter to continue. '); pause;   %% ================ Part 3: Normal Equations ================   fprintf('Solving with normal equations... ');   % ====================== YOUR CODE HERE ====================== % Instructions: The following code computes the closed form %               solution for linear regression using the normal %               equations. You should complete the code in %               normalEqn.m % %               After doing so, you should complete this code %               to predict the price of a 1650 sq-ft, 3 br house. %   %% Load Data data = csvread('ex1data2.txt'); X = data(:, 1:2); y = data(:, 3); m = length(y);   % Add intercept term to X X = [ones(m, 1) X];   % Calculate the parameters from the normal equation theta = normalEqn(X, y);   % Display normal equation's result fprintf('Theta computed from the normal equations: '); fprintf(' %f ', theta); fprintf(' ');     % Estimate the price of a 1650 sq-ft, 3 br house % ====================== YOUR CODE HERE ====================== price = [1 1650 3] * theta ;     % ============================================================   fprintf(['Predicted price of a 1650 sq-ft, 3 br house ' ...          '(using normal equations): $%f '], price);

　　处理前：

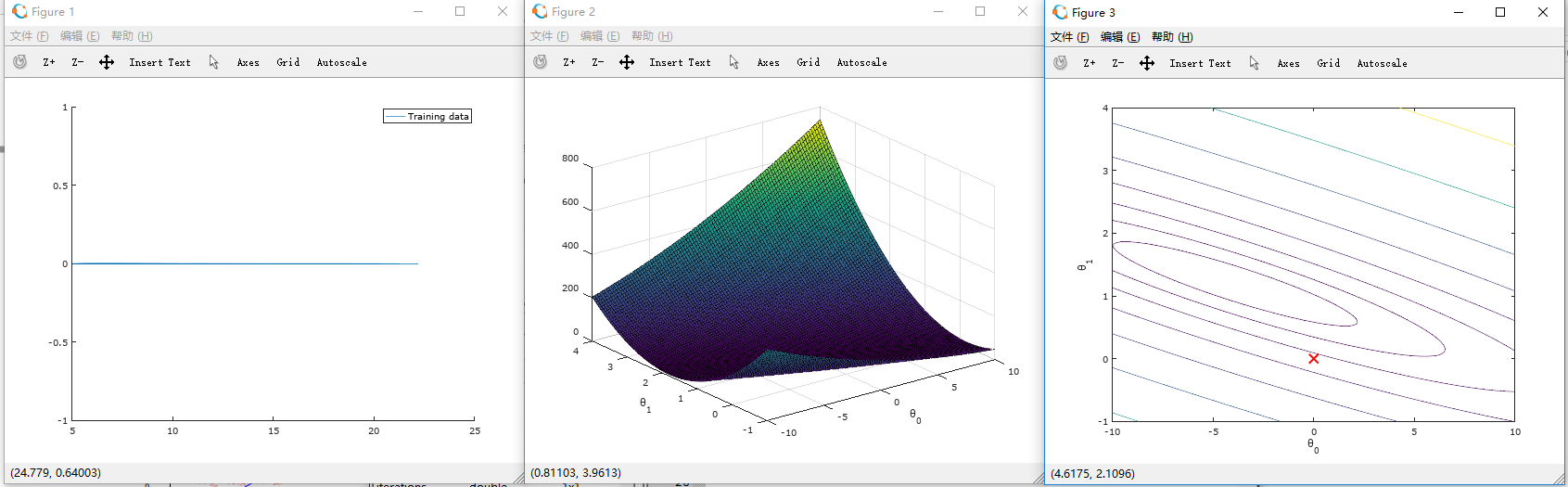
处理后：

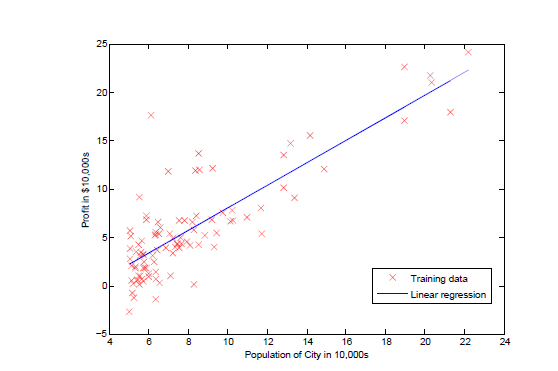
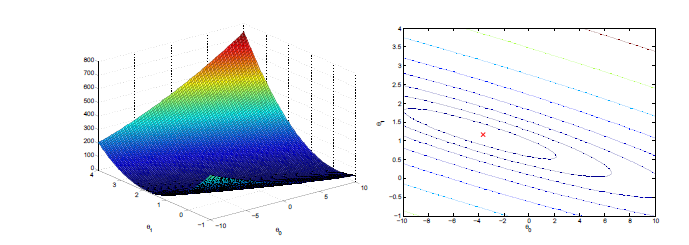
 回归过程如图所示：

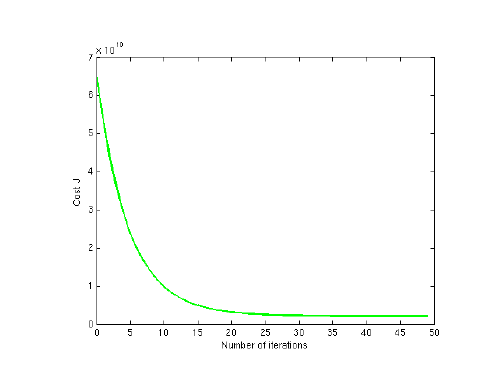
至此，我们通过梯度下降法解决了此问题，我们还可以通过之前所说的数学方法来解决，但是对于数据太大的情况（通常大于10000），我们就会通过梯度下降法来解决了

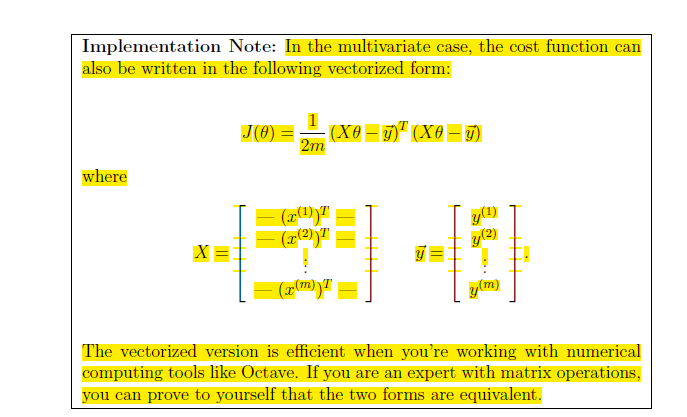
　　根据以上函数，我们进行线性回归：