原文地址:http://www.cnblogs.com/KID-XiaoYuan/p/7011466.html
监督学习
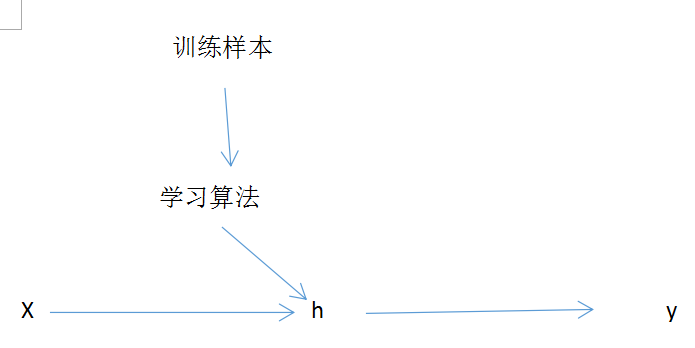
简单来说监督学习模型如图所示
其中 x是输入变量 又叫特征向量 y是输出变量 又叫目标向量
通常的我们用(x,y)表示一个样本 而第i个样本 用(x(i),y(i))表示
h是输出函数
监督学习的任务是学习一个模型,使模型能够对任意的输入,做出很好的预测。
习惯的样本训练数目用m表示
梯度下降算法
h(x) = Θ0 +Θ1x1+...+Θixi
J(Θ)= 1/2 *∑(i from 1 to m) (h(Θ)(x (i) - y(i))^2
Θ(i) := Θ(i) - α * (∂/∂Θ(i))J(Θ)
(其过程好比在山上某一点 在当前点找到最一个方向,使得这点下山速度最快,其原理是通过求导,使梯度下降)
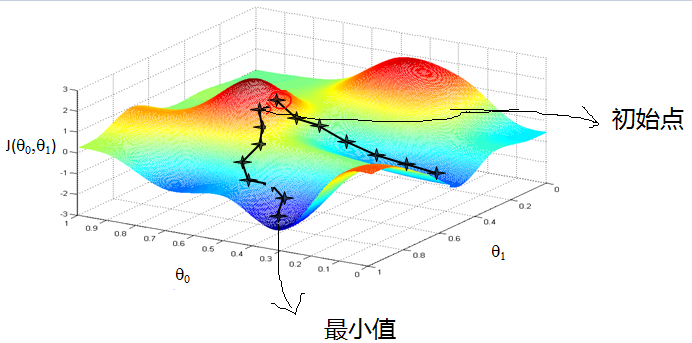
梯度下降算法的计算步骤:
1. 先决条件: 确认优化模型的假设函数和损失函数。
比如对于线性回归,假设函数表示为 hθ(x1,x2,...xn)=θ0+θ1x1+...+θnxn, 其中θi (i = 0,1,2... n)为模型参数,xi (i = 0,1,2... n)为每个样本的n个特征值。这个表示可以简化,我们增加一个特征x0=1 ,这样hθ(x0,x1,...xn)=∑i=0nθixihθ。
同样是线性回归,对应于上面的假设函数,损失函数为:
J(θ0,θ1...,θn)=12m∑i=0m(hθ(x0,x1,...xn)−yi)2J(θ0,θ1...,θn)=12m∑i=0m(hθ(x0,x1,...xn)−yi)2
2. 算法相关参数初始化:主要是初始化θ0,θ1...,θn,算法终止距离ε以及步长α。在没有任何先验知识的时候,我喜欢将所有的θ初始化为0, 将步长初始化为1。在调优的时候再 优化。
3. 算法过程:
1)确定当前位置的损失函数的梯度,对于θiθi,其梯度表达式如下:
∂θiJ(θ0,θ1...,θn)
2)用步长乘以损失函数的梯度,得到当前位置下降的距离,即α∂θiJ(θ0,θ1...,θn)对应于前面登山例子中的某一步。
3)确定是否所有的θi,梯度下降的距离都小于εε,如果小于ε则算法终止,当前所有的θi(i=0,1,...n)即为最终结果。否则进入步骤4.
4)更新所有的θθ,对于θi,其更新表达式如下。更新完毕后继续转入步骤1.
θi:=θi−α∂θiJ(θ0,θ1...,θn)
例如 : 对房屋的现有x1 = 尺寸 x2 = 邻居
则有h(x) = hθ(x) = θ0 +θ1x1+θ2x2 (θ0 = 0)
= ∑ (n from 1 to n) θixi = θTx;
J(θ) = (∂/∂Θ(i))(1/2 * hθ(x) -y)^2;
J'(θ) = [hθ(x) -y)]*x(i);
更新步骤 θ(i) := θ(i) - α (hθ(x) - y)*x(i);
(α为学习速度)
通过不断的迭代更新,减小梯度 直到收敛
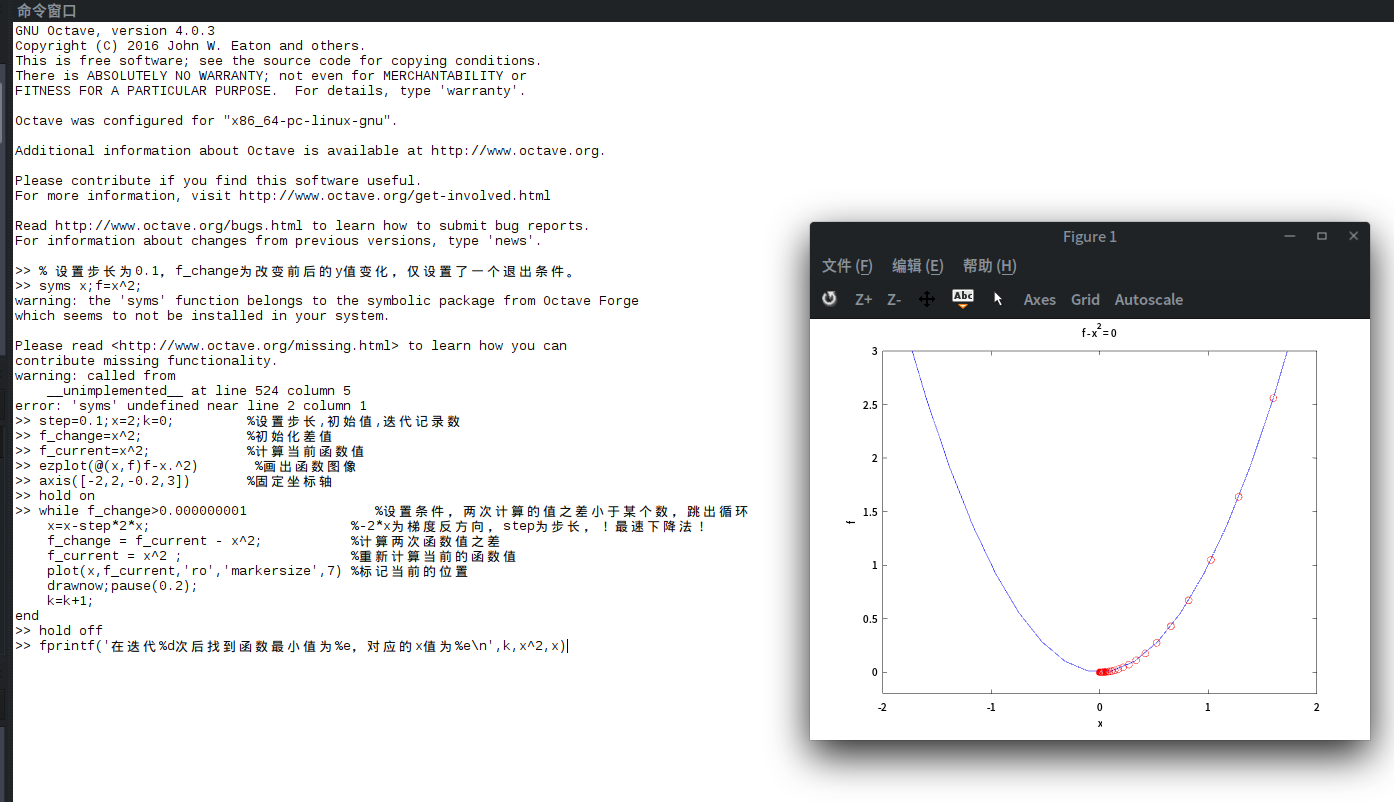
在MATLAB下实现
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
|
% 设置步长为0.1,f_change为改变前后的y值变化,仅设置了一个退出条件。syms x;f=x^2;step=0.1;x=2;k=0; %设置步长,初始值,迭代记录数f_change=x^2; %初始化差值f_current=x^2; %计算当前函数值ezplot(@(x,f)f-x.^2) %画出函数图像axis([-2,2,-0.2,3]) %固定坐标轴hold onwhile f_change>0.000000001 %设置条件,两次计算的值之差小于某个数,跳出循环 x=x-step*2*x; %-2*x为梯度反方向,step为步长,!最速下降法! f_change = f_current - x^2; %计算两次函数值之差 f_current = x^2 ; %重新计算当前的函数值 plot(x,f_current,'ro','markersize',7) %标记当前的位置 drawnow;pause(0.2); k=k+1;endhold offfprintf('在迭代%d次后找到函数最小值为%e,对应的x值为%e
',k,x^2,x) |
|
1
|
运行结果如图所示:(在octave中实现) |