基本思想:
将一个记录插入到已排序好的有序表中,从而得到一个新,记录数增1的有序表。即:先将序列的第1个记录看成是一个有序的子序列,然后从第2个记录逐个进行插插入到已入,直至整个序列有序为止。
要点:设立哨兵,作为临时存储和判断数组边界之用。
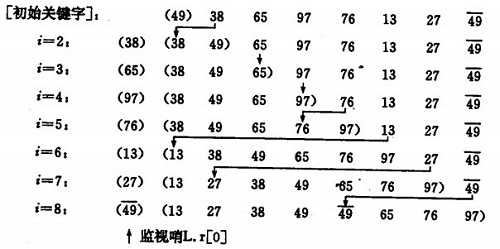
直接插入排序示例:
如果碰见一个和插入元素相等的,那么插入元素把想插入的元素放在相等元素的后面。所以,相等元素的前后顺序没有改变,从原无序序列出去的顺序就是排好序后的顺序,所以插入排序是稳定的。
直接插入排序(straight insertion sort)的做法是:
每次从无序表中取出第一个元素,把它插入到有序表的合适位置,使有序表仍然有序。
第一趟比较前两个数,然后把第二个数按大小插入到有序表中; 第二趟把第三个数据与前两个数从后向前扫描,把第三个数按大小插入到有序表中;依次进行下去,进行了(n-1)趟扫描以后就完成了整个排序过程。
直接插入排序是由两层嵌套循环组成的。外层循环标识并决定待比较的数值。内层循环为待比较数值确定其最终位置。直接插入排序是将待比较的数值与它的前一个数值进行比较,所以外层循环是从第二个数值开始的。当前一数值比待比较数值大的情况下继续循环比较,直到找到比待比较数值小的并将待比较数值置入其后一位置,结束该次循环。
哨兵的作用
算法中引进的附加记录R[0]称监视哨或哨兵(Sentinel)。
哨兵有两个作用:
① 进人查找(插入位置)循环之前,它保存了R[i]的副本,使不致于因记录后移而丢失R[i]的内容;
② 它的主要作用是:在查找循环中"监视"下标变量j是否越界。一旦越界(即j=0),因为R[0].可以和自己比较,循环判定条件不成立使得查找循环结束,从而避免了在该循环内的每一次均要检测j是否越界(即省略了循环判定条件"j>=1")。
注意:
① 实际上,一切为简化边界条件而引入的附加结点(元素)均可称为哨兵。
【例】单链表中的头结点实际上是一个哨兵
② 引入哨兵后使得测试查找循环条件的时间大约减少了一半,所以对于记录数较大的文件节约的时间就相当可观。对于类似于排序这样使用频率非常高的算法,要尽可能地减少其运行时间。所以不能把上述算法中的哨兵视为雕虫小技,而应该深刻理解并掌握这种技巧。
算法的实现:
#include<iostream>using namespace std;int main(){ int a[]={98,76,109,34,67,190,80,12,14,89,1}; int k=sizeof(a)/sizeof(a[0]); int j; for(int i=1;i<k;i++)//循环从第2个元素开始 { if(a[i]<a[i-1]) { int move=a[i]; for(j=i-1;j>=0 && a[j]>move;j--)//a[j]若小于要挪动的数,则是循环终止的条件 { a[j+1]=a[j];//将a[i]前元素向后挪动一个 } a[j+1]=move;//此处就是a[j+1]=move; } } for(int f=0;f<k;f++) { cout<<a[f]<<" "; } return 0;}
效率:
时间复杂度:O(n^2).
其他的插入排序有二分插入排序,2-路插入排序。