python做单因素方差分析

方差分析的主要功能就是验证两组样本，或者两组以上的样本均值是否有显著性差异，即均值是否一样。

这里有两个大点需要注意：①方差分析的原假设是：样本不存在显著性差异（即，均值完全相等）；②两样本数据无交互作用（即，样本数据独立）这一点在双因素方差分析中判断两因素是否独立时用。

原理：

方差分析的原理就一个方程：SST=SS组间+SSR组内  (全部平方和=组间平方和+组内平方和)

说明：方差分析本质上对总变异的解释。

• 组间平方和=每一组的均值减去样本均值
• 组内平方和=个体减去每组平方和

方差分析看的最终结果看的统计量是：F统计量、R²。

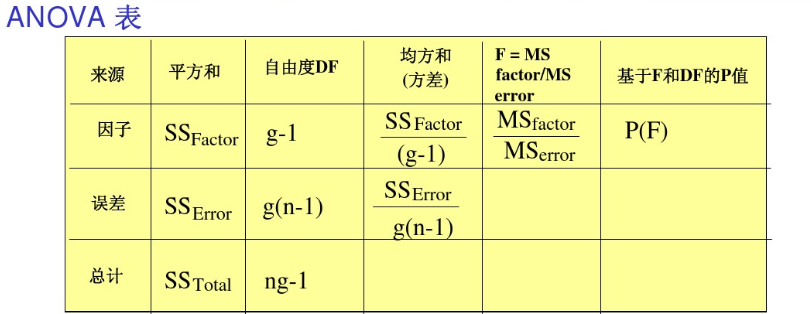
其中：g为组别个数，n为每个组内数据长度。

python实现：

from scipy import stats
from statsmodels.formula.api import ols
from statsmodels.stats.anova import anova_lm
from statsmodels.stats.multicomp import pairwise_tukeyhsd
import warnings
warnings.filterwarnings("ignore")

import itertools

df2=pd.DataFrame()
df2['group']=list(itertools.repeat(-1.,9))+ list(itertools.repeat(0.,9))+list(itertools.repeat(1.,9))

df2['noise_A']=0.0
for i in data['A'].unique():
    df2.loc[df2['group']==i,'noise_A']=data.loc[data['A']==i,['1','2','3']].values.flatten()
    
df2['noise_B']=0.0
for i in data['B'].unique():
    df2.loc[df2['group']==i,'noise_B']=data.loc[data['B']==i,['1','2','3']].values.flatten()  
    
df2['noise_C']=0.0
for i in data['C'].unique():
    df2.loc[df2['group']==i,'noise_C']=data.loc[data['C']==i,['1','2','3']].values.flatten()  
    
df2

# for A
anova_reA= anova_lm(ols('noise_A~C(group)',data=df2[['group','noise_A']]).fit())
print(anova_reA)
#B
anova_reB= anova_lm(ols('noise_B~C(group)',data=df2[['group','noise_B']]).fit())
print(anova_reB)
#C
anova_reC= anova_lm(ols('noise_C~C(group)',data=df2[['group','noise_C']]).fit())
print(anova_reC)

　　从结果可以看出，A、B两样本，在每个组间均值显著无差异，C样本的组间均值是有差异的。