#1445 : 后缀自动机二·重复旋律5
描述
小Hi平时的一大兴趣爱好就是演奏钢琴。我们知道一个音乐旋律被表示为一段数构成的数列。
现在小Hi想知道一部作品中出现了多少不同的旋律?
输入
共一行,包含一个由小写字母构成的字符串。字符串长度不超过 1000000。
输出
一行一个整数,表示答案。
- 样例输入
-
aab
- 样例输出
-
5
解题方法提示
小Hi:本周的题目其实就是给定一个字符串S,要求出S的所有不同子串的数目。小Ho你知道如何快速求解么?
小Ho:我们最近在讨论后缀自动机,所以肯定是和后缀自动机有关!根据上周学习的SAM的基本概念和性质,SAM的每个状态st都包含了一部分S的子串,记作substrings(st),并且(1)对于两个不同状态u和v,包含的子串substrings(u) ∩ substrings(v) = ∅; (2)每个子串都恰好被一个状态包含。所以我们只要构造出来S对应的SAM,再对所有状态st求Σ(maxlen(st)-minlen(st))就是子串的数目。
小Hi:没错。上周我们提到SAM有O(length(S))的构造法。这周我们就来讲一讲如何构造。
小Hi:首先,为了实现O(length(S))的构造,我们对于每个状态不能保存太多数据。例如substring(st)肯定是没法保存下来了。对于状态st我们只保存如下数据:
数据 含义 maxlen[st] st包含的最长子串的长度 minlen[st] st包含的最短字串的长度 trans[st][] st的转移函数 slink[st] st的Suffix Link 小Hi:其次,我们用增量法构造S对应的SAM。我们从初始状态开始,每次添加一个字符S[1], S[2], ... S[N],依次构造可以识别S[1], S[1..2], S[1..3], ... S[1..N]=S的SAM。
小Hi:假设我们已经构造好了S[1..i]的SAM。这时我们要添加字符S[i+1],于是我们新增了i+1个S[i+1]的后缀要识别:S[1..i+1], S[2..i+1], ... S[i..i+1], S[i+1]。 考虑到这些新增状态分别是从S[1..i], S[2..i], S[3..i], ... , S[i], ""(空串)通过字符S[i+1]转移过来的,所以我们还要对S[1..i], S[2..i], S[3..i], ... , S[i], ""(空串)对应的状态们增加相应的转移。
小Hi:我们假设S[1..i]对应的状态是u,等价于S[1..i]∈ substrings(u)。根据上周的讨论我们知道S[1..i], S[2..i], S[3..i], ... , S[i], ""(空串)对应的状态们恰好就是从u到初始状态S的由Suffix Link连接起来路径上的所有状态,不妨称这条路径(上所有状态集合)是suffix-path(u->S)。
小Hi:显然至少S[1..i+1]这个子串不能被以前的SAM识别,所以我们至少需要添加一个状态z,z至少包含S[1..i+1]这个子串。
小Hi:首先考虑一种最简单的情况:对于suffix-path(u->S)的任意状态v,都有trans[v][S[i+1]]=NULL。这时我们只要令trans[v][S[i+1]]=z,并且令slink[st]=S即可。
小Hi:例如我们已经得到"aa"的SAM,现在希望构造"aab"的SAM。如下图所示:
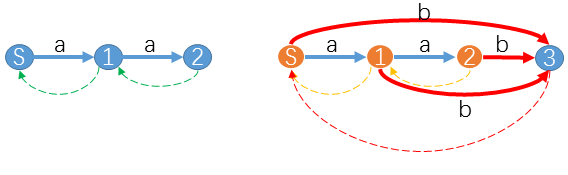
小Hi:此时u=2,z=3,suffix-path(u->S)是桔色状态组成的路径2-1-S。并且这3个状态都没有对应字符b的转移。所以我们只要添加红色转移trans[2][b]=trans[1][b]=trans[S][b]=z即可。当然也不要忘了slink[3]=S。
小Ho:那要是suffix-path(u->S)上有一个节点v,使得trans[v][S[i+1]]!=NULL怎么办?
小Hi:好问题。我们以下图为例,假设我们已经构造"aabb"的SAM如图,现在我们要增加一个字符a构造"aabba"的SAM。
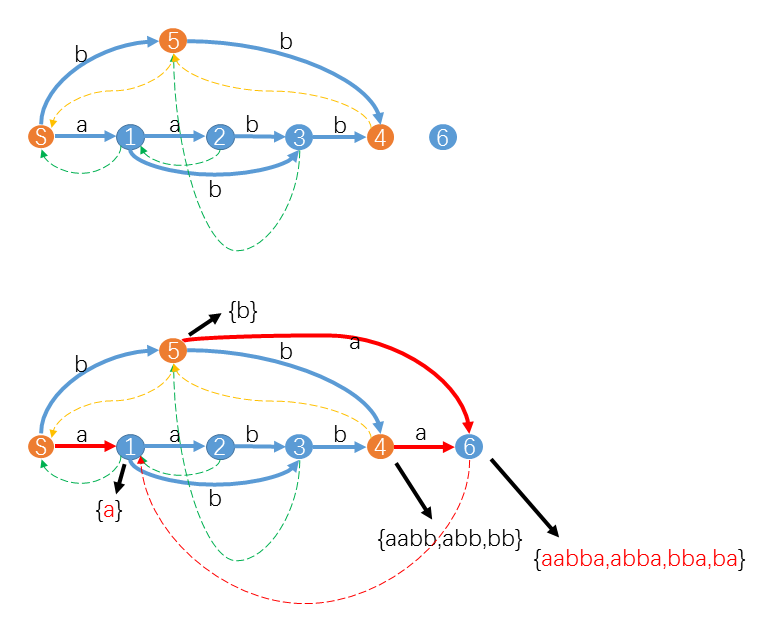
小Hi:这时u=4,z=6,suffix-path(u->S)是桔色状态组成的路径4-5-S。对于状态4和状态5,由于它们都没有对应字符a的转移,所以我们只要添加红色转移trans[4][a]=trans[5][a]=z=6即可。面对S时我们遇到了小Ho你提出的问题,trans[S][a]=1已经存在,怎么办?
小Ho:怎么办呢?
小Hi:不失一般性,我们可以认为在suffix-path(u->S)遇到的第一个状态v满足trans[v][S[i+1]]=x。这时我们需要讨论x包含的子串的情况。如果x中包含的最长子串就是v中包含的最长子串接上字符S[i+1],等价于maxlen(v)+1=maxlen(x),比如在上面的例子里,v=S, x=1,longest(v)是空串,longest(1)="a"就是longest(v)+'a'。这种情况比较简单,我们只要增加slink[z]=x即可。
小Hi:如果x中包含的最长子串 不是 v中包含的最长子串接上字符S[i+1],等价于maxlen(v)+1 < maxlen(x),这种情况最为复杂,不失一般性,我们用下图表示这种情况,这时增加的字符是c,状态是z。

小Hi:在suffix-path(u->S)这条路径上,从u开始有一部分连续的状态满足trans[u..][c]=NULL,对于这部分状态我们只需增加trans[u..][c]=z。紧接着有一部分连续的状态v..w满足trans[v..w][c]=x,并且longest(v)+c不等于longest(x)。这时我们需要从x拆分出新的状态y,并且把原来x中长度小于等于longest(v)+c的子串分给y,其余字串留给x。同时令trans[v..w][c]=y,slink[y]=slink[x], slink[x]=slink[z]=y。
小Ho:好像比较复杂。
小Hi:我们来举个例子。假设我们已经构造"aab"的SAM如图,现在我们要增加一个字符b构造"aabb"的SAM。
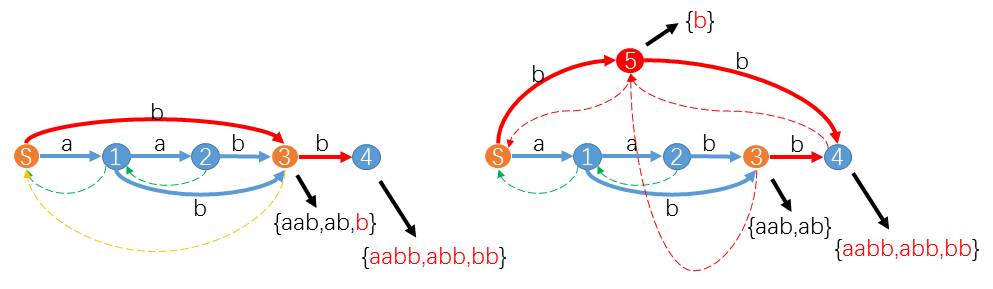
小Hi:当我们处理在suffix-path(u->S)上的状态S时,遇到trans[S][b]=3。并且longest(3)="aab",longest(S)+'b'="b",两者不相等。其实不相等意味增加了新字符后endpos("aab")已经不等于endpos("b"),势必这两个子串不能同属一个状态3。这时我们就要从3中新拆分出一个状态5,把"b"及其后缀分给5,其余的子串留给3。同时令trans[S][c]=5, slink[5]=slink[3]=S, slink[3]=slink[6]=5。
小Hi:整个过程的代码如下,其中状态0代表初始状态S;状态u, v, x, y, z的意义如上文所述;-1代表slink或者trans不存在。
const int MAXL = 1000000; string s; int n = 0, len, st; int maxlen[2 * MAXL + 10], minlen[2 * MAXL + 10], trans[2 * MAXL + 10][26], slink[2 * MAXL + 10]; int new_state(int _maxlen, int _minlen, int* _trans, int _slink) { maxlen[n] = _maxlen; minlen[n] = _minlen; for(int i = 0; i < 26; i++) { if(_trans == NULL) trans[n][i] = -1; else trans[n][i] = _trans[i]; } slink[n] = _slink; return n++; } int add_char(char ch, int u) { int c = ch - 'a'; int z = new_state(maxlen[u] + 1, -1, NULL, -1); int v = u; while(v != -1 && trans[v][c] == -1) { trans[v][c] = z; v = slink[v]; } if(v == -1) { //最简单的情况,suffix-path(u->S)上都没有对应字符ch的转移 minlen[z] = 1; slink[z] = 0; return z; } int x = trans[v][c]; if(maxlen[v] + 1 == maxlen[x]) { //较简单的情况,不用拆分x minlen[z] = maxlen[x] + 1; slink[z] = x; return z; } int y = new_state(maxlen[v] + 1, -1, trans[x], slink[x]); //最复杂的情况,拆分x slink[y] = slink[x]; minlen[x] = maxlen[y] + 1; slink[x] = y; minlen[z] = maxlen[y] + 1; slink[z] = y; int w = v; while(w != -1 && trans[w][c] == x) { trans[w][c] = y; w = slink[w]; } minlen[y] = maxlen[slink[y]] + 1; return z; }小Ho:咦?程序倒是意外的简单。
#include <iostream> #include <cstring> #include <cstdio> #include <cstring> #include <algorithm> #include <cmath> #include <time.h> #include <string> #include <map> #include <stack> #include <vector> #include <set> #include <queue> using namespace std; typedef long long ll; const int inf=0x3f3f3f3f; const int N=1e6+100; const int M=1e6+5; int tot,slink[2*N],trans[2*N][26],minlen[2*N],maxlen[2*N]; char str[N]; int n; int newstate(int _maxlen,int _minlen,int* _trans,int _slink) { maxlen[++tot]=_maxlen; minlen[tot]=_minlen; slink[tot]=_slink; if(_trans) for(int i=0; i<26; i++) trans[tot][i]=_trans[i]; return tot; } int add_char(char ch,int u) { int c=ch-'a',v=u; int z=newstate(maxlen[u]+1,-1,NULL,0); while(v&&!trans[v][c]) { trans[v][c]=z; v=slink[v]; } if(!v) { minlen[z]=1; slink[z]=1; return z; } int x=trans[v][c]; if(maxlen[v]+1==maxlen[x]) { slink[z]=x; minlen[z]=maxlen[x]+1; return z; } int y=newstate(maxlen[v]+1,-1,trans[x],slink[x]); slink[z]=slink[x]=y; minlen[x]=minlen[z]=maxlen[y]+1; while(v&&trans[v][c]==x) { trans[v][c]=y; v=slink[v]; } minlen[y]=maxlen[slink[y]]+1; return z; } int main() { scanf("%s",str); int len=strlen(str),pre=1; tot=1; for(int i=0; i<len; i++) { pre=add_char(str[i],pre); } long long ans=0; for(int i=2; i<=tot; i++) { ans+=maxlen[i]-minlen[i]+1; } cout<<ans<<endl; return 0; }